Cho bảng số liệu thống kê điểm kiểm tra 1 tiết môn Toán của 40 học sinh như sau: tính số trung vị
tính số trung vị
BH
Những câu hỏi liên quan
Số liệu thống kê điểm kiểm tra môn Toán của học sinh lớp 10A được cho trong bảng sau:Đơn vị điều tra và kích thước mẫu của bảng số liệu trên là: A. Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A. Kích thước mẫu của số liệu: 44 B. Đơn vị điều tra: Điểm trung bình môn Toán của lớp 10A. Kích thước mẫu của số liệu: 45 C. Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A. Kích thước mẫu của số liệu: 45 D. Đơn vị điều tra: Điểm trung bình môn Toán của lớp 10A. Kích thước mẫu của số liệu: 44
Đọc tiếp
Số liệu thống kê điểm kiểm tra môn Toán của học sinh lớp 10A được cho trong bảng sau:
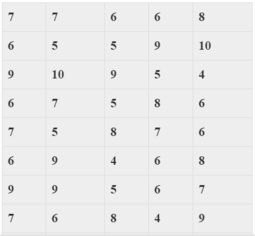

Đơn vị điều tra và kích thước mẫu của bảng số liệu trên là:
A. Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A. Kích thước mẫu của số liệu: 44
B. Đơn vị điều tra: Điểm trung bình môn Toán của lớp 10A. Kích thước mẫu của số liệu: 45
C. Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A. Kích thước mẫu của số liệu: 45
D. Đơn vị điều tra: Điểm trung bình môn Toán của lớp 10A. Kích thước mẫu của số liệu: 44
Chọn A.
Đơn vị điều tra: Điểm kiểm tra môn Toán của lớp 10A
Liệt kê số điểm của 44 học sinh lớp 10A nên kích thước mẫu của số liệu là 44.
Đúng 0
Bình luận (0)
Thống kê điểm kiểm tra môn Toán của một lớp 10 có 22 học sinh nữ và 20 học sinh nam được cho ở bảng sau: Cho biết đơn vị điều tra và kích thước của mẫu số liệu trên? A. Đơn vị điều tra: môn Toán, kích thước của mẫu số liệu: 42 B. Đơn vị điều tra: môn Toán, kích thước của mẫu số liệu: 22 C. Đơn vị điều tra: một học sinh lớp 10, kích thước của mẫu số liệu: 20 D. Đơn vị điều tra: một học sinh lớp 10, kích thước của mẫu số liệu: 42
Đọc tiếp
Thống kê điểm kiểm tra môn Toán của một lớp 10 có 22 học sinh nữ và 20 học sinh nam được cho ở bảng sau:

Cho biết đơn vị điều tra và kích thước của mẫu số liệu trên?
A. Đơn vị điều tra: môn Toán, kích thước của mẫu số liệu: 42
B. Đơn vị điều tra: môn Toán, kích thước của mẫu số liệu: 22
C. Đơn vị điều tra: một học sinh lớp 10, kích thước của mẫu số liệu: 20
D. Đơn vị điều tra: một học sinh lớp 10, kích thước của mẫu số liệu: 42
Đơn vị điều tra: một hsinh lớp 10.
Do lớp học có 22 nữ và 20 nam nên lớp có tất cả 42 học sinh . Do đó; kích thước của mẫu số liệu: 42
Chọn D
Đúng 0
Bình luận (0)
Bài 1: Điểm kiểm tra môn toán học kỳ 2 của học sinh lớp 7A được thống kê như sau:10910999899109101078108989981088979109a/ Dấu hiệu ở đây là gì ? có bao nhiêu giá trị của dấu hiệu ? b/ Lập bảng tần số và rút ra nhận xét.c/ Tính số trung bình cộng của dấu hiệu. Tìm mốt của dấu hiệu? d/ Vẽ biểu đồ đoạn thẳng.Bài 2 : Lớp 7A góp tiền ủng hộ đồng bào bị thiên tai. Số tiền góp của mỗi bạn được thống kê trong bảng ( đơn vị là nghìn đồng) a. Dấu hiệu ở đây là gì?b. Lập bảng “tần số”, tính t...
Đọc tiếp
Bài 1: Điểm kiểm tra môn toán học kỳ 2 của học sinh lớp 7A được thống kê như sau:
10 | 9 | 10 | 9 | 9 | 9 | 8 | 9 | 9 | 10 |
9 | 10 | 10 | 7 | 8 | 10 | 8 | 9 | 8 | 9 |
9 | 8 | 10 | 8 | 8 | 9 | 7 | 9 | 10 | 9 |
a/ Dấu hiệu ở đây là gì ? có bao nhiêu giá trị của dấu hiệu ?
b/ Lập bảng tần số và rút ra nhận xét.
c/ Tính số trung bình cộng của dấu hiệu. Tìm mốt của dấu hiệu?
d/ Vẽ biểu đồ đoạn thẳng.
Bài 2 : Lớp 7A góp tiền ủng hộ đồng bào bị thiên tai. Số tiền góp của mỗi bạn được thống kê trong bảng ( đơn vị là nghìn đồng)
 |
a. Dấu hiệu ở đây là gì?
b. Lập bảng “tần số”, tính trung bình cộng
........................................................ Chương 4 – ĐƠN THỨC, ĐA THỨC
Bài 1: Cặp đơn thức nào sau đây đồng dạng:
a) 3 và
- 0,5
b) 2xy3 và 2 x3y c) 5xy2 và 7y2x d)
2xy2 z và
-0,7xyzy
Bài 2: Biểu thức nào là đơn thức :13x2 y + x; 3 - 2x;
- 5x; 3( x + y ); 3xy2 ;
2x ; 7
![]() y
y
Bài 3: Thu gọn đơn thức , xác định phần hệ số và phần biến. Tìm bậc đơn thức?
![]() a) ( -2xy2 )3.(-3xy) b) (-3xy2)2. 1 xy c) (-2x).(-0.5xyz)
a) ( -2xy2 )3.(-3xy) b) (-3xy2)2. 1 xy c) (-2x).(-0.5xyz)
9
Bài 4: Tìm nghiệm các đa thức
a) 2x – 4 b) 4x + 3 c) x2 – 2x d) 2x2 – 18 e*) x2 + 1
Bài 5: Cho đa thức M(x) = 5x3 – x2 + 4x + 2x2 - 5x3 + 4
a) Thu gọn, sắp xếp giảm dần theo biến, tìm bậc của đa thức thu được.
b) Tính giá trị của đa thức M(x) tại x= 5; x= -2; x= -4
Bài 6: Cho hai đa thức A(x)= x3+3x2- 4x+5; B(x) = x3-2x2+x+3
a) Tính : A(1); A(-2) ; B (-3) b) Tính A(x) - B(x) c) Tính A(x) + B(x)
![]() Bài 7: Rút gọn rồi tính giá trị biểu thức A = 2x2y – 3xy2 – x2y + 2xy2 –xy + 1 tại x = -2; y = 1
Bài 7: Rút gọn rồi tính giá trị biểu thức A = 2x2y – 3xy2 – x2y + 2xy2 –xy + 1 tại x = -2; y = 1
2
Bài 8: Cho hai đa thức P(x) = 2x3 – 2x + x2 – x3 + 3x + 2
và Q(x) = 3x3 - 4x2 + 3x – 4x – 4x3 + 5x2 + 1
a) Thu gọn và sắp xếp các đa thức theo lũy thừa giảm dần của biến .
b) Tính M(x) = P(x) + Q(x) ; N(x) = P(x) – Q(x)
c) Chứng tỏ đa thức M(x) không có nghiệm ( vô nghiệm)
Bài 9: Tìm đa thức M biết:
a) M – (3xy – 4y2) = x2 – 7xy + 8y2
b) M + (5x2 – 2xy) = 6x2 + 9xy – y2
c) (9xy – 7x2y + 1) – M = (3 – 2x2y – 3xy)
Bài 10: Cho đa thức M(x) = 4x3 + 2x4 – x2 – x3 + 2x2 – x4 + 1 – 3x3
a) Thu gọn và sắp xếp đa thức trên theo luỹ thừa giảm dần của biến.
b) Tính M(–1) và M(1)
c) *Chứng tỏ đa thức trên không có nghiệm
Bài 11: Cho các đa thức: f(x) = x3 – 2x2 + 3x + 1; g(x) = x3 + x – 1; h(x) = 2x2 – 1
a) Tính: f(x) – g(x) + h(x)
b) Tìm x sao cho f(x) – g(x) + h(x) = 0
Bài 12: Cho f(x) = (x – 4) – 3(x + 1). Tìm x sao cho f(x) = 4.
Bài 13: Cho các đa thức: A = x2 – 2x – y2 + 3y – 1 ; B = – 2x2 + 3y2 – 5x + y + 3 Tìm đa thức C biết:
a) C = A+ B b) C + B = A c) B – C = A
Bài 14: Tìm hệ số m để đa thức mx 2 – 4x +5 có x = – 1 là một nghiệm
Phần hình học
Bài 1: Cho tam giác ABC có ![]() = 400 ;
= 400 ; ![]() = 600. So sánh độ dài AB và BC.
= 600. So sánh độ dài AB và BC.
![]() Bài 2: Cho ABC có AB = 5cm, BC = 7cm, AC = 6cm. So sánh các góc của tam giác ABC.
Bài 2: Cho ABC có AB = 5cm, BC = 7cm, AC = 6cm. So sánh các góc của tam giác ABC.
![]() Bài 3: Cho ABC = ∆ DEF; viết tất cả các cặp cạnh, cặp góc bằng nhau của hai tam giác đã cho.
Bài 3: Cho ABC = ∆ DEF; viết tất cả các cặp cạnh, cặp góc bằng nhau của hai tam giác đã cho.
Bài 4:Cho tam giác DMN vuông tại D có DM = 6dm; MN = 10 dm. Tính DN.
Bài 5: Cho tam giác ABC với BC = 1cm, AC = 9cm . Tìm độ dài cạnh AB, biết độ dài này là một số nguyên (cm).
Bài 6: Cho tam giác ABC cân, biết AB = 5,2 cm; BC = 1,2 cm. Tính độ dài cạnh AC. (Không cần vẽ hình)
Bài 7: Cho tam giác ABC (hình5) có AH vuông góc với BC (H thuộc BC)
a) Biết ![]() , hãy so sánh HB và HC .
, hãy so sánh HB và HC .
b)  Biết HB < HC, hãy so sánh
Biết HB < HC, hãy so sánh ![]()
Bài 8: Cho ∆ABC cân tại A. Trên cạnh AB lấy điểm D, trên cạnh AC lấy điểm E sao cho AD = AE.
a) Chứng minh: ∆ ABE = ∆ ACD
b) Gọi I là giao điểm của BE và CD. Chứng minh AI là tia phân giác của góc BAC. Bài 9: Cho tam giác DEF cân tại D có DE = DF = 17cm, EF = 16cm, đường trung tuyến DM. Chứng minh:
a) ∆DEM = ∆DFM.
b) Tính DM.
c)* Gọi G là trọng tâm của tam giác DEF. Tính GD, GM.
Bài 10: Cho ∆DEM cân tại D có hai đường trung tuyến MA và EB cắt nhau tại C (A thuộc DE,
B thuộc DM). Chứng minh rằng
a) ∆DEB = ∆DMA b) *ME < 4AC
Bài 11: Cho ∆ABC cân tại A, kẻ AH vuông góc với BC (H ∊ BC).
a) Chứng minh: ∆ABH = ∆ACH
b) Gọi K là trung điểm AC, BK cắt AH tại G. Tính GH biết AH = 9cm.
Bài 12: Cho tam giác ABC cân tại A, đường cao AH. Biết AB = 10cm, BC = 12cm.
a) Chứng minh ΔABH = ΔACH.
b) Tính độ dài đoạn thẳng AH.
c) *Gọi G là trọng tâm của tam giác ABC. Chứng minh ba điểm A, G, H thẳng hàng. Bài 13: Cho tam giác ABC vuông tại B, vẽ trung tuyến AM, trên tia đối của tia MA lấy điểm E sao cho ME = MA. Chứng minh:
a) ∆ABM = ∆ECM b) EC ⟘ BC c)* AC > CE d) *BE//AC
Bài 14: Cho tam giác ABC cân tại A, kẻ BH vuông góc với AC và CK vuông góc với AB (H thuộc AC; K thuộc AB)
a) Chứng minh BH = CK
b) Gọi I là giao điểm của BH và CK. Tam giác IBC là tam giác gì? Vì sao?
c) *Chứng minh I nằm trên tia phân giác của góc BAC
Bài 15: Cho tam giác ABC, gọi M là trung điểm của AB. Trên tia đối của tia MC lấy điểm D sao cho MD = MC. Chứng minh: a) AC = DB b) *AC + BC > 2AM.
Bài 16: Cho ![]() = 600, Ot là tia phân giác của góc xOy, lấy điểm C thuộc Ot ( C ≠ O)
= 600, Ot là tia phân giác của góc xOy, lấy điểm C thuộc Ot ( C ≠ O)
![]()
![]() Từ C kẻ CA vuông góc Ox ( A Ox), kẻ CB vuông góc Oy ( B Oy). Chứng minh rằng:
Từ C kẻ CA vuông góc Ox ( A Ox), kẻ CB vuông góc Oy ( B Oy). Chứng minh rằng:
a) Tam giác OAB đều. b) OC là đường trung trực của AB.
Bài 17: Cho tam giác cân ABC cn tại A. Kẻ AH vuông góc với BC (H ∊ BC).
a) Chứng minh HB = HC.
b) Cho biết AB = AC = 5cm, BC = 6cm. Tính độ dài AH.
c) *Kẻ HE vuông góc với AB (E ∊ AB), kẻ HF vuông góc với AC (F ∊AC). Chứng minh tam giác EFH là tam giác cân.
Bài 18: Cho tam giác ABC (AB <AC), có AD là tia phân giác của góc A (D∊BC). Trên tia AC lấy điểm E sao cho AE = AB.
a) Chứng minh: BD = DE
b) Gọi K là giao điểm của các đường thẳng AB và ED. Chứng minh: ∆ ABC = ∆AEK và
c) ∆AKC là tam giác gì? Vì sao?
d) *Chứng minh: AD ⟘ KC.
Bài 19: Cho tam giác nhọn ABC. Vẽ ra phía ngoài tam giác ABC các tam giác đều ABD và ACE. Gọi M là giao điểm của DC và BE. Chứng minh rằng:
a) ∆ABE ∆ADC
b) BMC = 1200
Bài 20: Cho ∆ABC cân tại A và hai đường trung tuyến BM, CN cắt nhau tại K
a) Chứng minh ∆BNC = ∆CMB
b) Chứng minh ∆BKC cân tại K
c) Chứng minh BC < 4.KM
Bài 1 Điểm kiểm tra môn toán học kỳ 2 của học sinh lớp 7A được thống kê như sau.10910999899109101078108989981088979109a) Dấu hiệu ở đây là gì ? có bao nhiêu giá trị của dấu hiệu ?b) Lập bảng tần số.c) Tính số trung bình cộng của dấu hiệu
Đọc tiếp
Bài 1 Điểm kiểm tra môn toán học kỳ 2 của học sinh lớp 7A được thống kê như sau.
| 10 | 9 | 10 | 9 | 9 | 9 | 8 | 9 | 9 | 10 |
| 9 | 10 | 10 | 7 | 8 | 10 | 8 | 9 | 8 | 9 |
| 9 | 8 | 10 | 8 | 8 | 9 | 7 | 9 | 10 | 9 |
a) Dấu hiệu ở đây là gì ? có bao nhiêu giá trị của dấu hiệu ?
b) Lập bảng tần số.
c) Tính số trung bình cộng của dấu hiệu
a, Dấu hiệu: điểm kiểm tra môn toán học kỳ 2 của học sinh lớp 7A
Có 30 giá trị
b, Bảng tần số:
| Giá trị (x) | 7 | 8 | 9 | 10 | |
| Tần số (n) | 2 | 7 | 13 | 8 | N=30 |
c, \(\overline{N}=\dfrac{7.2+8.7+9.13+10.8}{30}=8,9\)
Đúng 1
Bình luận (0)
a. Dấu hiệu ơ đây là điểm kiểm tra toán học kì 2 của mỗi học sinh lớp 7A. Có 30 giá trị của dấu hiệu
b.
| Giá trị ( x ) | Tần số ( n) |
| 10 | 8 |
| 9 | 13 |
| 8 | 7 |
| 7 | 2 |
| N = 30 |
c.
\(X=\dfrac{10.8+9.13+8.7+7.2}{30}=\dfrac{267}{30}=8,9\)
Vậy điểm trung bình điểm kiểm tra toán học kì 2 của lớp 7A là 8,9 điểm
Đúng 0
Bình luận (0)
Bài 1. Điểm kiểm tra môn toán lớp 7A được thống kê như sau7105781065785641034989947392375975764958563Lập bảng tần số có giá trị trung bình cộng. Vẽ biểu đồ đoạn thẳng, nhận xét về việc học toán của học sinh lớp 7A
Đọc tiếp
Bài 1. Điểm kiểm tra môn toán lớp 7A được thống kê như sau
7 | 10 | 5 | 7 | 8 | 10 | 6 | 5 | 7 | 8 |
5 | 6 | 4 | 10 | 3 | 4 | 9 | 8 | 9 | 9 |
4 | 7 | 3 | 9 | 2 | 3 | 7 | 5 | 9 | 7 |
5 | 7 | 6 | 4 | 9 | 5 | 8 | 5 | 6 | 3 |
Lập bảng tần số có giá trị trung bình cộng. Vẽ biểu đồ đoạn thẳng, nhận xét về việc học toán của học sinh lớp 7A
điểm kiểm tra môn toán của học sinh lớp 6 được ghi như sau: 96285747257589686586787749295
a) nêu đối tượng thống kê và tiêu chí thống kê
b) lập bảng thống kê
c) học sinh trung bình (trên 5 điểm ) chiếm bao nhiêu % học sinh cả lớp
Em ơi chắc em copy đề ở đâu qua à nhưng giá trị kiểu kia không ai hiểu mà giúp em được rồi.
Đúng 8
Bình luận (0)
Giá trị gì kì vậy :))
Với lại có biết số hs của lớp đó đâu mà tính câu C :/
Đúng 2
Bình luận (0)
điểm kiểm tra môn toán của học sinh lớp 6 được ghi như sau : 96285747257589686586787749295
a) nêu đối tượng thống kê và tiêu chí thống kê
b) lập bảng thống kê
c) học sinh trung bình (trên 5 điểm ) chiếm bao nhiêu % học sinh cả lớp
a. Đối tượng thống kê là điểm kiểm tra môn toán của học sinh lớp 6
b. bảng thống kê
| Điểm | 2 | 4 | 5 | 6 | 7 | 8 | 9 |
| tần số | 3 | 2 | 5 | 4 | 6 | 5 | 4 |
c. Tổng số học sinh là 29 học sinh
số học sinh có điểm trên 5 là : 19 chiếm \(\frac{19}{29}\times100\%=65.5\%\)
Trong đợt kiểm tra học kì 1 môn Toán năm học 2021-2022 sau khi thống kê với 40 học sinh lớp 6A3 người ta thấy số học sinh đạt các điểm: Giỏi, khá, trung bình lần lượt bằng tổng số học sinh của lớp 6A3. Còn lại là học sinh bị điểm Yếu. Tính số học sinh đạt điểm giỏi, Khá, trung bình, yếu của lớp 6A3 trong đợt kiểm tra học kì 1 môn Toán, năm học 2021-2022.
Đọc tiếp
Trong đợt kiểm tra học kì 1 môn Toán năm học 2021-2022 sau khi thống kê với 40 học sinh lớp 6A3 người ta thấy số học sinh đạt các điểm: Giỏi, khá, trung bình lần lượt bằng ![]() tổng số học sinh của lớp 6A3. Còn lại là học sinh bị điểm Yếu. Tính số học sinh đạt điểm giỏi, Khá, trung bình, yếu của lớp 6A3 trong đợt kiểm tra học kì 1 môn Toán, năm học 2021-2022.
tổng số học sinh của lớp 6A3. Còn lại là học sinh bị điểm Yếu. Tính số học sinh đạt điểm giỏi, Khá, trung bình, yếu của lớp 6A3 trong đợt kiểm tra học kì 1 môn Toán, năm học 2021-2022.
Trong đợt kiểm tra học kì 1 môn Toán năm học 2021-2022 sau khi thống kê với 40 học sinh lớp 6A3 người ta thấy số học sinh đạt các điểm: Giỏi, khá, trung bình lần lượt bằng , , tổng số học sinh của lớp 6A3. Còn lại là học sinh bị điểm Yếu. Tính số học sinh đạt điểm giỏi, Khá, trung bình, yếu của lớp 6A3 trong đợt kiểm tra học kì 1 môn Toán, năm học 2021-2022.
Đọc tiếp
Trong đợt kiểm tra học kì 1 môn Toán năm học 2021-2022 sau khi thống kê với 40 học sinh lớp 6A3 người ta thấy số học sinh đạt các điểm: Giỏi, khá, trung bình lần lượt bằng ![]() ,
, ![]() ,
, ![]() tổng số học sinh của lớp 6A3. Còn lại là học sinh bị điểm Yếu. Tính số học sinh đạt điểm giỏi, Khá, trung bình, yếu của lớp 6A3 trong đợt kiểm tra học kì 1 môn Toán, năm học 2021-2022.
tổng số học sinh của lớp 6A3. Còn lại là học sinh bị điểm Yếu. Tính số học sinh đạt điểm giỏi, Khá, trung bình, yếu của lớp 6A3 trong đợt kiểm tra học kì 1 môn Toán, năm học 2021-2022.



