Tìm n thuộc Z để (2n2+6-1) chia hết cho n-1
Làm ơn giải hộ mình nha!!! Mình ngu toán lắm T-T
Tìm x thuộc Z để (2x+7) chia hết cho (x+1)
Các bạn giải cụ thể giùm mình nha. Mình cần gấp lắm, help me!
2x + 7 chia hết cho x + 1
=> 2x + 2 + 5 chia hết cho x + 1
=> 2.(x + 1) + 5 chia hết cho x + 1
mà 2.(x + 1) chia hết cho x + 1
=> 5 chia hết cho x + 1
=> x + 1 thuộc Ư(5) = {-5; -1; 1; 5}
=> x thuộc {-6; -2; 0; 4}.
Ta có 2x+7 = 2x +2 +5
Để 2x+7 chia hết cho x+1 thì 5 chia hết cho x+1
=> x+1 thuộc Ư(5) = { -5 ; -1 ; 1 ;5 }
Ta có bảng sau :
| x +1 | -5 | -1 | 1 | 5 |
| x | -6 | -2 | 0 | 4 |
Vậy x = { -6 ; -2 ; 0 ; 4 } thì 2x+7 chia hết cho x+1
Tìm n thuộc z để đa thức (2n^2 + n - 7) chia hết ( n - 2)
giải chi tiết giùm mình nha mình like cho nhanh lên
ta có : 2n^2 +n-7 chia hết cho n- 2
(2n^2 +n-7)-4n(n-2) chia hết cho n-2
2n^2+n-7 - 2n^ 2 -4 chia hết cho n-2
n-7 - 4 chia hết cho n-2
n-2-9 chia hết cho n-2
=> -9 chia hết cho n-2
=> n-2= -1;1;-3;3;-9;9
=> n= 1;3;-1;5;-7;11
Giúp Mình giải bài Toán này với !!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!
Tìm n Thuộc Z
a, (n+1) chia hết cho (n-3)
b, (2n+5) chia hết cho (n+1)
c, 10n chia hết ch (5n-3)
a) n + 1 chia hết cho n - 3
=> n - 3+ 4 chia hết cho n - 3
=> 4 chia hết cho n-3
=> n - 3 thuộc Ư(4) = {1;-1;2;-2;4;-4}
thế n-3 vô từng trường hợp các ước của 4 rồi tim x
b) 2n + 5 chia hết cho n + 1
=> 2n + 2 + 3 chia hết cho n + 1
=> 2(n+1) + 3 chia hết cho n +1
=> 3 chia hết cho n + 1
=> n + 1 thuộc Ư(3) = {1;-1;3;-3}
tìm x giống bài a
c) 10n chia hết cho 5n - 3
=> 10n - 6 + 6 chia hết cho 5n - 3
=> 2.(5n - 3) + 6 chia hết cho 5n - 3
=> 6 chia hết cho 5n - 3
=> 5n - 3 thuộc Ư(6) = {1;-1;2;-2;3;-3;6;-6}
tìm x giống bài a
a. n+1=(n-3)+4
(n+1) chia hết cho (n-3) thì (n-3)+4 chia hết cho (n-3)
Ta có (n-3) chia hết cho (n-3)
Suy ra 4 phải chia hết cho (n-3)
Vậy n= -1 ,1 , 2 , 4
b. 2n+5=2n+2+3=2(n+1)+3
tương tự câu a ta có 2(n+1) chia hết cho (n+1)
Suy ra 3 phải chia hết cho (n+1)
Vậy n=-2,0,2
c.10n=10n-6+6=2(5n-3) +6
Tiếp tục àm tương tự như câu a và b
Tìm x thuộc N,biết:
a) (x+3) chia hết cho (x-1)
b) (4x+3) chia hết cho (2x+1)
Các bạn giải nhanh mình cần gấp để thi học kỳ I môn Toán !
Ai giải hai bài này rùi thì mình xin cảm ơn !
Phần a ,
x + 3 chia hết cho x + 1
x - 1 chia hết cho x - 1
\(\Rightarrow x+3-\left(x-1\right)=4\text{ }⋮\text{ }x-1\)
\(x-1\in\left\{1\text{ };\text{ }-1\text{ };\text{ }2\text{ };\text{ }-2\text{ };\text{ }4\text{ };\text{ }-4\right\}\)
\(\Rightarrow x\in\left\{2\text{ };\text{ }0\text{ };\text{ }3\text{ };\text{ }-1\text{ };\text{ }5\text{ };\text{ }-3\right\}\)
Phần b,
\(\frac{4x+3}{2x+1}=\frac{2\left(2x+1\right)+1}{2x+1}=\frac{2\left(2x+1\right)}{2x+1}+\frac{1}{2x+1}=2+\frac{1}{2x+1}\in Z\)
\(\Rightarrow1\text{ }⋮\text{ }2x+1\)
\(\Rightarrow2x+1\in\left\{1\text{ };\text{ }-1\right\}\)
\(\Rightarrow x=0\)vì \(x\in N\)
Cảm ơn bạn Nguyễn Thị Thu Thủy rất nhiều !
Tìm các số nguyên n để 2n - 4 chia hết cho 2n + 1
Làm giúp mình nhé các bạn ơi
\(2n-4⋮2n+1\)
\(\Rightarrow2n+1-5⋮2n+1\)
=> \(5⋮2n+1\)
=> \(2n+1\inƯ\left(5\right)=\left\{1;-1;5;-5\right\}\)
=> \(2n\in\left\{0;-2;4;-6\right\}\)
=> \(n\in\left\{0;-1;2;-3\right\}\) (TM)
Tìm n thuộc Z+ để 1.2.3.....(n-1) chia hết cho n
Giúp mình nha sáng mai mình nộp r
bài 1 : tìm n thuộc Z sao cho
a) ( n+8) chia hết ( n +3 )
b) ( 2n - 5 ) chia hết ( n - 3)
c ) ( n + 5 ) chia hết ( n - 2 )
d ) ( n + 9) chia hết ( n + 3 )
các cậu giải nhanh cho mình nhé ak mà giải thì giải rõ ràng đừng giải tóm tắt mình khó hiểu lắm
a, n+ 8 chia hết cho n + 3
=> n+ 8 -( n+3) chia hết cho n+ 3
=> 5 chia hết cho n+3
=> n+3 thuộc ước của 5
......
đến đây cậu tự tìm n nhé
b, 2n - 5 chia hết cho n-3
=> 2n -5 - 2n + 6 chia hết cho n- 3 ( nhân n-3 với 2 )
=> 1 chia hết cho n- 3
=> n-3 thuộc ước của 1
....
c,d làm tương tự nhé
Tìm n thuộc N thỏa mãn (2n-1) chia hết cho (n-5)
Trình bày cách giải ra hộ mình nha thanks
Tìm n ∈ Z để 2n2 – n + 2 chia hết cho 2n + 1.
Cách 1: Thực hiện phép chia 2n2 – n + 2 cho 2n + 1 ta có:
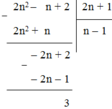
2n2 – n + 2 chia hết cho 2n + 1
⇔ 3 ⋮ (2n + 1) hay (2n + 1) ∈ Ư(3)
⇔ 2n + 1 ∈ {±1; ±3}
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Cách 2:
Ta có:
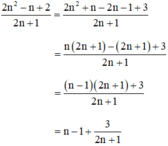
2n2 – n + 2 chia hết cho 2n + 1
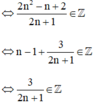
⇔ 2n + 1 ∈ Ư(3) = {±1; ± 3}.
+ 2n + 1 = 1 ⇔ 2n = 0 ⇔ n = 0
+ 2n + 1 = -1 ⇔ 2n = -2 ⇔ n = -1
+ 2n + 1 = 3 ⇔ 2n = 2 ⇔ n = 1
+ 2n + 1 = -3 ⇔ 2n = -4 ⇔ n = -2.
Vậy n ∈ {-2; -1; 0; 1.}
Chú ý: Đa thức A chia hết cho đa thức B khi phần dư của phép chia bằng 0.