\(\Leftrightarrow x^6-2\left(x^3+3x^2+3x+1\right)-15< 0\)

\(\Leftrightarrow x^6-2\left(x+1\right)^3-15< 0\)

\(\Leftrightarrow x^6< 2\left(x+1\right)^3+15\) (1)

- Với \(x\le-2\Rightarrow x+1\le-1\Rightarrow2\left(x+1\right)^3+15\le13\)

Trong khi đó \(x^6\ge2^6=32>13\) (ktm(1))

\(\Rightarrow\) Không tồn tại \(x\le-2\) thỏa mãn BPT (2)

- Với \(x\ge3\Rightarrow x^2\ge3x=2x+x\ge2x+3>2x+2\)

\(\Rightarrow x^2>2\left(x+1\right)\Rightarrow x^6>2^3.\left(x+1\right)^3=8\left(x+1\right)^3\) (3)

(1);(3) \(\Rightarrow2\left(x+1\right)^3+15>8\left(x+1\right)^3\)

\(\Rightarrow6\left(x+1\right)^3< 15\Rightarrow\left(x+1\right)^3< \dfrac{5}{2}< 8\)

\(\Rightarrow x+1< 2\Rightarrow x< 1\) (mâu thuẫn giả thiết \(x\ge3\))

\(\Rightarrow\) Không tồn tại \(x\ge3\) thỏa mãn BPT (4)

Từ (2);(4) \(\Rightarrow\) các giá trị nguyên của x nếu có thỏa mãn BPT chúng sẽ thuộc \(-2< x< 3\)

\(\Rightarrow x=\left\{-1;0;1;2\right\}\)

Thay vào BPT ban đầu thử thấy đều thỏa mãn

Vậy \(x=\left\{-1;0;1;2\right\}\)

Đáp án C.

⇒ Chia 2 vế phương trình cho x 3  ta được:

x 3 + 1 x 3 + 3 x 2 + 1 x 2 + 6 x + 1 x = m   (*)

Đặt t = x + 1 x ⇒ t ≥ 2 , phương trình (*) m = t 3 + 3 t 2 + t - 6  

Xét f ( t ) = t 3 + 3 t 2 + 3 t - 6 trên  ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )

f ' ( t ) = 0 ⇔ t = - 1  

Bảng biến thiên:

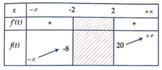
⇒ f ( t ) ∈ ( - ∞ ; - 8 ] ∪ [ 20 ; + ∞ ) ∀ t ∈ ( - ∞ ; - 2 ] ∪ [ 2 ; + ∞ )  

⇒  Phương trình f (t) vô nghiệm  ⇔ m ∈ - 8 ; 20

⇒  Có 27 giá trị m nguyên thỏa mãn.

Không phải lớp 3 nhe nhầm lớp rùi

`2x^3 +6x^2 =x^2 +3x`

`<=> 2x^3 +6x^2 -x^2 -3x=0`

`<=> 2x^3 +5x^2 -3x=0`

`<=> x(2x^2 +5x-3)=0`

`<=> x(2x^2 +6x-x-3)=0`

`<=> x[2x(x+3)-(x+3)]=0`

`<=> x(2x-1)(x+3)=0`

\(< =>\left[{}\begin{matrix}x=0\\2x-1=0\\x+3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=0\\x=\dfrac{1}{2}\\x=-3\end{matrix}\right.\)

b)

`(2+x)^2 -(2x-5)^2=0`

`<=> (2+x-2x+5)(2+x+2x-5)=0`

`<=> (-x+7)(3x-3)=0`

\(< =>\left[{}\begin{matrix}-x+7=0\\3x-3=0\end{matrix}\right.\\ < =>\left[{}\begin{matrix}x=7\\x=1\end{matrix}\right.\)

`a) 2x^3 + 6x^2 = x^2 + 3x`

`=> 2x^3 + 6x^2 - x^2 - 3x = 0`

`=> 2x^3 + 5x^2 - 3x = 0`

`=> x(2x^2 + 5x - 3) = 0`

`=> x (2x^2 + 6x - x - 3) = 0`

`=> x [(2x^2 + 6x) - (x+3)] = 0`

`=> x [2x(x+3) - (x+3)] = 0`

`=> x (2x - 1)(x+3) = 0`

`=> x = 0` hoặc `2x - 1 = 0` hoặc `x + 3 = 0`

`=> x = 0` hoặc `x = 1/2` hoặc `x = -3`

`b) (2+x)^2 - (2x-5)^2 = 0`

`=> (2+x+2x-5)(2+x-2x+5) = 0`

`=> (3x - 3)(7-x) = 0`

`=> 3x - 3 = 0` hoặc `7 - x = 0`

`=> x = 1` hoặc `x = 7`

Biểu thức xác định khi x 2 - 36 ≠ 0 ,  x 2 + 6 x ≠ 0 , 6 – x ≠ 0 và 2x – 6  ≠  0

x 2 - 36 ≠ 0  ⇒ (x – 6)(x + 6)  ≠  0 ⇒ x  ≠  6 và x  ≠  -6

x 2 + 6 x ≠ 0  ⇒ x(x + 6)  ≠  0 ⇒ x  ≠  0 và x  ≠  -6

6 – x  ≠  0 ⇒ x  ≠  6

2x – 6  ≠  0 ⇒ x  ≠  3

Vậy x  ≠  0, x  ≠  3, x  ≠  6 và x  ≠  -6 thì biểu thức xác định.

Ta có:

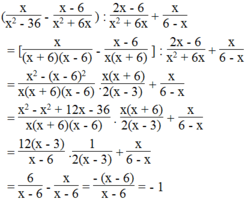
Vậy biểu thức không phụ thuộc vào biến x.