Chứng minh rằng nếu a2=bc(với a khác b và a khác c) thì a+b/a-b=c+a/c-a
AI TRẢ LỜI ĐÚNG MÌNH TICH
Chứng minh rằng nếu a^2 =bc với (a khác b và a khác c) thì a+b/a-b=c+a/c-a
\(a^2=bc\)
\(\Rightarrow\frac{a}{c}=\frac{b}{a}\)
Áp dụng tính chất của dãy tỉ số bằng nhau ta có :
\(\frac{a}{c}=\frac{b}{a}=\frac{a+b}{c+a}=\frac{a-b}{c-a}\)
\(\Rightarrow\frac{a+b}{a-b}=\frac{c+a}{c-a}\)
chứng minh rằng nếu a^2 = bc ( với a khác b và a khác c ) thì a+b / a-b = c+a / c-a
Do \(a^2=bc\Rightarrow\frac{a}{b}=\frac{c}{a}\)
Đặt \(\frac{a}{b}=\frac{c}{a}=k\Rightarrow\begin{cases}a=b.k\\c=a.k\end{cases}\)
Ta có:
\(\frac{a+b}{a-b}=\frac{b.k+b}{b.k-b}=\frac{b.\left(k+1\right)}{b.\left(k-1\right)}=\frac{k+1}{k-1}\left(1\right)\)
\(\frac{c+a}{c-a}=\frac{a.k+a}{a.k-a}=\frac{a.\left(k+1\right)}{a.\left(k-1\right)}=\frac{k+1}{k-1}\left(2\right)\)
Từ (1) và (2) \(\Rightarrow\frac{a+b}{a-b}=\frac{c+a}{c-a}\left(đpcm\right)\)
ta có :a^2=bc
⇒a.a=bc
⇒a/b=c/a
⇒a/c=b/a
Áp dụng tính chất dãy tỉ số bằng nhau a/c=b/a=a+b/c+a=a-b/c-a
⇒a+b/c+a=a-b/c-a
⇒a+b/a-b=c+a/c-a(điều phải chứng minh)
Giúp mình bài này với:
Cho (a^2 + b^2) / (c^2 + d^2) = (a x b) / (c x d) với a, b, c, d khác 0; c khác d và -d.
Chứng minh rằng hoặc a/b = c/d hoặc a/b = d/c.
Ai trả lời đúng mình sẽ k.
\(\frac{a^2+b^2}{c^2+d^2}=\frac{ab}{cd}\)
=> cd(a2 + b2) = ab(c2 + d2)
=> a2cd + b2cd = abc2 + abd2
=> a2cd + b2cd - abc2 - abd2 = 0
=> (a2cd - abc2) + (b2cd - abd2) = 0
=> ac(ad - bc) + bd(bc - ad) = 0
=> ac(ad - bc) - bd(ad - bc) = 0
=> (ac - bd)(ad - bc) = 0
=> \(\orbr{\begin{cases}ac-bd=0\\ad-bc=0\end{cases}}\Rightarrow\orbr{\begin{cases}ac=bd\\ad=bc\end{cases}}\Leftrightarrow\orbr{\begin{cases}\frac{a}{b}=\frac{d}{c}\\\frac{a}{b}=\frac{c}{d}\end{cases}}\Rightarrow\text{đpcm}\)
Chứng minh rằng:
Nếu a2 = bc (với a ≠ b và a ≠ c) thì a + b a - b = c + a c - a
Ta có:
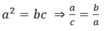
Theo tính chất dãy tỉ số bằng nhau ta có:
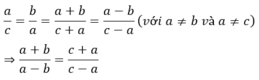
Chứng minh rằng nếu a2 = bc ( với a khác b và a khác c ) thì: \(\frac{a+b}{a-b}=\frac{c+a}{c-a}\)
vì a2=bc=\(\Rightarrow\frac{a}{b}\)=\(\frac{c}{a}\)
đặt \(\frac{a}{b}\)=\(\frac{c}{a}\)=k(k\(\ne\)0)\(\Rightarrow\)a=bk (1) ; c=ak(2) thay (1) vào \(\frac{a+b}{a-b}\)ta có \(\frac{bk+b}{bk-b}\)=\(\frac{b\left(k+1\right)}{b\left(k-1\right)}=\frac{k+1}{k-1}\)
thay (2) vào \(\frac{c+a}{c-a}\) ta có: \(\frac{ak+a}{ak-a}=\frac{a\left(k+1\right)}{a\left(k-1\right)}=\frac{k+1}{k-1}\)
do đó : \(\frac{a+b}{a-b}=\frac{c+a}{c-a}\)
Chứng minh rằng nếu\(a^2=bc\)(với a khác b và a khác c)thì\(\frac{a+b}{a-b}=\frac{c+d}{c-d}\).
Đề sai rồi nha bạn : .... thì \(\frac{a+b}{a-b}=\frac{c+a}{c-a}\) ( sửa lại )
Bài làm
Ta có \(a^2=bc=\frac{a}{c}=\frac{b}{a}\)
áp dụng dãy tỉ số bằng nhau ta có
\(\frac{a}{c}=\frac{b}{a}=\frac{a+b}{c+a}=\frac{a-b}{c-a}\Rightarrow\frac{a+b}{a-b}=\frac{c+a}{c-a}\left(đpcm\right)\)
hok tốt .
Ta có: a2 = bc
=> a.a = b.c
=> \(\frac{a}{c}=\frac{b}{a}\)=> \(\frac{a+b}{c+a}\)= \(\frac{a-b}{c-a}\)
Hình như bn ghi sai đề
Chứng minh rằng nếu a2=bc (a khác b và c)thì a+b/ a-b = c+a /c-a
chứng minh rằng nếu a^2=bc(với a khác b và a khác c) thi \(\frac{a+b}{a-b}=\frac{c+a}{c-a}\)
a2 = bc
=> a.a = b.c
=> \(\frac{a}{c}=\frac{b}{a}=\frac{a+b}{c+a}=\frac{a-b}{c-a}\)
=> \(\frac{a+b}{c+a}=\frac{a-b}{c-a}\)
=> \(\frac{a+b}{a-b}=\frac{c+a}{c-a}\)(Đpcm)
Chứng minh rằng nếu a mũ 2 = BC thì
Mũ 2 cộng c mũ 2 phần b mũ 2 + A2 = c b mở ngoặc b khác không đóng ngoặc