chứng tỏ phương trình \(ax^2+bx+c=0\) có nghiệm nếu a, b,c thỏa điều kiện: 5a-b+2c=0 và a≠0
TV
Những câu hỏi liên quan
chứng tỏ phương trình \(ax^2+bx+c=0\) có nghiệm nếu a, b,c thỏa điều kiện: 5a-b+2c=0 và a\(\ne\)0
cho phương trình ax^2+bx+c=0 với các số a,b,c là các số thực nghiệm khác 0 và thỏa mãn điều kiện a+b+2c=0. Chứng minh rằng phương trình trên luôn có nghiệm trên tập số thực
Đặt \(f\left(x\right)=ax^2+bx+c\).
\(f\left(0\right)=c;f\left(1\right)=a+b+c\)
Do \(a+b+2c=0\) nên c và \(a+b+c\) trái dấu. Suy ra f(0)f(1) < 0 nên f(x) = 0 luôn có ít nhất 1 nghiệm tren (0; 1).
Đúng 1
Bình luận (0)
cho hệ phương trình ax^2 +bx +c =0 với a khác 0 và 5a +2c=b chứng minh phương trình có nghiệm
Thay `b=5a+2c` vào `ax^2+bx+c=0`:
`ax^2+(5a+2c)x+c=0`
`=>Delta=(5a+2c)^2-4ac`
`=25a^2+20ac+4c^2-4ac`
`=25a^2+16ac+4c^2`
`=9a^2+(16a^2+16ac+4c^2)`
`=9a^2+(4a+2c)^2>=0`
`=>` ĐPCM
Đúng 0
Bình luận (0)
Cho phương trình: \(ax^2+bx+c=0\)
Chứng minh rằng nếu phương trình trên có nghiệm thì nó phải thỏa mãn một trong hai điều kiện sau:
1) \(a\left(a+2b+4c\right)< 0\)
2) \(5a+3b+2c=0\)
a) ax^2 + bx + c = 0
Để phương trình thỏa mãn điều kiện có 2 nghiệm dương phân biệt.
∆ > 0
=> b^2 - 4ac > 0
x1 + x2 = -b/a > 0
=> b và a trái dấu
x1.x2 = c/a > 0
=> c và a cùng dấu
Từ đó ta xét phương trình cx^2 + bx^2 + a = 0
∆ = b^2 - 4ac >0
x3 + x4 = -b/c, vì a và c cùng dấu mà b và a trái dấu nên b và c trái dấu , vì vậy -b/c >0
x3.x4 = a/c, vì a và c cùng dấu nên a/c > 0
=> phương trình cx^2 + cx + a có 2 nghiệm dương phân biệt x3 và x4
Vậy nếu phương trình ax^2 + bx + c = 0 có 2 nghiệm dương phân biệt thì phương trình cx^2 + bx + a = 0 cũng có 2 nghiệm dương phân biệt.
b) Ta có, vì x1, x2, x3, x4 không âm, dùng cô si.
x1 + x2 ≥ 2√( x1.x2 )
x3 + x4 ≥ 2√( x3x4 )
=> x1 + x2 + x3 + x4 ≥ 2[ √( x1.x2 ) + √( x3x4 ) ] (#)
Tiếp tục côsi cho 2 số không âm ta có
√( x1.x2 ) + √( x3x4 ) ≥ 2√[√( x1.x2 )( x3.x4 ) ] (##)
Theo a ta có
x1.x2 = c/a
x3.x4 = a/c
=> ( x1.x2 )( x3.x4 ) = 1
=> 2√[√( x1.x2 )( x3.x4 ) ] = 2
Từ (#) và (##) ta có
x1 + x2 + x3 + x4 ≥ 4
Đúng 0
Bình luận (0)
cho a,b.c là 3 só thực thỏa mãn 5a+3b+2c = 0.Chứng minh rằng phương trình ax^2 +bx+c = 0 luôn có nghiệm
cho 5a+2c=b. Chứng minh phương trình ax2 + bx+c=0 có nghiệm
\(\Delta\) = b2 - 4ac = (5a + 2c)2 - 4ac = 25a2 + 20ac + 4c2 - 4ac = 25a2 + 16ac + 4c2
= 9a2 + (16a2 + 16ac + 4c2)
= 9a2 + (4a + 2c)2 \(\ge\) 0 với mọi a; c
=> Pt đã cho luôn có nghiệm
Đúng 0
Bình luận (0)
Cho 3 số phân biệt a,b,c\(\in\)R . Chứng minh rằng phương trình:
\(ax^2+bx+c=0\) luôn có nghiệm nếu \(\dfrac{5}{4}a+\dfrac{3}{2}b+2c=0\)
Đặt \(f\left(x\right)=ax^2+bx+c\)
Hàm f(x) liên tục trên R
Ta có: \(f\left(1\right)=a+b+c\) ; \(f\left(\dfrac{1}{2}\right)=\dfrac{a}{4}+\dfrac{b}{2}+c\)
\(\Rightarrow f\left(1\right)+f\left(\dfrac{1}{2}\right)=\dfrac{5a}{4}+\dfrac{3b}{2}+2c=0\)
\(\Rightarrow f\left(1\right)=-f\left(\dfrac{1}{2}\right)\)
\(\Rightarrow f\left(1\right).f\left(\dfrac{1}{2}\right)=-\left[f\left(1\right)\right]^2\le0\)
\(\Rightarrow f\left(x\right)\) luôn có ít nhất 1 nghiệm thuộc \(\left[\dfrac{1}{2};1\right]\) hay pt đã cho luôn có nghiệm
Đúng 0
Bình luận (0)
Cho các số a, b, c thỏa mản điều kiện 0<a<b và phương trình ax2+ bx+ c=0 vô nghiệm.
Chứng minh \(\frac{a+b+c}{b-a}\)> 3
╔══╗
╚╗╔╝
╝(¯`v´¯)
╚══`.¸.Your lover’s name
╔♫═╗╔╗ ♥
╚╗╔╝║║♫═╦╦╦╔╗
╔╝╚╗♫╚╣║║║║╔╣
╚═♫╝╚═╩═╩♫╩═╝ ஜ۩۞۩ஜ YOU ஜ۩۞۩ஜ
▂ ▃ ▅ ▆ █ Type your status message █ ▆ ▅ ▃ ▂
★·.·´¯`·.·★ Type your status message ★·.·´¯`·.·★
..♩.¸¸♬´¯`♬.¸¸¤ Type your status message o ¤¸¸.♬´¯`♬¸¸.♩..
♬ •♩ ·.·´¯`·.·♭•♪ Type your status message e ♪ •♭·.·´¯`·.·♩ •♬
»——(¯` Type your status message ´¯)——» ¸
.·’★¸.·’★*·~-.¸-(★ Type your status message ★)-,.-~*¸.·’★¸.·’★
(♥).•*´¨`*•♥•(★) Type your status message (★)•♥•*´¨`*•.(♥)
• ♥ⓛⓞⓥⓔ♥☜ facebook emoons ☞♥ⓛⓞⓥⓔ♥
◢♂◣◥♀◤ facebook emoons ◢♂◣◥♀◤ ¸
.•♥•.¸¸.•♥• Type your status message •♥•.¸¸.•♥•.¸
☜♥☞ º°”˜`”°º☜(Type your status message )☞ º°”˜`”°☜♥☞
k mk nha
Đúng 0
Bình luận (0)
toán lớp mấy đấy???
Ta có : (4a – b)^2 ≥ 0 ⇔16a^2 – 8ab + b^2 ≥ 0 (1)
Mà phương trình : ax^2 + bx + c = 0 vô nghiệm nên: ∆ = b^2 – 4ac < 0 ⇔ 4ac > b^2 (2)
Từ (1) và (2) => 16a^2 – 8ab + 4ac > 16a^2 – 8ab + b^2> 0
=> 16a^2 – 8ab + 4ac > 0 => 4a(4a – 2b + c) > 0
=> 4a – 2b + c > 0 do (a > 0 => 4a > 0)
=> a + b + c + 3a – 3b > 0 => a + b + c > 3(b – a) => 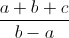 > 3
> 3
Xem thêm câu trả lời
Cho phương trình ax^2 + bx + c = 0 có 2 nghiệm x1 = -1 và x2 =2 . Tìm bộ số a,b,c thỏa mãn điều kiện trên và cho bik có tất cả bao nhiêu bộ số



