vẽ O là giao điểm của đường thẳng xy và đường thẳng a
HY
Những câu hỏi liên quan
Cho tam giác ABC . Qua A vẽ đường thẳng xy//BC . Trên cạnh BC lấy điểm D vẽ DE//AB, DF//AC(E,F thuộc xy).Gọi M là giao điểm của AB và DF. Gọi N là giao của AC và DE. Gọi O là giao của AD và CF. Chứng minh rằng:
a) 3 điểm B , O, E thẳng hàng b) 3 điểm M, O , N thẳng hàng
H24
2 tháng 10 2021 lúc 9:36
4. Cho ∆ABC (AB < BC). Qua A vẽ đường thẳng xy//BC. Từ điểm M trên cạnh BC vẽ các đường thẳng song song với AB, AC chúng cắt xy theo thứ tự tại D và E.
1) C/m: AD = BM và ∆ABC=∆MDE
2) Gọi O là giao điểm của AM và CE. Chứng minh 3 điểm B, O, D thẳng hàng
3) Tìm vị trí của điểm M trên cạnh BC để AM vuông góc với CE
\(1,BM//AD\Rightarrow\widehat{BMA}=\widehat{MAD};\widehat{BAM}=\widehat{AMD}\\ \left\{{}\begin{matrix}\widehat{BMA}=\widehat{MAD}\\AM.chung\\\widehat{BAM}=\widehat{AMD}\end{matrix}\right.\Rightarrow\Delta ABM=\Delta MDA\left(g.c.g\right)\\ \Rightarrow AD=BM;MD=AB\\ \)
Chứng minh tương tự, ta được \(\Delta ACM=\Delta MEA\left(g.c.g\right)\)
\(\Rightarrow AE=MC;ME=AC\\ \Rightarrow DE=DA+AE=BM+MC=BC\\ \left\{{}\begin{matrix}DE=BC\\AC=ME\\AB=MD\end{matrix}\right.\Rightarrow\Delta ABC=\Delta MDE\left(c.c.c\right)\)
\(b,\)
\(AE//CM\Rightarrow\widehat{OAE}=\widehat{OMC};\widehat{OEA}=\widehat{OCM}\\ Mà.AE=CM\\ \Rightarrow\Delta OAE=\Delta OMC\left(g.c.g\right)\\ \Rightarrow OA=OM\\ AD//BM\Rightarrow\widehat{OAD}=\widehat{OMB}\\ Mà.AD=BM\\ \Rightarrow\Delta OAD=\Delta OMB\left(c.g.c\right)\\ \Rightarrow\widehat{AOD}=\widehat{MOB}\\ \Rightarrow\widehat{BOD}=\widehat{AOD}+\widehat{AOB}=\widehat{MOB}+\widehat{AOB}=\widehat{AOM}=180^0\\ \Rightarrow B;O;D.thẳng.hàng\)
Đúng 1
Bình luận (4)
Cho đường thẳng xy và đường tròn (O) không giao nhau vẽ OH vuông góc với xy (H € xy ). Từ điểm A trên đường thẳng xy vẽ tiếp tuyến AB với đường tròn (B tiếp điểm). Vẽ các tuyến AMN sao cho AB và MN nằm trên hai nửa mặt phẳng bờ AO. Gọi D là trung điểm của MN. a) Chứng minh tứ giác ABOD nội tiếp b) Chứng minh AB²= AM.AN
a: ΔOMN cân tại O có OD là trung tuyến
nên OD vuông góc NA
góc ODA=góc OBA=90 độ
=>ODBA nội tiếp
b; Xét ΔABM và ΔANB có
góc ABM=góc ANB
góc BAM chung
=>ΔABM đồng dạng với ΔANB
=>AB/AN=AM/AB
=>AB^2=AN*AM
Đúng 0
Bình luận (0)
Cho tam giác ABC. Qua A vẽ đường thẳng xy song song BC. Trên cạnh BC lấy một điểm D. Vẽ DE song song AB, DF song song AC (E,F thuộc xy). Gọi M là giao điểm của AB và DF. Gọi N là giao điểm của AC và DE. Gọi O là giao điểm của AD và CF. Chứng minh rằng:
a) Ba điểm B,O,E thẳng hàng.
b) Ba điểm M,O,N thẳng hàng.
Vẽ hình theo yêu cầu sau :a, Hai đường thẳng xy và uv cắt nhau tại O. Trên xy lấy A, B sao cho O là trung điểm của AB. Trên uv lấy C,D sao cho O là trung điểm của CD. Lấy I là trung điểmcủa AC. Nối IO kéo dài cắt BD ở Hb, Hai tia đối nhau Ox, Oy. Trên Oy lấy A, B sao cho A nằm giữa O và B. Vẽ đường thẳng a đi qua O, đường thẳng b đi qua B. Gọi C là giao điểm của a và b, vẽ đoạn thẳng AC
Đọc tiếp
Vẽ hình theo yêu cầu sau :
a, Hai đường thẳng xy và uv cắt nhau tại O. Trên xy lấy A, B sao cho O là trung điểm của AB. Trên uv lấy C,D sao cho O là trung điểm của CD. Lấy I là trung điểmcủa AC. Nối IO kéo dài cắt BD ở H
b, Hai tia đối nhau Ox, Oy. Trên Oy lấy A, B sao cho A nằm giữa O và B. Vẽ đường thẳng a đi qua O, đường thẳng b đi qua B. Gọi C là giao điểm của a và b, vẽ đoạn thẳng AC
Qua điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC của đường tròn (B và C là các tiếp điểm).Gọi E là trung điểm của đoạn thẳng AC,F là giao điểm thú hai của đường thẳng EB với đường tròn (O),K là giao điểm thứ hai của đường thẳng AF với đường tròn (O).Chứng minh:a.Tứ giác ABOC là tứ giác nội tiếp và tam giác ABF đồng dạng với tam giác AKBb.BF . CK CF . BK
Đọc tiếp
Qua điểm A nằm ngoài đường tròn (O) vẽ hai tiếp tuyến AB và AC của đường tròn (B và C là các tiếp điểm).Gọi E là trung điểm của đoạn thẳng AC,F là giao điểm thú hai của đường thẳng EB với đường tròn (O),K là giao điểm thứ hai của đường thẳng AF với đường tròn (O).Chứng minh:
a.Tứ giác ABOC là tứ giác nội tiếp và tam giác ABF đồng dạng với tam giác AKB
b.BF . CK = CF . BK
a: Xét tứ giác ABOC có
\(\widehat{ABO}+\widehat{ACO}=180^0\)
Do đó: ABOC là tứ giác nội tiếp
Đúng 1
Bình luận (0)
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A; 13cm) :
a) Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy
b) Gọi hai giao điểm nói trên là B và C. Tính độ dài BC ?
1. Cho đường tròn ( O) và đường thẳng xy nằm ngoài đường tròn. Từ O kẻ OA vuông góc với xy. Qua A vẽ cát tuyến cắt đường tròn (O) ở B và C. Tiếp tuyến với đường tròn (O) tại B và C cắt xy ở D và E. Chứng minh: A là trung điểm của DE2. Cho tứ giác ABCD có AB BD nội tiếp đường tròn (O) . Từ A vẽ tiếp tuyến với đường tròn (O) cắt đường thẳng BC ở Q , gọi R là giao điểm của AB và CD. Chứng minh: a) tứ giác AQRC nội tiếp được 1 đường tròn b) QR//AD
Đọc tiếp
1. Cho đường tròn ( O) và đường thẳng xy nằm ngoài đường tròn. Từ O kẻ OA vuông góc với xy. Qua A vẽ cát tuyến cắt đường tròn (O) ở B và C. Tiếp tuyến với đường tròn (O) tại B và C cắt xy ở D và E. Chứng minh: A là trung điểm của DE
2. Cho tứ giác ABCD có AB = BD nội tiếp đường tròn (O) . Từ A vẽ tiếp tuyến với đường tròn (O) cắt đường thẳng BC ở Q , gọi R là giao điểm của AB và CD. Chứng minh:
a) tứ giác AQRC nội tiếp được 1 đường tròn
b) QR//AD
Ta có: tỨ giác OCEA nội tiếp
=> \(\widehat{OCA}=\widehat{OEA}\)(1)
Vì OC=OB
=> Tam giác OBC cân
=> \(\widehat{OCA}=\widehat{OCB}=\widehat{OBC}\)(2)
Tứ giác ODAB nội tiếp
=> \(\widehat{ODA}=\widehat{OBC}\)( cùng bù với góc OBA) (3)
Từ (1), (2), (3)
=> \(\widehat{ODA}=\widehat{OEA}\)
=> Tam giác ODE cân có OA là đươngcao
=> OA là đường trung tuyến
=> A là trung điểm của DE
Đúng 0
Bình luận (0)
Cho điểm A cách đường thẳng xy là 12cm. Vẽ đường tròn (A ; 13cm). Chứng minh rằng đường tròn (A) có hai giao điểm với đường thẳng xy
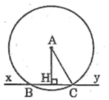
Kẻ AH ⊥ xy
Ta có: AH = 12cm
Bán kính đường tròn tâm I là 13cm nên R = 13cm
Mà AH = d = 12cm
Nên suy ra d < R
Vậy (A; 13cm) cắt đường thẳng xy tại hai điểm phân biệt B và C
Đúng 0
Bình luận (0)