cho ▲ABC, điểm M là trung điểm BC. Chứng minh rằng:
\(\dfrac{AB+AC-BC}{2}\)<AM<\(\dfrac{AB+AC}{2}\)
Tuyển Cộng tác viên Hoc24 nhiệm kì 26 tại đây: https://forms.gle/dK3zGK3LHFrgvTkJ6
Cho tam giác ABC, gọi M là trung điểm của BC. Chứng minh rằng \(\dfrac{AB+AC-BC}{2}\) < AM < \(\dfrac{AB+AC}{2}\)
Cho tam giác ABC có BC=2.AB,M là trung điểm của BC,D là trung điểm của BM. Chứng minh rằng AC=2.AD
Cho tam giác ABC có BC=2.AB,M là trung điểm của BC,D là trung điểm của BM. Chứng minh rằng AC=2.AD
Cho tam giác ABC. Gọi M là trung điểm của BC
a) Chứng minh AM < \(\dfrac{AB+AC}{2}\)
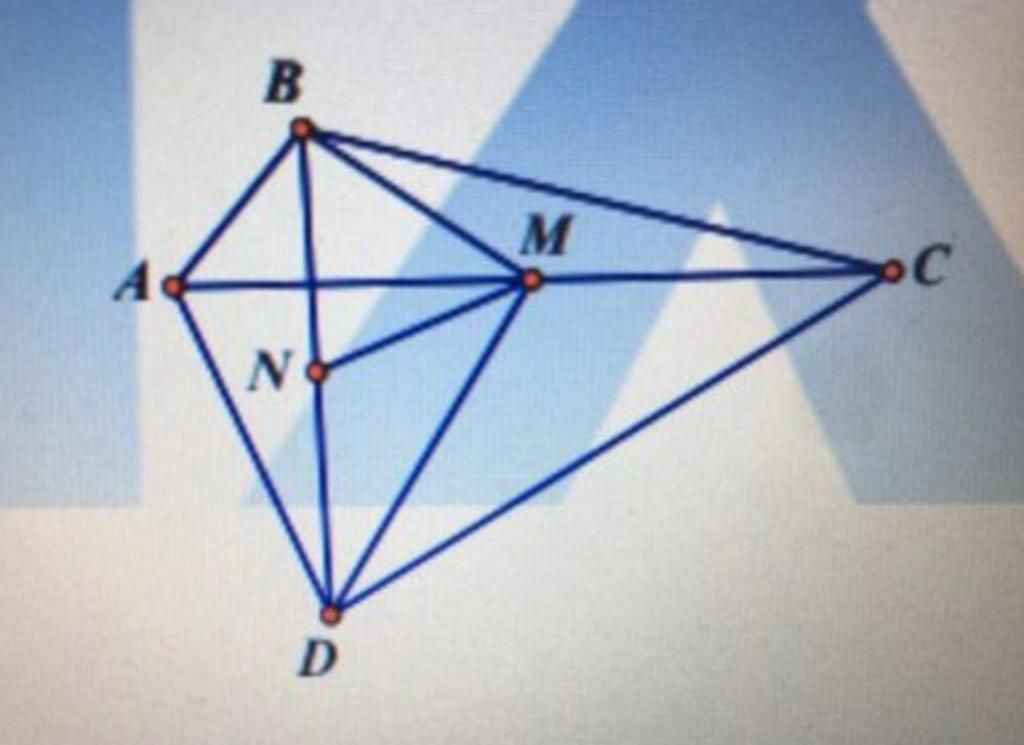
b) Cho bốn điểm A, B, C, D như hình vẽ. gọi thứ tự là trung điểm của AC và BD. Chứng minh AB+BC+CD+DA > 4.MN
a:
Lấy D sao cho M là trung điểm của AD
Xét tứ giác ABDC có
M là trung điểm chung của AD và BC
=>ABDC là hình bình hành
(AB+AC)=AB+BD>AD
=>AB+AC>2AM
=>(AB+AC)/2>AM
cho tam giác nhọn ABC (AB<AC). gọi lần lượt là trung điểm của AB,AC và BC. Kẻ AH vuông gốc với BC tại H, AH cắt DE tại M.
1) chứng minh rằng : DM/BH.
2) chứng minh rằng : M là trung điểm AH và tam giác AEH cân
3) trên tia đối của tia DH lấy điểm K sao cho DH=DK. chứng minh rằng, tứ giá DEFH lầ hình thang cân và tứ giác KACB là hình vuông.
4) giả sử AB=AF. chứng minh rằng : ba điểm K,M,F thẳng hàng
1: Xét ΔABC có
D là trung điểm của AB
E là trung điểm của AC
Do đó: DE là đường trung bình của ΔBAC
Suy ra: DE//BC
hay DM//BH
2: Xét ΔABH có
D là trung điểm của AB
DM//BH
Do đó: M là trung điểm của AH
Bài 1: Cho tam giác ABC vuông tại A, AB > AC. M là trung điểm của BC.
Trên tia đối của tia MA lấy điểm D sao cho MD = MA.
a) Chứng minh rằng: AB = DC và AB // DC.
b) Chứng minh rằng:
Tam giác ABC=tam giác CDA
từ đó suy ra Am=BC trên 2
c) Trên tia đối của tia AC lấy điểm E sao cho AE=AC. Chứng minh rằng:
BE// AM.
d) Tìm điều kiện của tam giác ABC để AC bằng BC trên 2
e) Gọi O là trung điểm của AB. Chứng minh rằng: Ba điểm E, O, D thẳng
hàng.
a) Xét tam giác CMA và tam giác BMD có :
\(\hept{\begin{cases}MC=MB\\AM=MD\\\widehat{AMC}=\widehat{BMD}\end{cases}\Rightarrow\Delta CMA=\Delta BMD}\)
=> \(\hept{\begin{cases}AC=BD\\\widehat{BDM}=\widehat{ACM}\end{cases}\Rightarrow BD//AC}\)
=> ACBD là hình bình hành
=> \(\hept{\begin{cases}AB=CD\\AB//CD\end{cases}}\)=> đpcm
b) Xét tam giác ABC và tam giác CDA có :
\(\hept{\begin{cases}AB=CD\\\widehat{CAB}=\widehat{ACD}=90^∗\end{cases}\Rightarrow\Delta ABC=\Delta CDA}\)( Lưu ý : Vì không có dấu kí hiệu " độ " nên em dùng tạm dấu *)
Chung AC
=> AD=BC
=> \(AM=\frac{1}{2}.AD=\frac{1}{2}.BC\)=> đpcm
c) Xét tam giác ABC có :
M là trung điểm BC
A là trung điểm CE
Từ 2 điều trên =>AM là đường trung bình => AM//BE ( đpcm )
e) AM //BE => AD // BE
Tam giác CBE có BA vừa là đường cac ,vừa là trung tuyến => tam giác CBE cân ở B
=> \(\hept{\begin{cases}BC=BE\\AD=BC\end{cases}\Rightarrow AD=EB}\)
Mà AD//BE => ABDE là hình bình hành => AB cắt DE ở trung điểm
=> E,O , D thẳng hàng => đpcm
cho tam giác abc =8cm ac=12cm lấy điểm m trên cạnh ab sao cho bm=2cm lấy điểm n trên cạnh ac sao cho bn,ac,cn =3cm a, chứng minh rằng mn//bc b,gọi k là trung điểm của bc, tia ak cắt mn tại i, chứng minh rằng ni/kc=ai/ak c, chứng minh rằng i là trung điểm của mn
a: AM=6-2=6cm
AN=12-3=9cm
=>AM/AB=AN/AC
=>MN//BC
b: Xet ΔAKC có NI//KC
nên NI/KC=AI/AK
Xét ΔABK có MI//BK
nên MI/BK=AI/AK
=>NI/KC=MI/BK
c: NI/KC=MI/BK
KC=KB
=>NI=MI
=>I là tđ của MN
Cho tam giác ABC có AB=3 cm ; AC= 4,5 cm. Lấy điểm M trên cạnh AB sao cho AM = 1 cm , lấy điểm N trên cạnh AC sao cho AN = 1,5 cm.
a) Chứng minh rằng MN // BC.
b) Gọi I là trung điểm của MN , tia AI cắt BC tại K.
+) CM \(\dfrac{MI}{BK}\)= \(\dfrac{AI}{AK}\)
+) CM K là trung điểm của BC .
c) CM IK , MK và BN đồng quy tại một điểm .
tự vẽ hình
a, có AM/AB=1/3
mà AN/AC=1,5/4,5=1/3
=> AM/AB=AN/AC
=> MN//BC
b, Ta có MN//BC=> tam giác AMN đồng dạng tam giác ABC
=> <AMN= <ABC
Xét tam giác AMI và tam giác ABK
<AMI= <ABC (cmt)
<MAK chung
=> tam giác AMI đồng dạng tam giác ABK
MI/BK= AI/AK
cho tam giác nhọn ABC (AB < AC) ; gọi M là trung điểm là trung điểm của BC. Trên tia đối của tia MA xác định điểm E sao cho ME = MA.
1. Chứng minh tam giác MAC = tam giác MEB
2. Chứng minh AC = EB
Kẽ EH vuông góc với BC, (H thuộc BC). Chứng minh rằng EH < MA.
1: Xét ΔMAC và ΔMEB có
MA=ME
\(\widehat{AMC}=\widehat{EMB}\)
MC=MB
Do đó: ΔMAC=ΔMEB
2: Ta có: ΔMAC=ΔMEB
nên AC=EB