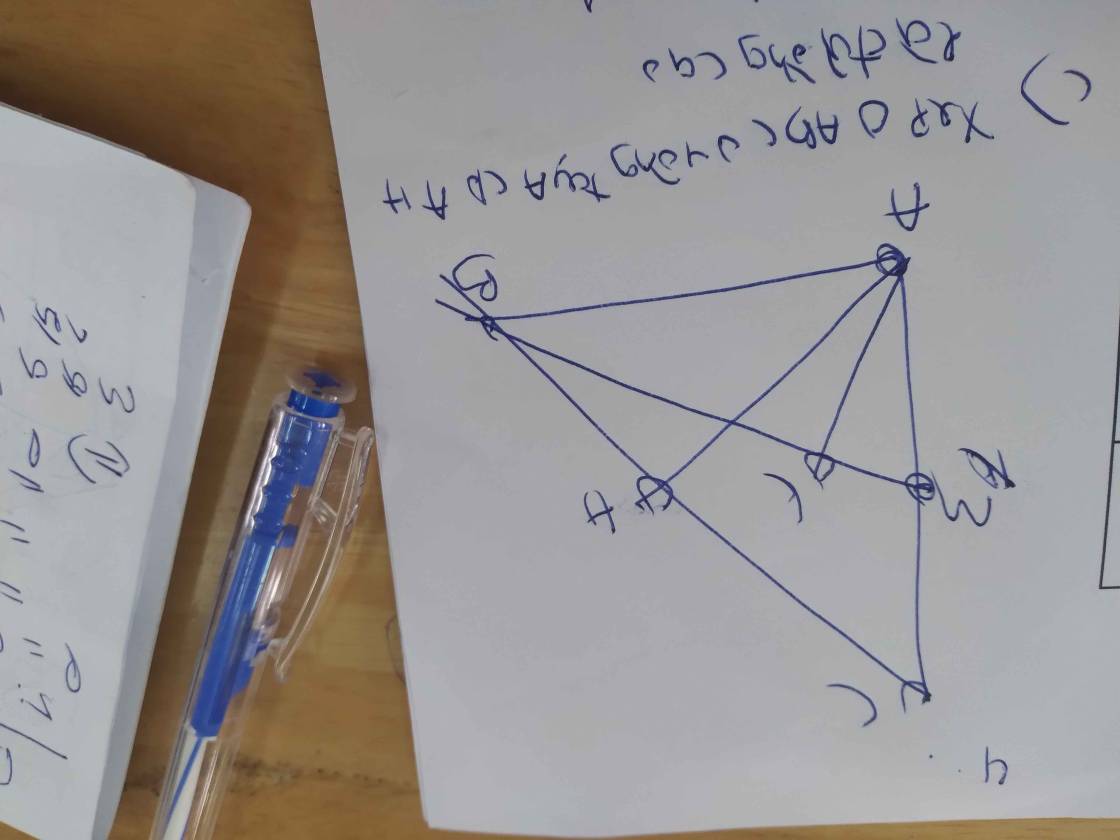
Giúp em bài 633 từ câu 5 với ạ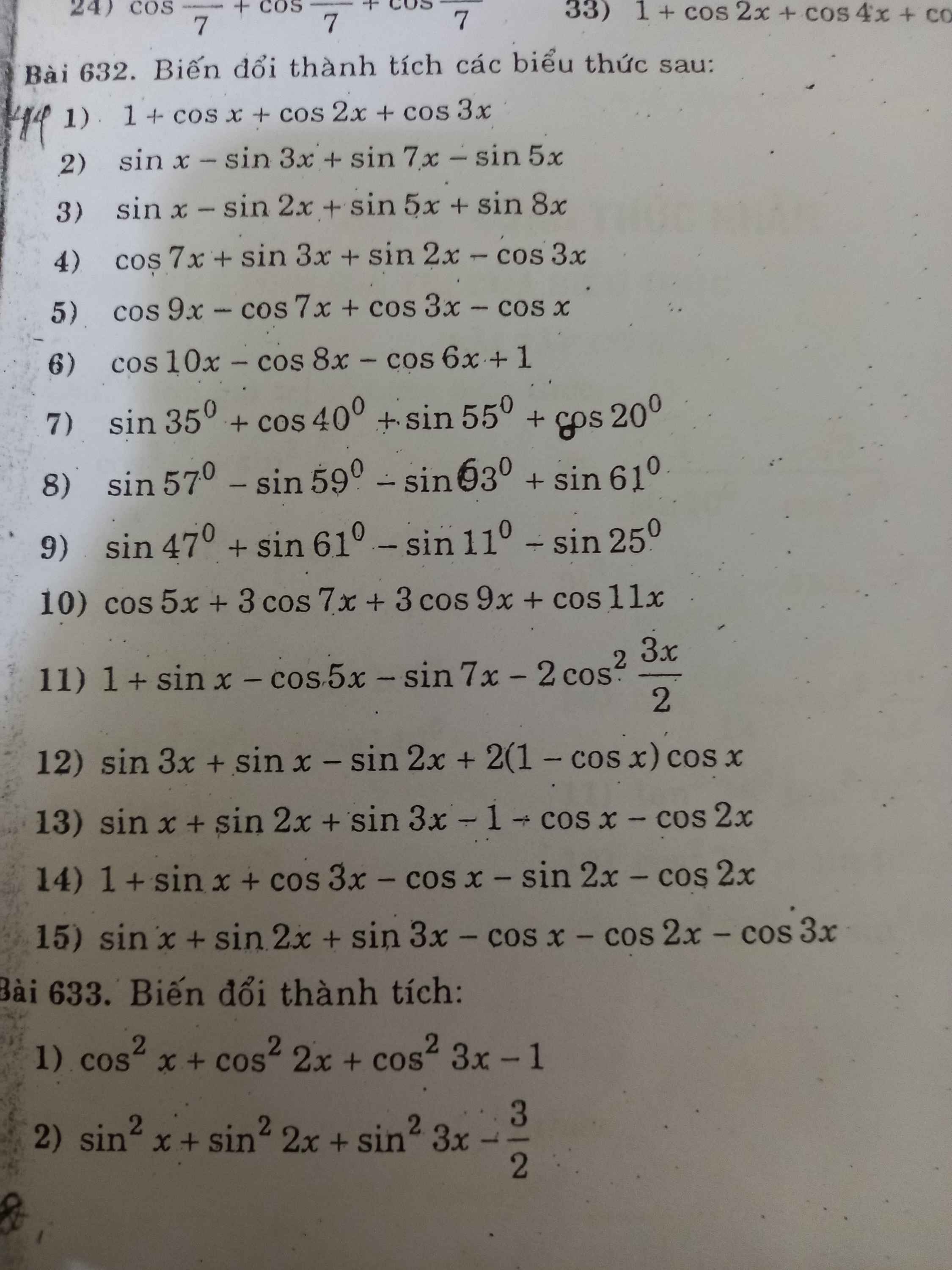
TD
Những câu hỏi liên quan
Rất mong các anh chị giúp bài này, em cần gấp lắm ạ!!!!!!!!!( em hông có sách TA ạ)
- ghi các cụm từ đi với từ Go (lớp 5)
- dùng mẫu câu và cụm từ đã học để đặt 10 câu hỏi và câu trả lời( lớp 5)
Em cần gấp lắm ạ!!!!!!!!!
go after somebody. đuổi theo, đi theo sau ai đó ...go along with somebody. đi cùng ai đó đến nơi nào đó ...go away. đi nơi khác, đi khỏi, rời (nơi nào). ...go back on one's word. không giữ lời. ...go beyond something. vượt quá, vượt ngoài (cái gì) ...go by. đi qua, trôi qua (thời gian) ...go down. giảm, hạ (giá cả) ...go down with. mắc bệnh.đây là một số cụm động từ đi với go
mng giúp em với ạ, em đg cần gấp ạ, bài điền từ từ câu 1 đến 10 ạ em kamon!

1. illegal
2. traffic jam
3. seatbelt
4. safely
5. railway station
6. safety
7. traffic signs
8. helicopter
9. tricycle
10. boat
Đúng 1
Bình luận (0)
Em rút được bài học gì cho bản thên qua đoạn văn trên ( viết từ 3-5 câu )
Giúp với ạ 
M.n giúp em với ạ . Đề bài đây ạ , em chỉ tick ch người trả lời đúng thôi ạ ( Em cảm mon m.n trước ạ , mai em nộp bài rrofi còn ai thức giúp em với ạ ! )Đề bài : Từ câu nói của người cha trong văn bản Mẹ tôi của nhà văn . Ét - môn - đô đơ A - mi - xi : Con hãy nhớ rằng , tình yêu thương , kính trọng cha mẹ là tình cảm thiêng liêng hơn cả . Thật xấu hổ và nhục nhã cho kẻ nào chà đạp lên tình yêu thương đó . Hãy viết một bài văn ngắn trình bày suy nghĩ của em về câu nói đó . M.n còn thức giúp...
Đọc tiếp
M.n giúp em với ạ . Đề bài đây ạ , em chỉ tick ch người trả lời đúng thôi ạ ( Em cảm mon m.n trước ạ , mai em nộp bài rrofi còn ai thức giúp em với ạ ! )
Đề bài : Từ câu nói của người cha trong văn bản " Mẹ tôi " của nhà văn . Ét - môn - đô đơ A - mi - xi : " Con hãy nhớ rằng , tình yêu thương , kính trọng cha mẹ là tình cảm thiêng liêng hơn cả . Thật xấu hổ và nhục nhã cho kẻ nào chà đạp lên tình yêu thương đó " . Hãy viết một bài văn ngắn trình bày suy nghĩ của em về câu nói đó . M.n còn thức giúp em với ạ , 6h sáng mai em phải học rồi ạ ( Em cầu xin m.n đó )
Ai còn thức giúp em với ạ , em sẽ vào trang cá nhân của 2 người đầu tiên và tick 5 lần cho câu trả lời của người đó ạ , người thứ 3 em sẽ tick 2 lần ạ . M.n giúp em với , gấp lắm ạ !![]()
Đúng 0
Bình luận (0)
Đến sáng ngày mai ai giúp em thì ko kịp nộp bài nữa nên 12h tối nay và sáng mai em ko tick ạ . Mong m.n thoong cảm và giúp cho em với ạ
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Giúp em từ câu 4 đến 13 bài 614 với ạ
13:
\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}sin\left(\dfrac{pi}{33}\right)\cdot cos\left(\dfrac{pi}{33}\right)\cdot cos\left(\dfrac{2pi}{33}\right)\cdot cos\left(\dfrac{4pi}{33}\right)\cdot cos\left(\dfrac{8pi}{33}\right)\cdot cos\left(\dfrac{16pi}{33}\right)\)
\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}\cdot\dfrac{1}{2}\cdot sin\dfrac{2}{33}pi\cdot cos\left(\dfrac{2}{33}pi\right)cos\left(\dfrac{4}{33}pi\right)\cdot cos\left(\dfrac{8}{33}pi\right)\cdot cos\left(\dfrac{16}{33}pi\right)\)
\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}\cdot\dfrac{1}{2}\cdot sin\dfrac{2}{33}pi\cdot cos\left(\dfrac{2}{33}pi\right)cos\left(\dfrac{4}{33}pi\right)\cdot cos\left(\dfrac{8}{33}pi\right)\cdot cos\left(\dfrac{16}{33}pi\right)\)\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}\cdot\dfrac{1}{4}\cdot sin\dfrac{4}{33}pi\cdot cos\left(\dfrac{4}{33}pi\right)\cdot cos\left(\dfrac{8}{33}pi\right)\cdot cos\left(\dfrac{16}{33}pi\right)\)
\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}\cdot\dfrac{1}{8}\cdot sin\dfrac{8}{33}pi\cdot cos\left(\dfrac{8}{33}pi\right)\cdot cos\left(\dfrac{16}{33}pi\right)\)
\(=\dfrac{1}{sin\left(\dfrac{pi}{33}\right)}\cdot\dfrac{1}{16}\cdot sin\dfrac{16}{33}pi\cdot cos\left(\dfrac{16}{33}pi\right)\)
\(=\dfrac{1}{sin\left(\dfrac{pi}{3}\right)}\cdot\dfrac{1}{32}\cdot sin\dfrac{32}{33}pi\)
=1/32
10:
\(=\dfrac{1}{2}\left[cos100+cos60\right]+\dfrac{1}{2}\cdot\left[cos100+cos20\right]\)
=cos100+1/2*cos20+1/4
6:
sin6*cos12*cos24*cos48
=1/cos6*cos6*sin6*cos12*cos24*cos48
=1/cos6*1/2*sin12*cos12*cos24*cos48
=1/cos6*1/4*sin24*cos24*cos48
=1/cos6*1/8*sin48*cos48
=1/cos6*1/16*sin96
=1/16
Đúng 0
Bình luận (0)
giúp em câu 5 với bài dưới với ạ😭
Giúp em với ạ từ bài 1-5 ạ
Bài 3 :
\(\Leftrightarrow\sqrt{9x^2-6x+1}=\sqrt{\left(3x-1\right)^2}=\left|3x-1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}3x-1=5\\3x-1=-5\end{matrix}\right.\)
\(\Leftrightarrow\left[{}\begin{matrix}x=2\\x=-\dfrac{4}{3}\end{matrix}\right.\)
Vậy ...
Bài 5 :
Ta có :\(x-5\sqrt{x}+7=x-2.\sqrt{x}.\dfrac{5}{2}+\dfrac{25}{4}+\dfrac{3}{4}=\left(\sqrt{x}-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\)
Thấy : \(\left(\sqrt{x}-\dfrac{5}{2}\right)^2\ge0\)
\(\Rightarrow\left(\sqrt{x}-\dfrac{5}{2}\right)^2+\dfrac{3}{4}\ge\dfrac{3}{4}\)
\(\Rightarrow P=\dfrac{1}{x-5\sqrt{x}+7}=\dfrac{1}{\left(\sqrt{x}-\dfrac{5}{2}\right)^2+\dfrac{3}{4}}\le\dfrac{1}{\dfrac{3}{4}}=\dfrac{4}{3}\)
Vậy \(Max_P=\dfrac{4}{3}\Leftrightarrow\sqrt{x}-\dfrac{5}{2}=0\Leftrightarrow x=\dfrac{25}{4}\)
Đúng 0
Bình luận (0)
Bài 1:
a) Ta có: \(\sqrt{25}\cdot\sqrt{144}+\sqrt[3]{-27}-\sqrt[3]{216}\)
\(=5\cdot12-3-6\)
\(=60-9=51\)
b) Ta có: \(\sqrt{8.1\cdot360}\)
\(=\sqrt{8.1\cdot10\cdot36}\)
\(=\sqrt{81\cdot36}\)
\(=9\cdot6=54\)
Bài 2:
a) Ta có: \(\sqrt{80}-\sqrt{\left(2-\sqrt{5}\right)^2}+\sqrt{3\dfrac{1}{5}}\)
\(=4\sqrt{5}-\sqrt{5}+2+\dfrac{4}{\sqrt{5}}\)
\(=3\sqrt{5}+2+\dfrac{4\sqrt{5}}{5}\)
\(=\dfrac{10+19\sqrt{5}}{5}\)
b) Ta có: \(\dfrac{\sqrt{6}-\sqrt{3}}{1-\sqrt{2}}+\dfrac{3+6\sqrt{3}}{\sqrt{3}}-\dfrac{13}{\sqrt{3}+4}\)
\(=\dfrac{-\sqrt{3}\left(1-\sqrt{2}\right)}{1-\sqrt{2}}+\dfrac{\sqrt{3}\left(\sqrt{3}+6\right)}{\sqrt{3}}-\dfrac{13\left(4-\sqrt{3}\right)}{\left(4+\sqrt{3}\right)\left(4-\sqrt{3}\right)}\)
\(=-\sqrt{3}+\sqrt{3}+6-4+\sqrt{3}\)
\(=2+\sqrt{3}\)
Đúng 0
Bình luận (0)
Bài 3:
Ta có: \(\sqrt{9x^2+6x+1}=5\)
\(\Leftrightarrow\sqrt{\left(3x+1\right)^2}=5\)
\(\Leftrightarrow\left|3x+1\right|=5\)
\(\Leftrightarrow\left[{}\begin{matrix}3x+1=5\\3x+1=-5\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}3x=4\\3x=-6\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{4}{3}\\x=-2\end{matrix}\right.\)
Vậy: \(S=\left\{\dfrac{4}{3};-2\right\}\)
Bài 4:
a) ĐKXĐ: \(\left\{{}\begin{matrix}x\ge0\\x\ne1\end{matrix}\right.\)
b) Ta có: \(A=\left(\dfrac{\sqrt{x}+1}{\sqrt{x}-1}-\dfrac{\sqrt{x}-1}{\sqrt{x}+1}-\dfrac{8\sqrt{x}}{x-1}\right):\dfrac{4\sqrt{x}-8}{1-x}\)
\(=\left(\dfrac{\left(\sqrt{x}+1\right)^2-\left(\sqrt{x}-1\right)^2-8\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\right):\dfrac{4\sqrt{x}-8}{-\left(x-1\right)}\)
\(=\dfrac{x+2\sqrt{x}+1-x+2\sqrt{x}-1-8\sqrt{x}}{\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}\cdot\dfrac{-\left(\sqrt{x}-1\right)\left(\sqrt{x}+1\right)}{4\left(\sqrt{x}-2\right)}\)
\(=\dfrac{4\sqrt{x}}{4\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}}{\sqrt{x}-2}\)
Đúng 0
Bình luận (0)
Anh chị ơi giúp em bài kiểm tra lớp 9 với ạ .em còn câu 5 6 7 anh chị giúp em với .Em cảm ơn rất nhiều ạ!!!!!!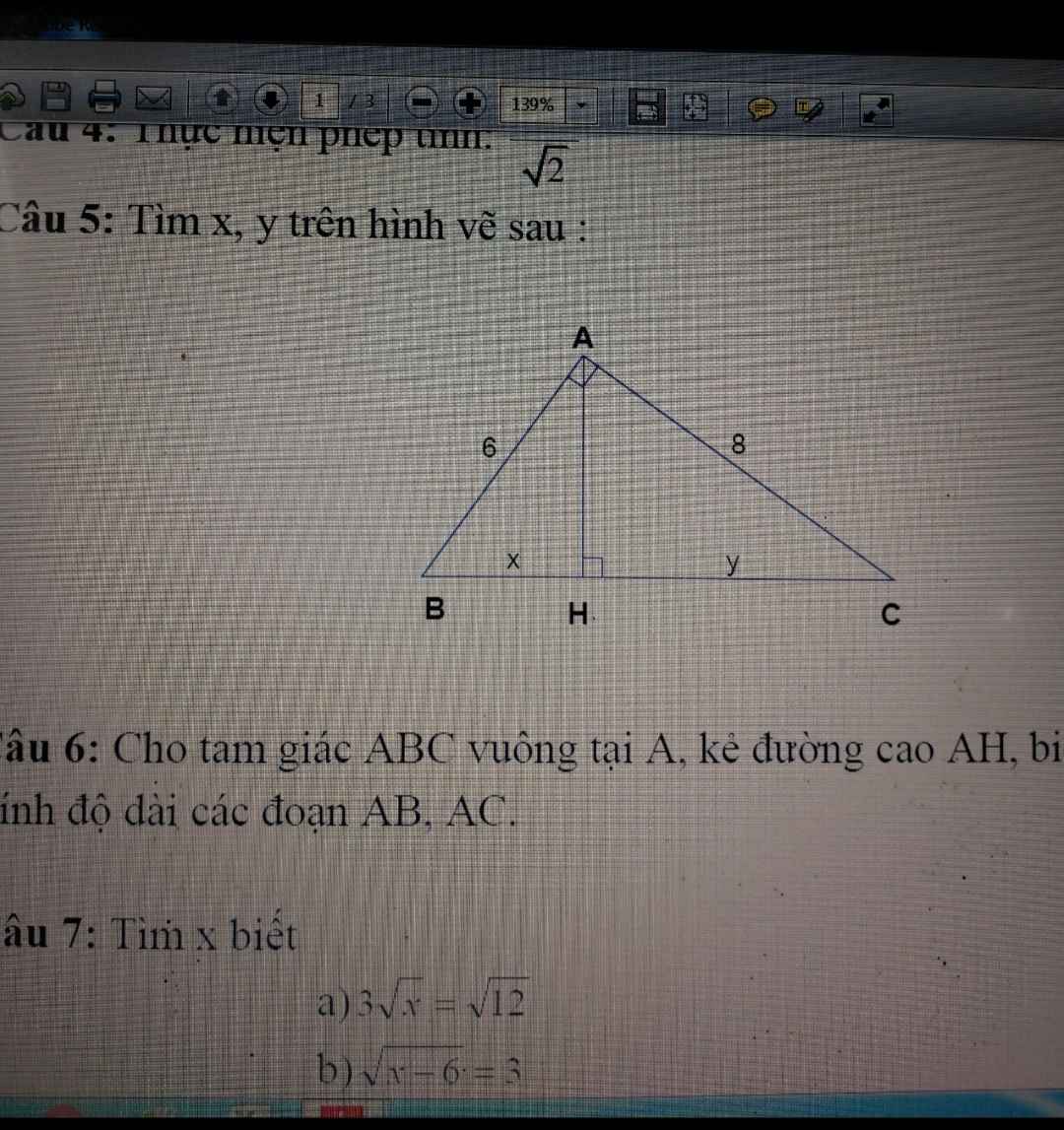
câu 5:
x=3,6
y=6,4
câu 6: chụp lại đề
câu 7:
a)ĐKXĐ: \(x\ge0\)
\(3\sqrt{x}=\sqrt{12}\\ \Rightarrow9x=12\\ \Rightarrow x=\dfrac{4}{3}\)
b) ĐKXĐ: \(x\ge6\)
\(\sqrt{x-6}=3\\ \Rightarrow x-6=9\\ \Rightarrow x=15\)
Đúng 0
Bình luận (0)
Câu 5:
Áp dụng định lý Pi-ta-go ta có:
\(AB^2+AC^2=BC^2\\ \Rightarrow BC=\sqrt{6^2+8^2}\\ \Rightarrow BC=10\)
Áp dụng HTL ta có: \(x.BC=AB^2\Rightarrow x.10=6^2\Rightarrow x=3,6\)
Áp dụng HTL ta có: \(x.BC=AC^2\Rightarrow x.10=8^2\Rightarrow x=6,4\)
Đúng 0
Bình luận (0)
câu 5:
x=3,6
y=6,4
câu 6:
không biết
câu 7:
a)ĐKXĐ:
b) ĐKXĐ:
Đúng 0
Bình luận (0)
mn giúp em câu c bài hình với bài 5 nhé ạ. Em cảm ơn trước