NÊU cách dựng góc nhọn A biết cosA=3/4
NT
Những câu hỏi liên quan
cho góc nhọn a . tính B = sina + cosa biết tana + cota = 3
Hãy nêu cách dựng góc nhọn β theo hình 18 và chứng minh cách dựng đó là đúng.
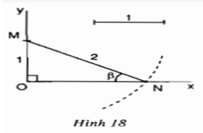
- Dựng đoạn OM trên trục Oy sao cho OM = 1
- Dựng đường tròn tâm M bán kính bằng 2, đường tròn giao với tia Ox tại N
- Khi đó góc MNO là góc cần dựng
Chứng minh:
Tam giác MON vuông tại O có: MO = 1; MN = 2
Khi đó:
sinβ = sin(MNO) = MO/MN = 1/2 = 0,5
Đúng 0
Bình luận (0)
Hãy nêu cách dựng góc nhọn β theo hình 18 và chứng minh cách dựng đó là đúng.
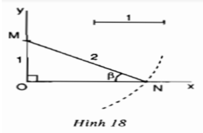
- Dựng đoạn OM trên trục Oy sao cho OM = 1
- Dựng đường tròn tâm M bán kính bằng 2, đường tròn giao với tia Ox tại N
- Khi đó góc MNO là góc cần dựng
Chứng minh:
Tam giác MON vuông tại O có: MO = 1; MN = 2
Khi đó:
sinβ = sin(MNO) = MO/MN = 1/2 = 0,5
Đúng 0
Bình luận (0)
cho góc nhọn a. chứng minh rằng (cosa-sina)2 - (cosa + sina)2 phần cosa.sina = -4
\(\dfrac{\left(cosa-sina\right)^2-\left(cosa+sina\right)^2}{cosa\cdot sina}\)
\(=\dfrac{\left(cosa-sina-cosa-sina\right)\left(cosa-sina+cosa+sina\right)}{cosa\cdot sina}\)
\(=\dfrac{-2\cdot sina\cdot2\cdot cosa}{cosa\cdot sina}=-4\)
Đúng 1
Bình luận (0)
Cho góc nhọn a và cosa =3/4. Không tính số đo góc a, hãy tính sina và tana
\(\cos^2a+sin^2a=1 ;\frac{\sin a}{\cos a}=\tan a\)
Đúng 0
Bình luận (0)
* Cho góc nhọn a. Biết cosa-sina=\(\dfrac{1}{5}\). Tính cota
\(\cos a-\sin a=\dfrac{1}{5}\\ \Leftrightarrow\left(\cos a-\sin a\right)^2=\dfrac{1}{25}\\ \Leftrightarrow1-2\sin a\cos a=\dfrac{1}{25}\\ \Leftrightarrow2\sin a\cos a=\dfrac{24}{25}\)
Mà \(\cos a=\dfrac{1}{5}+\sin a\)
\(\Leftrightarrow2\sin a\left(\dfrac{1}{5}+\sin a\right)=\dfrac{24}{25}\\ \Leftrightarrow\dfrac{2}{5}\sin a+2\sin^2a-\dfrac{24}{25}=0\\ \Leftrightarrow\left[{}\begin{matrix}\sin a=\dfrac{3}{5}\\\sin a=-\dfrac{4}{5}\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}\cos a=\dfrac{4}{5}\\\cos a=-\dfrac{3}{5}\end{matrix}\right.\\ \Leftrightarrow\cot a=\dfrac{4}{5}\cdot\dfrac{5}{3}=\dfrac{4}{3}\)
Đúng 3
Bình luận (1)
Cho góc xOy nhọn, điểm M nằm trong góc. Nêu cách dựng điểm A thuộc Ox, điểm B thuộc Oy sao cho M là trọng tâm tam giác ABC
Bài 6. Cho góc nhọn a. Biết cosa - sina = \(\dfrac{1}{5}\). Tính cot a
Ta có: \(sin^2\alpha+cos^2\alpha=1\Rightarrow sin^2\alpha+\left(sin\alpha+\dfrac{1}{5}\right)^2=1\)
\(\Rightarrow25sin^2\alpha+5sin\alpha-12=0\\\Rightarrow\left(5sin\alpha-3\right)\left(5sin\alpha+4\right)=0\\ \Rightarrow\left[{}\begin{matrix}sin\alpha=\dfrac{3}{5}\Rightarrow cos\alpha=\dfrac{3}{5}+\dfrac{1}{5}=\dfrac{4}{5}\Rightarrow cot\alpha=\dfrac{4}{5}:\dfrac{3}{5}=\dfrac{4}{3}\\sin\alpha=-\dfrac{4}{5}\left(loại\right)\end{matrix}\right. \)
Đúng 2
Bình luận (0)
vẽ hình và nêu cách dựng hình chữ nhật ABCD biết nửa chu vi bằng 5 cm và góc nhọn tạo bởi 2 đường chéo bằng 70 độ




