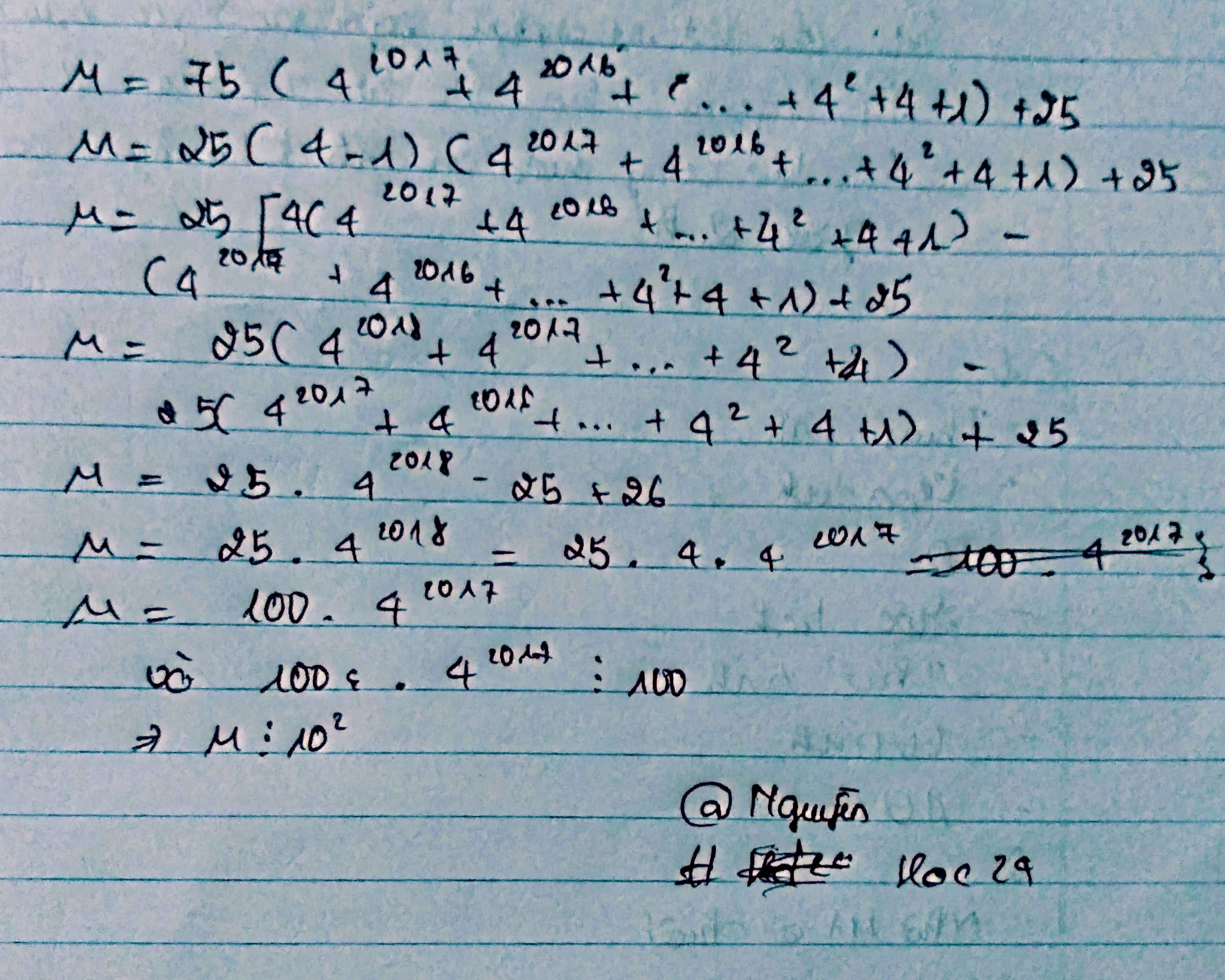2. Chứng tỏ rằng M=75.(42021+42020+....+42+4+1)+ 25 chia hết cho 100
BP
Những câu hỏi liên quan
chứng minh rằng M chia hết cho 100
M=75(42021+42020+...+42+4+1
Ta có M ⋮ 25 vì 75 ⋮ 25
Lại có M = 75 ( 42021 + 42020 + ... + 42 + 4 + 1 )
= 75 . 4 ( 22020 + 22019 + ... + 4 + 1 + 0,25 ) ⋮ 4 vì 4 ⋮ 4
Mà ( 25; 4 ) = 1 ⇒ M ⋮ 100
Vậy M ⋮ 100
Đúng 2
Bình luận (0)
cho biểu thức A=5+42+43+...+42020+42021. Chứng minh 3A+1 chia hết cho 42021
Chứng tỏ rằng :
A = 75 . ( 42004 + 42003 + ...... + 42 + 4 + 1 ) + 25 là số chia hết cho 100
chứng tỏ rằng A=1 cộng 4 cộng 42 cộng 43 cộng ... cộng 42021 chia hết cho 21
A = 1 + 4 + 42 + 43 + ... + 42021
A = 40 + 41 + 42 + 43 +...+ 42021
Xét dãy số 0; 1; 2; 3;...; 2021
Dãy số trên có số số hạng là:
(2021 - 0) : 1 + 1 = 2022
Vậy A có 2022 số hạng
vì 2022 : 3 = 674
Vậy ta nhóm 3 số hạng liên tiếp của A thành một nhóm thì khi đó
A = (1 + 4 + 42) + (43 + 44 + 45) +...+ (42019 + 42020 + 42021)
A = (1 + 4 + 16) + 43.(1 + 4 + 42) + ... +42019.(1 + 4 + 42)
A = 21 + 43.21 +... + 42019.21
A = 21.(1 + 43 + ... + 42019)
21 ⋮ 21 ⇒ 21.(1 + 43 + ...+ 42019) ⋮ 21 ⇒ A ⋮ 21 (đpcm)
Đúng 1
Bình luận (0)
Giải thích các bước giải:
A = 1 + 4 + 42 + 43 + ... + 42021
A = 40 + 41 + 42 + 43 +...+ 42021
Xét dãy số 0; 1; 2; 3;...; 2021
Dãy số trên có số số hạng là:
(2021 - 0) : 1 + 1 = 2022
Vậy A có 2022 số hạng
vì 2022 : 3 = 674
Vậy ta nhóm 3 số hạng liên tiếp của A thành một nhóm thì khi đó ta sẽ có
A = (1 + 4 + 42) + (43 + 44 + 45) +...+ (42019 + 42020 + 42021)
A = (1 + 4 + 16) + 43.(1 + 4 + 42) + ... +42019.(1 + 4 + 42)
A = 21 + 43.21 +... + 42019.21
A = 21.(1 + 43 + ... + 42019)
21 ⋮ 21 ⇒ 21.(1 + 43 + ...+ 42019) ⋮ 21 ⇒ A ⋮ 21 (đpcm)
Vậy ta có thể biết A có thể chia hết cho 21 qua: 1+4+42+43+...+42021
Đúng 0
Bình luận (0)
A, Chứng tỏ rằng: M = 75.(42017+ 42016 +42 +4 + 1) +25 chia hết cho 10² 6+.
2.Chứng tỏ rằng M=\(75.\left(4^{2021}+4^{2020}+...4^2+4+1\right)\)+25 chia hết cho 100
Lời giải:
Xét $A=4^{2021}+4^{2020}+...+4^2+4+1$
$4A=4^{2022}+4^{2021}+...+4^3+4^2+4$
$\Rightarrow 4A-A=4^{2022}-1$
$\Rightarrow 3A=4^{2022}-1$
$\Rightarrow M=75A+25=25(4^{2022}-1)+25=25.4^{2022}=100.4^{2021}\vdots 100$
Ta có đpcm.
Đúng 2
Bình luận (0)
Chứng tỏ rằng A= 75( 4^2023+ 4^2022+4^2021+...+ 4^2+ 4+ 1)+ 25 chia hết cho 100
Đặt \(A=75\left(4^{2023}+4^{2022}+...+4^2+4+1\right)+25\)
Đặt \(B=4^{2023}+4^{2022}+...+4^2+4+1\)
=>\(4B=4^{2024}+4^{2023}+...+4^3+4^2+4\)
=>\(4B-B=4^{2024}+4^{2023}+...+4^3+4^2+4-4^{2023}-4^{2022}-...-4^2-4-1\)
=>\(3B=4^{2024}-1\)
=>\(B=\dfrac{4^{2024}-1}{3}\)
\(A=75\left(4^{2023}+4^{2022}+...+4^2+4+1\right)+25\)
\(=75\cdot\dfrac{4^{2024}-1}{3}+25\)
\(=25\cdot\left(4^{2024}-1\right)+25\)
\(=25\cdot4^{2024}\)
\(=25\cdot4\cdot4^{2023}=100\cdot4^{2023}⋮100\)
Đúng 0
Bình luận (0)
Chứng tỏ rằng \(M=75.\left(4^{2017}+4^{2016}+...+4^2+4+1\right)+25\) chia hết cho 102
Chứng tỏ rằng: A=75×(42004+42003+...+42+4+1)+25
là số chia hết cho 100