giups minhf baif 4
PD
Những câu hỏi liên quan
giups em baif nafy ạ
Cacs banj owi giups minhf vowis mays minhf ko ddanhs daaus ddc!
Minhf ko vieets ddc daaus banj owi!
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
|x-5|-|2x-4|=0
moij nguwowif giair giups minhf vowi
|x - 5| - |2x - 4| = 0
<=> |x - 5| = 0 + |2x - 4|
<=> |x - 5| = |2x - 4|
Xét 2 trường hợp: 2x - 4 = x - 5
2x - 4 = -(x - 5)
TH1: 2x - 4 = x - 5
<=> 2x - 4 - x = -5
<=> x - 4 = -5
<=> x = -5 + 4
<=> x = -1
TH2: 2x - 4 = -(x - 5)
<=> 2x - 4 = -x + 5
<=> 2x - 4 + x = 5
<=> 3x - 4 = 5
<=> 3x = 5 + 4
<=> 3x = 9
<=> x = 3
=> x = 3
Vậy: x = -1 hoặc x = 3
Đúng 0
Bình luận (0)
giups minhf
1 The Temple of Literature is about 10 minutes away from Hoan Kiem Lake
2 There are five courtyards
3 It''s used for street signs of Ha Noi
4 We can find the stone tablets above tortoise backs with thenames of doctors in the third courtyard
EX4
1 : My town was visited by hundreds of tourists last year
Đúng 1
Bình luận (2)
Xem chi tiết
PN
17 tháng 11 2021 lúc 18:58
giups minhf voiws
giups minhf vs aj
giups minhf voiws cacs banj!!!! 🙏😭🥺
Xem thêm câu trả lời
GIAIR DDAAYF DDUR GIUPS MINHF VOIWS AJ
MINHF CAMR OWN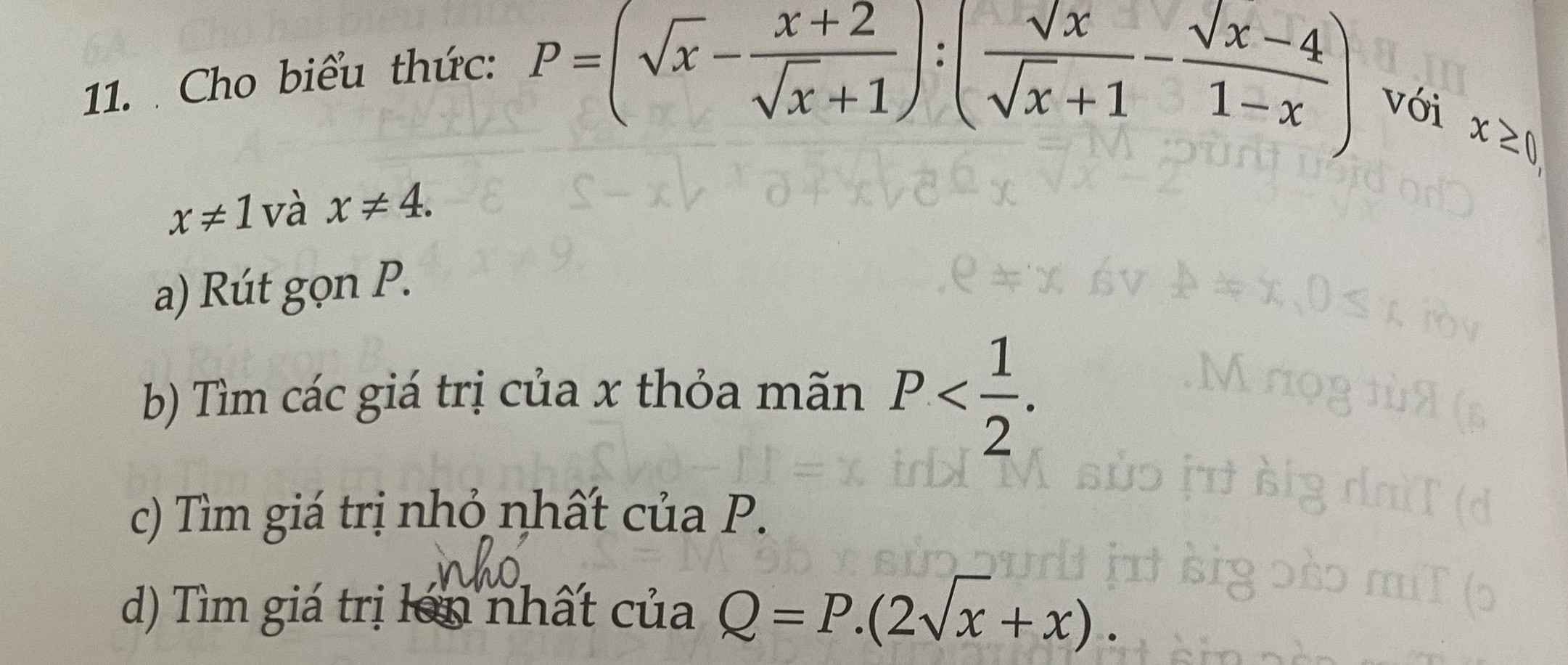
a, \(P=\left(\sqrt{x}-\dfrac{x+2}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}-\dfrac{\sqrt{x}-4}{1-x}\right)\)
\(=\left(\dfrac{x+\sqrt{x}}{\sqrt{x}+1}-\dfrac{x+2}{\sqrt{x}+1}\right):\left[\dfrac{\sqrt{x}\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}+\dfrac{\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\right]\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}:\dfrac{x-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-2}{\sqrt{x}+1}.\dfrac{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}{\left(\sqrt{x}+2\right)\left(\sqrt{x}-2\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
Đúng 1
Bình luận (0)
b, \(P< \dfrac{1}{2}\Leftrightarrow\dfrac{\sqrt{x}-1}{\sqrt{x}+2}< \dfrac{1}{2}\)
\(\Leftrightarrow2\sqrt{x}-2< \sqrt{x}+2\)
\(\Leftrightarrow\sqrt{x}< 4\)
\(\Leftrightarrow0\le x< 16\)
Vậy \(0\le x< 16;x\ne1;x\ne4\).
Đúng 0
Bình luận (0)
a: ta có: \(P=\left(\sqrt{x}-\dfrac{x+2}{\sqrt{x}+1}\right):\left(\dfrac{\sqrt{x}}{\sqrt{x}+1}+\dfrac{\sqrt{x}-4}{x-1}\right)\)
\(=\dfrac{x+\sqrt{x}-x-2}{\left(\sqrt{x}+1\right)}:\dfrac{x-\sqrt{x}+\sqrt{x}-4}{\left(\sqrt{x}+1\right)\left(\sqrt{x}-1\right)}\)
\(=\dfrac{\sqrt{x}-2}{1}\cdot\dfrac{\sqrt{x}-1}{\left(\sqrt{x}-2\right)\left(\sqrt{x}+2\right)}\)
\(=\dfrac{\sqrt{x}-1}{\sqrt{x}+2}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời