`b)2x^2-5x+2=0`

`<=>2x^2-4x-x+2=0`

`<=>(x-2)(2x-1)=0`

`<=>[(x=2),(x=1/2):}`

`d)12x^2-53x+20=0`

`<=>12x^2-48x-5x+20=0`

`<=>(x-4)(12x-5)=0`

`<=>[(x=4),(x=5/12):}`

\(b,2x^2-5x+2=0\\ \Leftrightarrow2x^2-4x-x+2=0\\ \Leftrightarrow2x\left(x-2\right)-\left(x-2\right)=0\\ \Leftrightarrow\left(2x-1\right)\left(x-2\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}2x-1=0\\x-2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{1}{2}\\x=2\end{matrix}\right.\\ d,12x^2-53x+20=0\\ \Leftrightarrow12x^2-48x-5x+20=0\\ \Leftrightarrow12x\left(x-4\right)-5\left(x-4\right)=0\\ \Leftrightarrow\left(12x-5\right)\left(x-4\right)=0\\ \Leftrightarrow\left[{}\begin{matrix}12x-5=0\\x-4=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{5}{12}\\x=4\end{matrix}\right.\)

\(\sqrt{2023-\sqrt{x}}=2023-x\left(ĐK:x\ge0\right)\)

Đặt \(t=\sqrt{x}\left(t\le2023\right)\)

Pt trở thành : \(\sqrt{2023-t}=2023-t^2\)

\(\Leftrightarrow2023-t=\left(2023-t^2\right)^2\)

\(\Leftrightarrow t^4-4046t+4092529=2023-t\)

\(\Leftrightarrow t^4-4045+4090506=0\)

\(\Leftrightarrow\left[{}\begin{matrix}t=2023\left(n\right)\\t=2022\left(n\right)\end{matrix}\right.\)

+) Với \(t=2023\Rightarrow x^2=2023\Rightarrow x=\pm17\sqrt{7}\)

+) Với \(t=2022\Rightarrow x^2=2022\Leftrightarrow x=\pm\sqrt{2022}\)

Vì \(x\ge0\) \(\Rightarrow x\in\left\{17\sqrt{7};\sqrt{2022}\right\}\)

Vậy \(S=\left\{17\sqrt{7};\sqrt{2022}\right\}\)

Câu 1: 

a) Ta có: 7x+21=0

\(\Leftrightarrow7x=-21\)

hay x=-3

Vậy: S={-3}

b) Ta có: 3x-2=2x-3

\(\Leftrightarrow3x-2-2x+3=0\)

\(\Leftrightarrow x+1=0\)

hay x=-1

Vậy: S={-1}

c) Ta có: 5x-2x-24=0

\(\Leftrightarrow3x=24\)

hay x=8

Vậy: S={8}

Câu 2: 

a) Ta có: \(\left(2x+1\right)\left(x-1\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x+1=0\\x-1=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=-1\\x=1\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-\dfrac{1}{2}\\x=1\end{matrix}\right.\)

Vậy: \(S=\left\{-\dfrac{1}{2};1\right\}\)

b) Ta có: \(\left(2x-3\right)\left(-x+7\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}2x-3=0\\-x+7=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}2x=3\\-x=-7\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=\dfrac{3}{2}\\x=7\end{matrix}\right.\)

Vậy: \(S=\left\{\dfrac{3}{2};7\right\}\)

c) Ta có: \(\left(x+3\right)^3-9\left(x+3\right)=0\)

\(\Leftrightarrow\left(x+3\right)\left[\left(x+3\right)^2-9\right]=0\)

\(\Leftrightarrow\left(x+3\right)\left(x+3-3\right)\left(x+3+3\right)=0\)

\(\Leftrightarrow x\left(x+3\right)\left(x+6\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}x=0\\x+3=0\\x+6=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=0\\x=-3\\x=-6\end{matrix}\right.\)

Vậy: S={0;-3;-6}

\(\Leftrightarrow\left[{}\begin{matrix}x\left(x+1\right)=x+1\\x\left(x+1\right)=-\left(x+1\right)\end{matrix}\right.\Leftrightarrow}\left[{}\begin{matrix}\left(x+1\right)\left(x-1\right)=0\\\left(x+1\right)^2=0\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=-1\\x=1\end{matrix}\right.\)

b: ĐKXD: x<>1/5; x<>3

PT\(\Leftrightarrow\dfrac{3}{5x-1}-\dfrac{2}{x-3}=\dfrac{-4}{\left(5x-1\right)\left(x-3\right)}\)

=>3x-9-10x+2=-4

=>-7x-7=-4

=>-7x=3

=>x=-3/7

a: ĐKXĐ: x<>2/3; x<>-2/3

\(PT\Leftrightarrow\left(3x+2\right)^2-6\left(3x-2\right)=9x\)

=>9x^2+12x+4-18x+12-9x=0

=>9x^2-15x+16=0

=>\(x\in\varnothing\)

c: ĐKXĐ: x<>1/4; x<>-1/4

PT =>-3(4x+1)=2(4x-1)-6x-8

=>-12x-3=8x-2-6x-8

=>-12x-3=2x-10

=>-14x=-7

=>x=1/2

d: ĐKXĐ: x<>0; x<>2

\(\Leftrightarrow\dfrac{5-x}{4x\left(x-2\right)}+\dfrac{7}{8x}=\dfrac{x-1}{2x\left(x-2\right)}+\dfrac{1}{8\left(x-2\right)}\)

=>2(5-x)+7(x-2)=4(x-1)+x

=>10-2x+7x-14=4x-4+x

=>5x-4=5x-4

=>0x=0(luôn đung)

Vậy: S=R\{0;2}

e: DKXĐ: x<>0

PT \(\Leftrightarrow\dfrac{\left(x+1\right)\left(x^2-x+1\right)-\left(x-1\right)\left(x^2+x+1\right)}{\left(x^2+x+1\right)\left(x^2-x+1\right)}=\dfrac{3}{x\left(x^2+x+1\right)\left(x^2-x+1\right)}\)

=>x(x^3+1-x^3+1)=3

=>2x=3

=>x=3/2

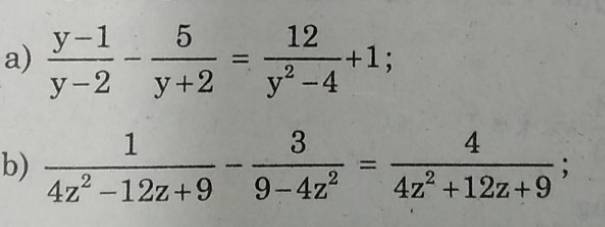
\(a,\dfrac{y-1}{y-2}-\dfrac{5}{y+2}=\dfrac{12}{y^2-4}+1\left(ĐKXĐ:x\ne\pm2\right)\)

\(\Leftrightarrow\dfrac{\left(y-1\right)\left(y+2\right)}{\left(y-2\right)\left(y+2\right)}-\dfrac{5\left(y-2\right)}{\left(y-2\right)\left(y+2\right)}-\dfrac{12}{\left(y-2\right)\left(y+2\right)}-\dfrac{\left(y-2\right)\left(y+2\right)}{\left(y-2\right)\left(y+2\right)}=0\)

\(\Leftrightarrow\dfrac{y^2+y-2}{\left(y-2\right)\left(y+2\right)}-\dfrac{5y-10}{\left(y-2\right)\left(y+2\right)}-\dfrac{12}{\left(y-2\right)\left(y+2\right)}-\dfrac{y^2-4}{\left(y-2\right)\left(y+2\right)}=0\)

\(\Leftrightarrow\dfrac{y^2+y-2-5y+10-12-y^2+4}{\left(y-2\right)\left(y+2\right)}=0\)

\(\Rightarrow-4y=0\)

\(\Leftrightarrow y=0\left(tm\right)\)

\(b,\dfrac{1}{4z^2-12z+9}-\dfrac{3}{9-4z^2}=\dfrac{4}{4z^2+12z+9}\left(ĐKXĐ:z\ne\pm\dfrac{3}{2}\right)\)

\(\Leftrightarrow\dfrac{1}{\left(2z-3\right)^2}+\dfrac{3}{\left(2z-3\right)\left(2z+3\right)}-\dfrac{4}{\left(2z+3\right)^2}=0\)

\(⇔\dfrac{\left(2z+3\right)^2}{\left(2z-3\right)^2\left(2z+3\right)^2}+\dfrac{3\left(2z-3\right)\left(2z+3\right)}{\left(2z-3\right)^2\left(2z+3\right)^2}-\dfrac{4\left(2z-3\right)^2}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)

\(\Leftrightarrow\dfrac{4z^2+12z+9}{\left(2z-3\right)^2\left(2z+3\right)^2}+\dfrac{12z^2-27}{\left(2z-3\right)^2\left(2z+3\right)^2}-\dfrac{16z^2-48z+36}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)

\(\Leftrightarrow\dfrac{4z^2+12z+9+12z^2-27-16z^2+48z-36}{\left(2z-3\right)^2\left(2z+3\right)^2}=0\)

\(\Rightarrow60z-54=0\)

\(\Leftrightarrow60z=54\)

\(\Leftrightarrow z=\dfrac{9}{10}\left(tm\right).\)

\(a,\dfrac{y-1}{y-2}-\dfrac{5}{y+2}=\dfrac{12}{y^2-4}+1\left(dkxd:y\ne\pm2\right)\)

\(\Leftrightarrow\dfrac{\left(y-1\right)\left(y+2\right)-5\left(y-2\right)-12-y^2+4}{y^2-4}=0\)
\(\Leftrightarrow y^2+2y-y-2-5y+10-12-y^2+4=0\)

\(\Leftrightarrow-4y=0\)

\(\Leftrightarrow y=0\left(tmdk\right)\)

Vậy \(S=\left\{0\right\}\)

\(b,\dfrac{1}{4z^2-12z+9}-\dfrac{3}{9-4z^2}=\dfrac{4}{4z^2+12z+9}\)

\(\Leftrightarrow\dfrac{1}{\left(2z-3\right)^2}-\dfrac{3}{\left(2z-3\right)\left(2z+3\right)}=\dfrac{4}{\left(2z+3\right)^2}\left(dkxd:z\ne\pm\dfrac{3}{2}\right)\)

\(\Leftrightarrow\left(2z+3\right)^2-3\left(4z^2-9\right)-4\left(2z-3\right)^2=0\)

\(\Leftrightarrow4z^2+12z+9-12z^2+27-4\left(4z^2-12z+9\right)=0\)

\(\Leftrightarrow4z^2+12z+9-12z^2+27-16z^2+48z-36=0\)

\(\Leftrightarrow-24z^2+60z=0\)

\(\Leftrightarrow-12z\left(2z-5\right)=0\)

\(\Leftrightarrow\left[{}\begin{matrix}-12z=0\\2z-5=0\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}z=0\left(tmdk\right)\\z=\dfrac{5}{2}\left(tmdk\right)\end{matrix}\right.\)

Vậy \(S=\left\{0;\dfrac{5}{2}\right\}\)

\(\left\{{}\begin{matrix}3x-2y=-2\\2x+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}3x-2y=-2\\4x+2y=2\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}7x=0\\2x+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\2.0+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\0+y=1\end{matrix}\right.\) \(\Leftrightarrow\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)

Vậy...

\(\left\{{}\begin{matrix}3x-2y=-2\\2x+y=1\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}3x-2y=-2\\4x+2y=2\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}7x=0\\2x+y=1\end{matrix}\right.\)⇔\(\left\{{}\begin{matrix}x=0\\2.0+y=1\end{matrix}\right.\)

⇔\(\left\{{}\begin{matrix}x=0\\y=1\end{matrix}\right.\)

vậy...

(x²-3x+2)(x²​-9x+20)=40

=>x=0 hoặc 6

\(x^2+2y^2-2xy+y=0\) đề phải như thế này chứ