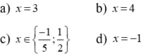Giải phương trình:
4x2 + 1/2x -1 = √(4x-1)
H24
Những câu hỏi liên quan
Giải phương trình:
4x2 + 1/2x -1 = √(4x-1)
Giải phương trình:
4x2 + 1/2x -1 = √(4x-1)
Giải phương trình:
4x2 + 1/2x -1 = √(4x-1)
Giải phương trình:
4x2 + 1/2x -1 = √(4x-1)
Giải phương trình:
4x2 + 1/2x -1 = √(4x-1)
Giải phương trình 2 x + 3 + 4 x 2 + 9 x + 2 = 2 x + 2 + 4 x + 1 .
Pt ⇔ 2 x + 3 + ( x + 2 ) ( 4 x + 1 ) = 2 x + 2 + 4 x + 1 . ĐK: x ≥ − 1 4
Đặt t 2 = 8 x + 4 ( x + 2 ) ( 4 x + 1 ) + 9 ⇔ 2 x + ( x + 2 ) ( 4 x + 1 ) = t 2 − 9 4
PTTT t 2 − 4 t + 3 = 0 ⇔ t = 1 hoặc t = 3
TH1. t = 1 giải ra vô nghiệm hoặc kết hợp với ĐK t ≥ 7 bị loại
TH 2 t = 3 ⇒ 2 x + 2 + 4 x + 1 = 3. Giải pt tìm được x = − 2 9 (TM)
Vậy pt có nghiệm duy nhất x = − 2 9
Đúng 0
Bình luận (0)
\(x=1,0572\)
Giải phương trình :
a
)
(
2
x
–
1
)
(
4
x
2
+
2
x
+
1
)
–
4
x
(
2
x
2
–
3
)
23...
Đọc tiếp
Giải phương trình :
a ) ( 2 x – 1 ) ( 4 x 2 + 2 x + 1 ) – 4 x ( 2 x 2 – 3 ) = 23
b ) x + 2 x + 1 - 1 x - 2 = 1 - 3 x 2 - x - 2
a) (2x – 1)(4x2 + 2x + 1) – 4x(2x2 – 3) = 23
⇔ 8x3 – 1 – 8x3 + 12x = 23
⇔ 12x = 24 ⇔ x = 2.
Tập nghiệm của phương trình: S = {2}
b) ĐKXĐ : x + 1 ≠ 0 và x – 2 ≠ 0 (vì vậy x2 – x – 2 = (x + 1)(x – 2) ≠ 0)
⇔ x ≠ -1 và x ≠ 2
Quy đồng mẫu thức hai vế :
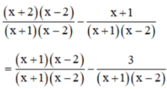
Khử mẫu, ta được : x2 – 4 – x – 1 = x2 – x – 2 – 3 ⇔ 0x = 0
Phương trình này luôn nghiệm đúng với mọi x ≠ -1 và x ≠ 2.
Đúng 0
Bình luận (0)
Giải các phương trình sau:a)
9
−
x
2
x
;
b)
x
−
15
+
1
3
x
;
c)
4
x
2
−
1
+
3
x...
Đọc tiếp
Giải các phương trình sau:
a) 9 − x = 2 x ; b) x − 15 + 1 = 3 x ;
c) 4 x 2 − 1 + 3 x 2 x − 1 = 0 ; d) 5 − 4 x = 4 − 5 x .
Giải phương trình: 4x2 + 4x + 1 = x2.
4x2 + 4x + 1 = x2
⇔ 4x2 + 4x + 1 – x2 = 0
⇔ (4x2 + 4x + 1) – x2 = 0
⇔ (2x + 1)2 – x2 = 0
⇔ (2x + 1 – x)(2x + 1 + x) = 0
(Sử dụng hằng đẳng thức)
⇔ (x + 1)(3x + 1) = 0
⇔ x + 1 = 0 hoặc 3x + 1 = 0
+ x + 1 = 0 ⇔ x = -1.
+ 3x + 1 = 0 ⇔ 3x = -1 ⇔ 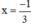
Vậy phương trình có tập nghiệm 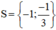
Đúng 0
Bình luận (0)