Vẽ \(\Delta\)ABC. Giả sử govs B=350, góc C=550. \(\Delta\) ABC là tam giác gì
ai nhanh mik cho 3k
vẽ tam giác ABC. giả sử góc ABC=80 độ, góc ACB=40 độ. Hai tia phân giác kẻ từ đỉnh B và C cắt nhau tại I. Tính IBC+ICB và tính BIC
ai nhanh mik tick 3k
vì BI là tia phân giác của ^ABC => ^ ABI = ^ IBC= ^ ABC / 2 = 80 / 2 =40
=>^IBC=40
vì CI là tia phân giác của ^ACB => ^ACI = ^ ICB = ACB / 2 = 40 / 2 = 20
=>^ICB = 20
Ta có : ^BIC+^IBC+^ICB= 180 ( tổng ba góc của 1 tam giác )
=> ^BIC +40+20 =180
=>^BIC = 120
Vẽ tam gác ABC có đường phân giác AD. Giả sử góc B=75 dộ; góc C=75 độ. Tính góc BAD
ai nhanh 3k
Hí hí, hey Phương
Kết quả là:
= 15o
nha ~~
~Bài của thầy Kì à~
Tam giác ABC: B^ = C^ = 75o ; A^ +B^ +C^ = 180o = A^ + 150 = 180o => A^ = 30o
BAD^ = A^/2 = 15o
Góc A bằng:
180-75-75=30(độ)
Góc BAD bằng:
30:2=15(độ)
Đáp số: 15 độ
\(\Delta\)ABC có góc A = 90độ. Vẽ phân giác góc B cắt AC tại D. Vẽ DE vuông góc BC
a) C/m \(\Delta ABD=\Delta EBD\)
b) vẽ tia đối của tia DE cắt BA tại F. C/m AE song song CF
c) Giả sử góc ABC= 60độ. Khi đó \(\Delta ABE\) là tam giác gì? Vì sao?
Mọi người giải hộ mình với. Mình cần bài này gấp !!!!
a)xét tam gác ABD và EBD có
góc ABP=EBP
PB là cạnh chung
góc A=E=90độ
ABD = EBD(cạnh huyền góc nhọn)
a) Cho \(\Delta ABC\)và R là bán kính đường tròn ngoại tiếp tam giác thỏa mãn \(R\left(b+c\right)=a\sqrt{bc}\). Xác định hình dạng tam giác b) Giả sử \(\Delta ABC\)không có góc tù vfa có 2 đường sao AH, BK sao cho \(AH\ge BC\); \(BK\ge AC\). Tính các góc \(\Delta ABC\)
vẽ tam giác ABC nhọn có đường cao AH. Vẽ HI vuông góc với AC ở I
1) chứng minh AHI=C
2) giả sử B=75 độ; BAC = 65 độ. Tính AHI
ai nhanh 3k
Đường cao AH vuông góc với BC tại H,HI vuông góc AC tại I
=>\(\Delta AHI,\Delta AHC\)có\(90^0=\widehat{A}+\widehat{AHI}=\widehat{A}+\widehat{C}\Rightarrow\widehat{AHI}=\widehat{C}\)
\(\Delta ABC\)có\(\widehat{C}=180^0-\widehat{B}-\widehat{BAC}=180^0-75^0-65^0=40^0\)mà\(\widehat{AHI}=\widehat{C}\left(cmt\right)\Rightarrow\widehat{AHI}=40^0\)
a) Ta có: AHI^ + IHC^ = 90o => AHI^ = 90o - IHC^
Tam giác HIC: ICH^ = 90o - IHC^
=> AHI^ = ICH^ hay AHI^ = C^ (1)
b) Tam giác ABC: ABC^ + BAC^ + ACB^ = 180o => ACB^ = 180o - ABC^ - BAC^ = 180o - 75o - 65o = 40o (2)
Từ (1) và (2) => AHI^ = 40o
Cho \(\Delta ABC\)cân tại A ( góc A < 90 độ). Kẻ BD \(\perp\)AC tại D. Trên cạnh AB lấy E sao cho AE=AD. Gọi I là giao điểm của BD và CE. Chứng minh rằng:
a. \(\Delta ABD=\Delta ACE\)và CE \(\perp\)AB
b. AI là tia phân giác của góc BAC
c.\(\Delta IBC\)là tam giác cân
d. Gọi H là giao điểm của AI và DE. Giả sử \(\Delta ABC\)là tam giác đều và AB=12cm. Tính CE và AH?
cho \(\Delta ABC\) có \(\widehat A={40^0}\) biết \(\widehat B= 3\widehat C\) tam giác abc là tam giác gì
giúp mik với
\(\widehat{B}+\widehat{C}=140^0\)
\(\Leftrightarrow4\cdot\widehat{C}=140^0\)
\(\Leftrightarrow\widehat{C}=35^0\)
hay \(\widehat{B}=105^0\)
Vậy: ΔABC tù
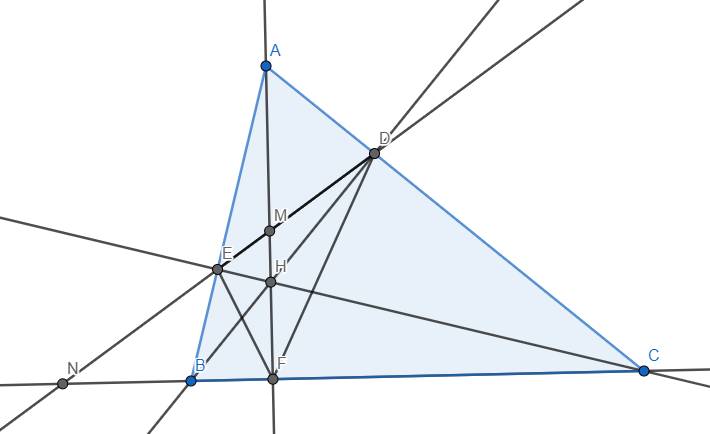
Cho ΔABC nhọn, AB<AC. Đường cao BD, CE cắt nhau ở H
a)Chứng minh: \(AE\cdot AB=AD\cdot AC\)
b)Chứng minh: \(\Delta ADE\)ᔕ\(\Delta ABC\)
c)Giả sử góc BAC=45 độ
Tính tỉ số diện tích \(\Delta ADE\) với diện tích tứ giác BEDC
d)Gọi M, N lần lượt là giao điểm của DE với AH và BC
Chứng minh: \(MD\cdot NE=ME\cdot ND\)
a) Xét \(\Delta ABD\) và \(\Delta ACE\), ta có \(\widehat{ADB}=\widehat{AEC}\left(=90^o\right)\) và góc A chung \(\Rightarrow\Delta ABD~\Delta ACE\left(g.g\right)\) \(\Rightarrow\dfrac{AB}{AC}=\dfrac{AD}{AE}\) \(\Rightarrowđpcm\)
b) Từ \(AE.AB=AD.AC\Rightarrow\dfrac{AD}{AB}=\dfrac{AE}{AC}\)
Xét \(\Delta ADE\) và \(\Delta ABC\), ta có \(\dfrac{AD}{AB}=\dfrac{AE}{AC}\) và góc A chung \(\Rightarrowđpcm\)
c) Do \(\Delta ADE~\Delta ABC\) \(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{AD}{AB}\right)^2\)
Lại có \(\dfrac{AD}{AB}=cosA=cos45^o=\dfrac{1}{\sqrt{2}}\) nên \(\dfrac{S_{ADE}}{S_{ABC}}=\left(\dfrac{1}{\sqrt{2}}\right)^2=\dfrac{1}{2}\)\(\Rightarrow\dfrac{S_{ADE}}{S_{ABC}-S_{ADE}}=\dfrac{1}{2-1}\) \(\Rightarrow\dfrac{S_{ADE}}{S_{BEDC}}=1\)
d) Kẻ đường cao AF của tam giác ABC. Tương tự câu b, ta chứng minh được các tam giác BFE và CDF cùng đồng dạng với tam giác ABC. Từ đó suy ra \(\Delta BEF~\Delta DCF\) \(\Rightarrow\widehat{BFE}=\widehat{CFD}\) \(\Rightarrow90^o-\widehat{BFE}=90^o-\widehat{CFD}\) \(\Rightarrow\widehat{EFM}=\widehat{DFM}\) \(\Rightarrow\) FM là tia phân giác trong tam giác DEF \(\Rightarrow\dfrac{MD}{ME}=\dfrac{FD}{FE}\).
Mặt khác, \(FN\perp FM\) \(\Rightarrow\) FN là phân giác ngoài của tam giác DEF \(\Rightarrow\dfrac{ND}{NE}=\dfrac{FD}{FE}\). Từ đó suy ra \(\dfrac{MD}{ME}=\dfrac{ND}{NE}\) \(\Rightarrowđpcm\)
Cho tam giác ABC vuông có AB = 9cm , AC = 12cm . Vẽ phân giác BD
a) Tính BD , AD
b) Qua D vẽ đường thẳng vuông góc với BC tại H , cắt tia BA tại E . chứng minh \(\Delta ABC\) đồng dạng \(\Delta HDC\) . Tính diện tích \(\Delta ADE\)
Xin lỗi mấy bạn . Mình bị thiếu chỗ (cho tam giác ABC vuông tại A)