tìm các cặp ( x,y) thỏa mãn: 5x2 + y2 - 2xy + 2x - 6y +1 < 0
NL
Những câu hỏi liên quan
tìm các cặp ( x,y) thỏa mãn: 5x2 + y2 - 2xy + 2x - 6y +1 < 0
(2x+2y)^2+(x-1)^2+(y+1)^2=0
(2x+2y)^2=0và (x-1)^2=0 và (y+1)^2 cũng =0
(x-1)^2=0
x-1=0
x=1
(y+1)^2
y+1=0
y=-1
x=1
y=-1
nhaaaaaaaaaaaaaaaaaaaaa
Đúng 0
Bình luận (0)
tìm các cặp ( x,y) thỏa mãn: 5x2 + y2 - 2xy + 2x - 6y +1 < 0
tìm các cặp ( x,y) thỏa mãn: 5x2 + y2 - 2xy + 2x - 6y +1 < 0
Cần gấp lắm nha
mk bt bài nầy kb vs mk đi mk trả lời cho
Đúng 0
Bình luận (0)
Trong tất cả các cặp số (x,y) thỏa mãn
log
x
2
+
y
2
+
3
(
2
x
+
2
y
+
5
)
≥
1
giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m 0 thuộc tập nào sau đây?
Đọc tiếp
Trong tất cả các cặp số (x,y) thỏa mãn log x 2 + y 2 + 3 ( 2 x + 2 y + 5 ) ≥ 1 giá trị thực của m để tồn tại duy nhất cặp (x,y) sao cho x2 + y2 + 4x + 6y + 13 - m = 0 thuộc tập nào sau đây?
Đáp án A
Ta có, giả thiết
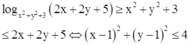
là miền trong đường tròn tâm I(1;1) bán kính R1 = 2
Và
Đúng 0
Bình luận (0)
Bài 1 Tìm cặp số (x;y) thỏa mãn biểu thức sau
2x^2+y^2-2xy-10x+6y+13=0
x^2+7y^2-4xy-2x-2y+4=0
11x^2+y^2-6xy-14x+2y+9=0
Ttìm cặp số x, y nguyên thỏa mãn 5x^2 +y^2 -2xy+2x-6y+1<0
Tìm cặp số x,y thỏa 5x^2 +2y+y^2 -4x-40=0
Giải hệ phương trình sau:
xy(x-y)=2
9xy(3x-y)+6=26x^3 -2y^3
5x2+2y+y2-4x-40=0
△=(-4)2-4.5.(2y+y2-40)
△=16-40y-20y2+800
△=-(784+40y+20y2)
△=-(32y+8y+16y2+4y2+16+4+764)
△=-[(4y+4)2+(2y+2)2+764]<0
=>PHƯƠNG TRÌNH VÔ NGHIỆM.
Đúng 0
Bình luận (0)
Bài 1: Tìm các cặp số nguyên x;y thỏa mãn 2xy+2x-3y+5=0
Tìm các số nguyên x,y thỏa mãn : x2 -3y2+2xy-2x+6y-4=0
\(x^2-3y^2+2xy-2x+6y-4=0\)
\(\Leftrightarrow\left(x-y+1\right)\left(x+3y-3\right)=1\)
Làm nôt
Đúng 0
Bình luận (0)
Viết pt trên thành pt bậc 2 đối với x:\(x^2+2x\left(y-1\right)-\left(3y^2-6y+4\right)=0\) (1)
Pt (1) có nghiệm \(\Leftrightarrow\Delta'=\left(y-1\right)^2+\left(3y^2-6y+4\right)\ge0\)
\(\Leftrightarrow4y^2-8y+5\ge0\),Ta cần có \(\Delta'=k^2\)
Tức là \(4y^2-8y+5=k^2\Leftrightarrow4\left(y-1\right)^2+1=k^2\)
\(\Leftrightarrow\left(2y-2\right)^2-k^2=-1\Leftrightarrow\left(2y-2-k\right)\left(2y-2+k\right)=-1\)
Đến đây bí!
Đúng 0
Bình luận (0)
Tìm các số nguyên x,y thỏa mãn \(x^2-3y^2+2xy-2x+6y-4=0\)