cho tam giác ABC nhọn, có BD đg cao, CE đg cao, 2 đg cao cắt nhau tại H
c/m: BH.BD + CH.CE = BC^2
cho tam giác nhọnABC có đg cao bd và CE cắt tại H
CMR BH.BD+ch.ce=BC2
Kẻ HK vuông góc với BC
Xét tam giác BKH và BCD có góc CBD chung;góc HKB=BDC(90o)
=>Tam giác BKH đồng dạng với BDC
=>BK/BD=BH/BC=>BHxBD(1)
+Tương tụ,tma giác CKH đồng dạng với tg CEB
=>CK/CE=CH/BC=>CHxCE=CK(2)
Từ (1) và (2)=>BHxBD+CHxCE=BKxBC+CKxBC=(BC+CK)xBC=BCxBC=BC2
Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H. Cmr: BH.BD+CH.CE=BC^2
Cho tam giác ABC nhọn, đường cao BD, CE cắt nhau tại H. Chứng minh BH.BD+CH.CE=BC2
Kẻ HM vuông góc BC ( M thuộc BC )
\(\Delta BHM~\Delta BCD\left(g.g\right)\) \(\Rightarrow\frac{BH}{BC}=\frac{BM}{BD}\Rightarrow BH.BD=BC.BM\) ( 1 )
\(\Delta CHM~\Delta CBE\left(g.g\right)\Rightarrow\frac{CH}{BC}=\frac{CM}{CE}\Rightarrow CH.CE=BC.CM\) ( 2 )
Từ ( 1 ) và ( 2 ) \(\Rightarrow BH.BD+CH.CE=BC\left(BM+CM\right)=BC^2\)
Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H.
Chứng minh rằng : BH.BD + CH.CE = BC2.
Kẻ HF vuông góc với BC, F thuộc BC
Ta chứng minh được tg BHF đồng dạng với tg BCD
=> BH/BC = BF/BD => BH.BD=BC.BF
tg CHF đồng dạng với tg CBE
=>CH/CB= CF/CE=CB.CF
=>BH.BD+CH.CE=CB.BF=CB.CB=BC2
Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H.
Chứng minh rằng : BH.BD + CH.CE = BC2.
Kẻ HM | BC
+) Tam giác BHM đồng dạng với tam giác BCD ( có góc BEH = BDC = 90o; góc CBD chung)
=> BM/ BD = BH/ BC => BM. BC = BH. BD (1)
+) Tương tự, tam giác CMH đồng dạng với tam giác CEB ( có góc BCE chung ; góc HMC = CEB = 90o)
=> CH/ CB = CM/ CE =>CM .CB = CH. CE (2)
Cộng từng vế của (1)(2) => BM.BC + CM.CB = BH.BD + CH .CE => (BM + CM).CB = BH.BD + CH.CE
=> BC2 = BH.BD + CH.CE
Vậy...
Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H.
Chứng minh rằng : BH.BD + CH.CE = BC2.
Kẻ HK vuông góc với BC
Xét tam giác BKH và BDC có: góc CBD chung; góc HKB = BDC (= 90o)
=> tam giác BKH đồng dạng với BDC (g - g)
=> BK/BD = BH/ BC => BH.BD = BK. BC (1)
+) Tương tự, tam giác CKH đồng dạng với tam giác CEB (g - g)
=> CK/ CE = CH/BC => CH . CE = CK.BC (2)
Từ (1)(2) => BH.BD + CH.CE = BK.BC + CK. BC = (BK+ CK). BC = BC.BC = BC2
Cho tam giác nhọn ABC có hai đường cao BD và CE cắt nhau tại H.
Chứng minh rằng : BH.BD + CH.CE = BC2.
Xét \(\Delta BHF\)và \(\Delta BCD\)
có \(\widehat{BEH}=\widehat{BDC}=90^0\)và \(\widehat{DBC}\)chung
\(\Rightarrow\Delta BHF~\Delta BCD\left(g-g\right)\)\(\Rightarrow\frac{BF}{BD}=\frac{BH}{BC}\Rightarrow BF.BC=BH.BD\left(1\right)\)
Xét \(\Delta CFH\)và \(\Delta CEB\)
có \(\widehat{CFH}=\widehat{CEB}=90^0\)và \(\widehat{ECB}\)chung
\(\Rightarrow\Delta CFH~\Delta CEB\left(g-g\right)\)\(\Rightarrow\frac{CH}{CB}=\frac{CF}{CE}\Rightarrow CB.CF=CH.CE\left(2\right)\)
Cộng (1) với (2) ta được \(BF.BC+CF.CB=BH.HD+CH.CE\)
\(\Rightarrow\left(BF+CF\right)CB=BH.BD+CH.CE\)hay \(BH.BD+CH.CE=BC^2\left(đpcm\right)\)
Vậy ....
Cho tam giác ABC nhọn, các đường cao BD và CE cắt nhau tại H. Chứng minh
B C 2 = B H . B D + C H . C E .
Gợi ý: Gọi 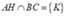 , chứng minh được AK ^ BC.
, chứng minh được AK ^ BC.
Áp dụng cách làm tương tự 4A suy ra ĐPCM