Cho tam giác ABC Có:
A, AB = 5cm , Ac = 7cm ; BC = 8cm Hãy so sánh các góc của tam giác.
B, △Abc có Â = 100độ , B = 300 . Hãy so sánh độ dài 3 cạnh của tam giác đó
HN
Những câu hỏi liên quan
Bài 1: Cho tam giác abc có AB = 5cm AC = 7cm BC = 9cm. Đường phân giác AD. Tính DB, DC
Bài 2: Cho tam giác ABC vuông tại A. AB = 6cm, AC = 8cm, phân giác AD. Tính DB, DC
Xem thêm câu trả lời
cho 2 tam giác ABC và tam giác MNP có AB=7cm;BC=5cm;AC=4cm tính chu vi tam giác MNP
Cho tam giác ABC vuông tại A có AC 7cm, AB 5cm. Tính BC;
C
^
A.
B
C
74
(
c
m
)
;
B
^
≈
35
0
32
B.
B
C
74
(
c
m...
Đọc tiếp
Cho tam giác ABC vuông tại A có AC = 7cm, AB = 5cm. Tính BC; C ^
A. B C = 74 ( c m ) ; B ^ ≈ 35 0 32 '
B. B C = 74 ( c m ) ; B ^ ≈ 36 0 32 '
C. B C = 74 ( c m ) ; B ^ ≈ 35 0 33 '
D. B C = 75 ( c m ) ; B ^ ≈ 35 0 32 '
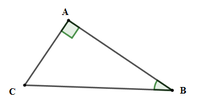
Xét tam giác ABC vuông tại A có:
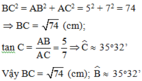
Đáp án cần chọn là: A
Đúng 1
Bình luận (0)
Cho tam giác giác abc , có ad là tia phân giác bac có ab=5cm ; ac=7cm; bd=2cm , tính CD
Xét ΔACB có AD là phân giác
nên BD/AB=CD/AC
=>CD/7=2/5
=>CD=2,8cm
Đúng 4
Bình luận (0)
Cho tam giác ABC vuông tại a a tính AC biết BC=13cm AB=5cm b tính BC biết AB=4cm AC=7cm
a, Áp dụng định lý Pitago:
`AB^2 + AC^2 = BC^2`
`=> 25 + AC^2 = 169`
`=> AC^2 = 144`
`=> sqrt 144 = 12`.
b. Áp dụng định lý Pytago ta có:
`AB^2 + AC^2 = BC^2`
`16 + 49 = BC^2`
`BC^2 = 65`
`BC = sqrt 65`.
Đúng 5
Bình luận (0)
Áp dụng định lí Pitago trong tam giác ABC vuông tại A
AC = BC2 + AB2
= 132 + 52
= \(\sqrt{194}\) = 14 cm
Áp dụng định lí Pitago trong tam giác ABC cân tại A
BC = AB2 + AC2
= 42 + 72
= \(\sqrt{65}\) = 8 cm
Đúng 1
Bình luận (0)
cho tam giác ABC biết AB = 7cm , Bc = 11cm, AC = 5cm . so sánh các cạnh
Cái này dễ mà bạn, người ta cho sẵn số đo rồi mà
AC< AB< BC
cho tam giác ABC với AB = 5cm, AC = 6cm, BC = 7cm. Gọi G là trọng tâm của tam giác ABC, O là giao điểm của 2 tia phân giác trong của tam giác ABC. Chứng minh rằng GO // AC
Bạn xem lời giải ở đường link sau nhé:
Câu hỏi của Thanh Thanh - Toán lớp 8 - Học toán với OnlineMath
Cho tam giác ABC có AB = 3cm, AC = 5cm, BC = 7cm; tam giác MNP ~ tam giác ABC và có chu vi bằng 75cm. Tính độ dài các cạnh của tam giác MNP
Cho tam giác ABC có
A
B
5
c
m
,
A
C
7
c
m
,
B
C
8
c
m
.
Khẳng định nào sau đây là đúng: A. ∠C ∠A ∠B B. ∠A ∠C ∠B C. ∠C ∠B ∠A D. ∠A ∠B ∠C
Đọc tiếp
Cho tam giác ABC có A B = 5 c m , A C = 7 c m , B C = 8 c m . Khẳng định nào sau đây là đúng:
A. ∠C < ∠A < ∠B
B. ∠A < ∠C < ∠B
C. ∠C < ∠B < ∠A
D. ∠A < ∠B < ∠C
Ta có: AB < AC < BC ⇒ C < B < A . Chọn C
Đúng 0
Bình luận (0)






