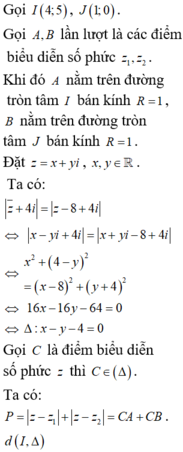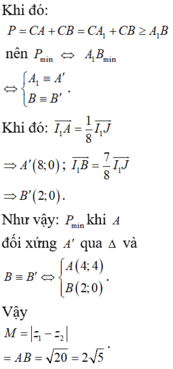Nếu |z|=1 thì (z2-1)/z =
H24
Những câu hỏi liên quan
Cho các số phức
z
,
z
1
,
z
2
thỏa mãn
z
1
-
4
-
5
i
z
2
-
1
1
,
...
Đọc tiếp
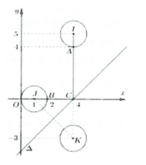
Cho các số phức z , z 1 , z 2 thỏa mãn z 1 - 4 - 5 i = z 2 - 1 = 1 , z ¯ + 4 i = z - 8 + 4 i . Tính M = z 1 - z 2 khi P = z - z 1 + z - z 2 đạt giá trị nhỏ nhất.
A. 41
B. 6
C. M = 2 5
D. 8
Cho phương trình trên tập họp số phức
z
2
+
a
x
+
b
0
. Nếu phương trình nhận số phức
z
1
+
i
làm một nghiệm thì a và b bằng. A. a -2, b 2 B. a 1, b 5 C. a 2, b -2 D. a 2, b -4
Đọc tiếp
Cho phương trình trên tập họp số phức z 2 + a x + b = 0 . Nếu phương trình nhận số phức z = 1 + i làm một nghiệm thì a và b bằng.
A. a = -2, b = 2
B. a = 1, b = 5
C. a = 2, b = -2
D. a = 2, b = -4
Cho số phức z có
z
1
. Tìm giá trị lớn nhất của biểu thức
P
z
2
-
z
+
z
2
+
z
+
1
. A.
13
4
...
Đọc tiếp
Cho số phức z có z = 1 . Tìm giá trị lớn nhất của biểu thức P = z 2 - z + z 2 + z + 1 .
A. 13 4
B. 3
C. 3
D. 11 4
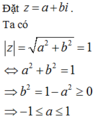
Theo bài ra ta có:
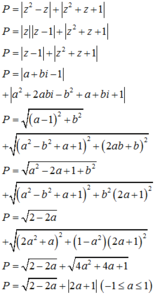
Sử dụng MTCT ta tìm được P m a x = 3 , 25 .
Chọn A.
Đúng 0
Bình luận (0)
Tìm giá trị lớn nhất của P = | z 2 - z| + | z 2 + z + 1| với z là số phức thỏa mãn |z| = 1
A. 3
B. 3
C. 13 4
D. 5
Đáp án C.
Với z = a + bi(a,b ∈ ℝ ), ta có:
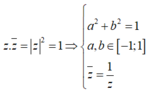
Do đó biến đổi ta được:
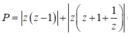
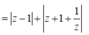
![]()
![]()
![]()
Khảo sát hàm ![]() trên đoạn [-1;1] ta được:
trên đoạn [-1;1] ta được:
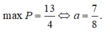
Đúng 0
Bình luận (0)
Cho 3 số phức
z
,
z
1
,
z
2
thỏa mãn
z
−
1
+
2
i
z
+
3
−
4
i
,
z
1...
Đọc tiếp
Cho 3 số phức z , z 1 , z 2 thỏa mãn z − 1 + 2 i = z + 3 − 4 i , z 1 + 5 − 2 i = 2 , z 2 − 1 − 6 i = 2. Tính giá trị nhỏ nhất của biểu thức T = z − z 1 + z − z 2 + 4
A. 2 3770 13
B. 10361 13
C. 3770 13
D. 10361 26
Cho các số phức z,
z
1
,
z
2
thỏa mãn
|
z
1
-
4
-
5
i
|
|
z
2
-
1
|
và
z
¯
+
4
i...
Đọc tiếp
Cho các số phức z, z 1 , z 2 thỏa mãn | z 1 - 4 - 5 i | = | z 2 - 1 | và z ¯ + 4 i = z - 8 + 4 i . Tính M = | z 1 - z 2 | khi P = | z - z 1 | + | z - z 2 | đạt giá trị nhỏ nhất.
![]()
![]()
![]()
![]()
Cho phương trình trên tập họp số phức
z
2
+
a
z
+
b
0
a
,
b
∈
ℝ
. Nếu phương trình nhận số phức
z
1
+
i
làm một nghiệm thì a và b bằng. A. a -2, b 2 B. a 1, b 5 C. a 2, b -2 D. a...
Đọc tiếp
Cho phương trình trên tập họp số phức z 2 + a z + b = 0 a , b ∈ ℝ . Nếu phương trình nhận số phức z = 1 + i làm một nghiệm thì a và b bằng.
A. a = -2, b = 2
B. a = 1, b = 5
C. a = 2, b = -2
D. a = 2, b = -4
Chọn A.
Phương pháp: Thế nghiệm vào phương trình và sử dụng định nghĩa về hai số phức bằng nhau.
Cách giải: Thay nghiệm z = 1+ i vào phương trình ta có:
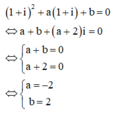
Đúng 0
Bình luận (0)
Cho số phức z thỏa |z| = 1. Tìm giá trị lớn nhất của P = | z 2 + z | + | z 2 - z |
A. 14/5.
B. 4.
C. 2 2 .
D. 2 3
nếu x;y;z là các số dương thì \(^{\frac{x2}{y+z}+\frac{y2}{x+z}+\frac{z2}{x+y}>=\frac{x+y+z}{2}}\)
Áp dụng bất đẳng thức Cauchy - Schwarz dưới dạng Engel ta có :
\(\frac{x^2}{y+z}+\frac{y^2}{x+z}+\frac{z^2}{x+y}\ge\frac{\left(x+y+z\right)^2}{y+z+x+z+x+y}=\frac{\left(x+y+z\right)^2}{2\left(x+y+z\right)}=\frac{x+y+z}{2}\)
Dấu "=" xảy ra <=> \(x=y=z=1\)
Vậy ............
Đúng 0
Bình luận (0)