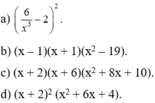(x2+8x+7)(x+3)(x+5)+15
TA
Những câu hỏi liên quan
Phân tích đa thức thành nhân tử bằng phương pháp đặt ẩn phụ:a)
36
x
6
−
24
x
3
+
4
;
b)
(
x
2
-
1
)
2
- 18(x + l)(x -1);c) (x + l)(x + 3)(x + 5)(x + 7...
Đọc tiếp
Phân tích đa thức thành nhân tử bằng phương pháp đặt ẩn phụ:
a) 36 x 6 − 24 x 3 + 4 ;
b) ( x 2 - 1 ) 2 - 18(x + l)(x -1);
c) (x + l)(x + 3)(x + 5)(x + 7) +15;
d) ( x 2 + x + 4 ) 2 + 8x( x 2 + x + 4) + 15 x 2 .
Phân tích thành nhân tử
2 + x )2 + 4x2 + 4x - 12
2 + 8x + 7)(x2 + 8x + 15) + 15
8x2 + 10x - 3
a: (x^2+x)^2+4x^2+4x-12
=(x^2+x)^2+4(x^2+x)-12
=(x^2+x+6)(x^2+x-2)
=(x^2+x+6)(x+2)(x-1)
b: =(x^2+8x)^2+22(x^2+8x)+105+15
=(x^2+8x)^2+22(x^2+8x)+120
=(x^2+8x+10)(x^2+8x+12)
=(x^2+8x+10)(x+2)(x+6)
c: =8x^2+12x-2x-3
=(2x+3)(4x-1)
Đúng 0
Bình luận (0)
Phân tích thành nhân tửa,(x2 + x )2 + 4x2 + 4x - 12b, (x2 + 8x + 7)(x2 + 8x + 15) + 15c,8x2 + 10x - 3
Đọc tiếp
Phân tích thành nhân tử
a,(x2 + x )2 + 4x2 + 4x - 12
b, (x2 + 8x + 7)(x2 + 8x + 15) + 15
c,8x2 + 10x - 3
a: =(x^2+x)^2+4(x^2+x)-12
=(x^2+x+6)(x^2+x-2)
=(x^2+x+6)(x+2)(x-1)
b: =(x^2+8x)^2+22(x^2+8x)+120
=(x^2+8x+12)(x^2+8x+10)
=(x+2)(x+6)(x^2+8x+10)
c: =8x^2+12x-2x-3
=(2x+3)(4x-1)
Đúng 0
Bình luận (0)
Kết quả của phép tính (x − 5)(x + 3) là:
A. x 2 − 15
B. x 2 − 8x − 15
C. x 2 + 2x − 15
D. x 2 − 2x − 15
Chọn D.
(x − 5)(x + 3) = x(x + 3) – 5( x + 3) = x 2 + 3x - 5x - 15 = x 2 − 2x − 15
Đúng 0
Bình luận (0)
Chứng minh đa thức f(x)=9x+1(x+3)(x+5)(x+7)+15f(x)=9x+1(x+3)(x+5)(x+7)+15 chia hết cho đa thức g(x)=x2+8x+10
(x2+x)2 -14 (x2-x)+24
(x2+x)2+4x2+4x-12
x4+2x3+5x2+4x-12
(x+1)(x+2)(x+3)(x+4)+1
(x+1)(x+3)(x+5)(x+7)+15
(x+1)(x+2)(x+3)(x+4)-24
(x2+4x+8)2+3x(x2+4x+8)+2x3
(x2+x+1)(x2+x+2)-12
(x2+8x+7)(x2+8x+15)+15
(x+2)(x+3)(x+4)(x+5)-24
Bài 4. Tìm số nguyên x, biết: a) (x2 −9)(5x+15) 0 b) x2 – 8x 0c) 5+12.(x−1)2 53 d) (x− 5)2 36e) (3x+−5)3 64 f) 42x + 24x+3 144
Đọc tiếp
Bài 4. Tìm số nguyên x, biết:
a) (x2 −9)(5x+15) =0 |
|
| b) x2 – 8x= 0 |
c) 5+12.(x−1)2 = 53 |
|
| d) (x− 5)2 = 36 |
e) (3x+−5)3 = 64 |
|
| f) 42x + 24x+3 = 144 |
Lời giải:
a. $(x^2-9)(5x+15)=0$
$\Rightarrow x^2-9=0$ hoặc $5x+15=0$
Nếu $x^2-9=0$
$\Rightarrow x^2=9=3^2=(-3)^2$
$\Rightarrow x=3$ hoặc $-3$
Nếu $5x+15=0$
$\Rightarrow x=-3$
b.
$x^2-8x=0$
$\Rightarrow x(x-8)=0$
$\Rightarrow x=0$ hoặc $x-8=0$
$\Rightarrow x=0$ hoặc $x=8$
c.
$5+12(x-1)^2=53$
$12(x-1)^2=53-5=48$
$(x-1)^2=48:12=4=2^2=(-2)^2$
$\Rightarrow x-1=2$ hoặc $x-2=-2$
$\Rightarrow x=3$ hoặc $x=0$
d.
$(x-5)^2=36=6^2=(-6)^2$
$\Rightarrow x-5=6$ hoặc $x-5=-6$
$\Rightarrow x=11$ hoặc $x=-1$
e.
$(3x-5)^3=64=4^3$
$\Rightarrow 3x-5=4$
$\Rightarrow 3x=9$
$\Rightarrow x=3$
f.
$4^{2x}+2^{4x+3}=144$
$2^{4x}+2^{4x}.8=144$
$2^{4x}(1+8)=144$
$2^{4x}.9=144$
$2^{4x}=144:9=16=2^4$
$\Rightarrow 4x=4\Rightarrow x=1$
Đúng 2
Bình luận (0)
Tìm x:
a) x(x+1)(x+2)(x+3) = (x2+3x+1)2+x
b) (x+1)(x+3)(x+5)(x+7) = (x2+8x+11)2+2x
c) (x2-x+1)(x2+x+1)(x-1)(x+1)=63
a) \(x\left(x+1\right)\left(x+2\right)\left(x+3\right)=\left(x^2+3x+1\right)^2+x\)
\(\Leftrightarrow\left(x^2+3x\right)\left(x^2+3x+2\right)=\left(x^2+3x+1\right)^2+x\)
\(\Leftrightarrow\left(t-1\right)\left(t+1\right)=t^2+x\) (với \(t=x^2+3x+1\))
\(\Leftrightarrow t^2-1=t^2+x\)
\(\Leftrightarrow x=-1\).
b) \(\left(x+1\right)\left(x+3\right)\left(x+5\right)\left(x+7\right)=\left(x^2+8x+11\right)^2+2x\)
\(\Leftrightarrow\left(x^2+8x+7\right)\left(x^2+8x+15\right)=\left(x^2+8x+11\right)^2+2x\)
\(\Leftrightarrow\left(t-4\right)\left(t+4\right)=t^2+2x\) (với \(t=x^2+8x+11\))
\(\Leftrightarrow t^2-16=t^2+2x\)
\(\Leftrightarrow x=-8\)
c) \(\left(x^2-x+1\right)\left(x^2+x+1\right)\left(x-1\right)\left(x+1\right)=63\)
\(\Leftrightarrow\left(x^3-1\right)\left(x^3+1\right)=63\)
\(\Leftrightarrow x^6-1=63\)
\(\Leftrightarrow x^6=64\)
\(\Leftrightarrow x=\pm2\)
Đúng 4
Bình luận (0)
https://onlinemath.vn/cau-hoi/viet-1-doan-van-tong-phan-hop-khoang-12-cau-phan-tich-kho-tho-thu-2-bai-que-huong-trong-do-su-dung-1-cau-cam-than-vs-cau-ghep-chi-ro.8109170456376 help
Đúng 0
Bình luận (0)
a) x2(x - 5) + 5 - x = 0; b) 3x4 - 9x3 = -9x2 + 27x;
c) x2(x + 8) + x2 = -8x; d) (x + 3)(x2 -3x + 5) = x2 + 3x.
e) 3x(x - 1) + x - 1 = 0;
f) (x - 2)(x2 + 2x + 7) + 2(x2 - 4) - 5(x - 2) = 0;
g) (2x - 1)2 - 25 = 0;
h) x3 + 27 + (x + 3)(x - 9) = 0.
i)8x3 - 50x = 0; k) 2(x + 3)-x2 - 3x = 0;
m)6x2 - 15x - (2x - 5)(2x + 5) =
a: \(\Leftrightarrow\left(x-5\right)\left(x+1\right)\left(x-1\right)=0\)
\(\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-1\\x=1\end{matrix}\right.\)
d: \(\Leftrightarrow\left(x+3\right)\left(x^2-4x+5\right)=0\)
\(\Leftrightarrow x+3=0\)
hay x=-3
Đúng 0
Bình luận (0)
Phân tích các đa thức thành phân tử :
(x2+x)2 -14 (x2-x)+24
(x2+x)2+4x2+4x-12
x4+2x3+5x2+4x-12
(x+1)(x+2)(x+3)(x+4)+1
(x+1)(x+3)(x+5)(x+7)+15
(x+1)(x+2)(x+3)(x+4)-24
(x2+4x+8)2+3x(x2+4x+8)+2x3
(x2+x+1)(x2+x+2)-12
(x2+8x+7)(x2+8x+15)+15
(x+2)(x+3)(x+4)(x+5)-24
Đọc tiếp
Phân tích các đa thức thành phân tử :
(x2+x)2 -14 (x2-x)+24
(x2+x)2+4x2+4x-12
x4+2x3+5x2+4x-12
(x+1)(x+2)(x+3)(x+4)+1
(x+1)(x+3)(x+5)(x+7)+15
(x+1)(x+2)(x+3)(x+4)-24
(x2+4x+8)2+3x(x2+4x+8)+2x3
(x2+x+1)(x2+x+2)-12
(x2+8x+7)(x2+8x+15)+15
(x+2)(x+3)(x+4)(x+5)-24