cho hình bình hành ABCD. Đường tròn (O;R)đi qua 2 điểm A và B, đường tròn (I;K) đi qua Bvà C. Gỉa sử 2 đường tròn O và I cát nhau tại điểm thứ hai là M . cm bán kính đường tròn ngoại tiếp tam giác ADM cũng bằng R.
giài giúp em câu này với ạ
Cho đường tròn tâm O bán kính R và 2 điểm phân biệt C, D nằm ngoài đường tròn . Hãy dựng dây cung AB của đường tròn sao cho ABCD là hình bình hành
Cho hình bình hành ABCD. Đường tròn (O;R) đi qua A và B, đường tròn (I;R) đi qua B và C.(O) và (I) cắt nhau tại điểm thứ 2 là M. CMR: bán kính đường tròn ngoại tiếp tam giác ADM bằng R.
Cho hình bình hành ABCD tâm O. Gọi (I), (J) là đường tròn ngoại tiếp tam giác AOB, COD.
Chứng minh rằng (I),(J) tiếp xúc ngoài với nhau
cho hình bình hành ABCD tâm O.Gọi H,I,V lần lượt là hình chiếu của A lên BD,BC,CD.Chứng minh O,H,I,V thuộc một đường tròn
Cho hbh ABCD. Gọi O là tâm đường tròn nội tiếp tam giác ABC
Biết khoảng cách từ O đến A và 2 đường thẳng AD và AC tương ứng là 5,4,3
tính diện tích hình bình hành ABCD
Bài này bạn chia làm 2 trường hợp Q thuộc đoạn AD và Q nằm ngoài AD
Trường hợp 1Từ gt => OA=5, OQ=4, và OM=ON=OP=3
Áp dụng định lý Pytago cho các tam giác QAO và tam giác MAO vuông ứng ứng lần lượt tại Q và M ta có:
AQ2=AO2-OQ2=52-42=32 => AQ+3
AM2=AO2-OM2=52-32=42 => AM=4
=> AM=QO và AQ=MO => AMOQ là hình bình hành
Mà \(\widehat{AMO}=90^o\) => AMOQ là hình chữ nhật
=> \(\widehat{QAM}=90^o\)
Từ đó ta có ABCD là hình chữ nhật
Đặt CP=CN=x
Áp dụng định lý Pytago cho tam giác ABC vuông tại B, với BM=ON=3
AP=AM=4; AB=AM+BM=7
ta có: CA2=AB2+BC2 <=> (x+4)2=72+(x+3)2
=> x=21 và BC=24
Vậy diện tích hình bình hành ABCD là 7.24=168 (đv diện tích)
Cmtt trường hợp 1 ta tính được
\(\widehat{ACB}=90^o;AC=7;BC=24\)
Từ đó ta tính được
SABCD=168 (đv diện tích)
Cho hình bình hành ABCD có đỉnh D thuộc đường tròn (O) đường kính AB. Gọi N là giao điểm của AC với (O). Kẻ DM vuông góc AC tại M.
a) Chứng minh BCDM nội tiếp đường tròn. Xác định tâm I của đường tròn này
b) Chứng minh DB.DC = DN.AC
c) Xác định vị trí điểm D để tứ giác BIDO là hình vuông
a: góc DMC=góc DBC=90 độ
=>DMBC nội tiếp đường tròn đường kính dC
I là trung điểm của DC
b: góc ANB=1/2*180=90 độ
=>ΔANB vuông tại N
=>góc NAB+góc NBA=90 độ và DM//BN
Gọi K là giao của AC và BD
=>K là trung điểm chung của AC và BD
Xét ΔKDM vuông tại M và ΔKBN vuông tại N có
KD=KB
góc DKM=góc BKN
=>ΔKDM=ΔKBN
=>DM=BN
mà DM//BN
nên DMBN là hình bình hành
=>góc MBD=góc BDN=góc MCD
Xét ΔDAC và ΔNBD có
góc DCA=góc NDB
góc DAC=góc NBD
=>ΔDAC đồng dạng với ΔNBD
=>DC/DN=AC/BD
=>DC*DB=DN*CA
Cho hình thang ABCD đáy lớn AD đáy nhỏ BC nội tiếp đường tròn tâm O. AB và CD kéo dài cắt nhau tại I. Các tiếp tuyến của đường tròn (O) tại B và D cắt nhau tại K.
a> C/m tứ giác BIKD nội tiếp
b> C/m IK//BC
c> Hình thang ABCD cần thêm điều kiện gì để tứ giác AIKD là hình bình hành. Khi đó c/m hệ thức: IC.IE=ID.CE( với E là giao điểm của BK và ID)
d> Vẽ hình bình hành BDKM, đường tròn ngoại tiếp tam giác BKM cắt đường tròn (O) tại điểm thứ 2N.C/m 3 điểm D,M,N thẳng hàng.
Cho em xin đáp án câu c bài này ah
Cho hình bình hành ABCD, 2 đường chéo cắt nhau tại O. Vẽ đường tròn tâm O bất kì cắt AB, BC, CD, DA lần lượt tại M, N, P, Q. Xác định dạng của MNPQ
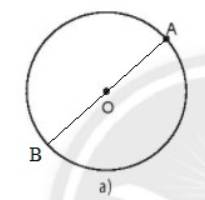
a) Lấy một điểm A bất kì trên đường tròn tâm O. Hãy tìm điểm B trên đường tròn sao cho O là trung điểm của đoạn thẳng AB (Hình 1a).
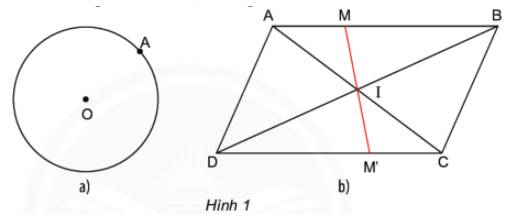
b) Cho hình bình hành ABCD, hai đường chéo AC và BD cắt nhau tại I. Đường thẳng qua I cắt AB tại M và cắt CD tại M. Đo rồi so sánh độ dài IM và IM (Hình 1b).
a) O là trung điểm của AB, Khi đó AB là đường kính của đường tròn.
b) Độ dài IM = IM'.
Cho tam giác ABC cân tại A, nội tiếp đường tròn tâm O. Vẽ hình bình hành ABCD. Tiếp tuyến tại C của đường tròn cắt đường thẳng AD tại N. Chứng minh:
a, Đường thẳng AD là tiếp tuyến của (O)
b, Ba đường thẳng AC, BD và ON đồng quy
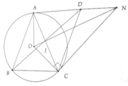
a, Tam giác ABC cân tại A nội tiếp (O)
=> OA ⊥ BC
=> OA ⊥ AD (vì AD//BC)
=> AD là tiếp tuyến của (O)
b, Chứng minh được ON là tia phân giác của A O D ^ mà ∆OAC cân tại O nên ON cũng là đường trung tuyến => ON cắt AC tại trung điểm I của AC => ON,AC,BD cùng đi qua trung điểm I của AC