GIÚP MÌNH CÂU CHỨNG MINH TỨ GIÁC MIHK NỘI TIẾP VỚI🥺
NL
Những câu hỏi liên quan
Câu 1: cho tam giác ABC (ba góc đều nhọn), các đường cao BD và CE.
a, Chứng minh tứ giác BEDC là tứ giác nội tiếp
b, Chứng minh AD.AC=AE.AB
Câu 2: cho tam giác đều ABC nội tiếp (O;6cm). Tính diện tích hình viên phân giới hạn bởi dây BC và cung nhỏ BC.
m.m giúp mình với ạ! mai phải nộp r :(
Câu 1: cho tam giác ABC (ba góc đều nhọn), các đường cao BD và CE.
a, Chứng minh tứ giác BEDC là tứ giác nội tiếp
b, Chứng minh AD.AC=AE.AB
Câu 2: cho tam giác đều ABC nội tiếp (O;6cm). Tính diện tích hình viên phân giới hạn bởi dây BC và cung nhỏ BC.
m.m giúp mình với ạ! mai phải nộp r :(
cho tam giác ABC nội tiếp đường tròn tâm O bán kính bằng 5cm, hai đường cao BM và CN cắt nhau tại H.
a, Chứng minh tứ giác AMHN nội tiếp
b, chứng minh tứ giác BNMC nội tiếp
c, chứng minh OA vuông góc với MN
Mọi người giải chi tiết giúp mình với nhé !! Cảm Ơn
A) góc amh=anh=90=>tứ giác amhn noi tiếp
B)Góc BMC = BNC =90->tứ giác BNMC nội tiếp
C)Gọi giao điểm của AO với MN là P. Kẻ đường kính AA'
Chứng minh ABC đồng dạng AMN
Chứng minh tứ giác PA'CM nội tiếp
Mà góc MCA'=90=>MPA'=90
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn nội tiếp (O), có AB<AC. Vẽ các đường cao BE, CF cắt nhau tại H
a. Chứng minh tứ giác BFEC nội tiếp
b. Chứng minh IE.IB=IF.IC
c. AO vuông góc với EF
(Giúp mình vẽ hình và giải bài với ạ, mình xin cảm ơn)
a: góc BFC=góc BEC=90 độ
=>BFEC nội tiếp
b: Sửa đề; HE*HB=HF*HC
Xét ΔHFB vuông tại F và ΔHEC vuông tại E có
góc FHB=góc EHC
=>ΔHFB đồng dạng với ΔHEC
=>HF/HE=HB/HC
=>HE*HB=HF*HC
c: Kẻ tiếp tuyến Ax của (O)
=>góc xAC=góc ABC=góc AEF
=>Ax//FE
=>FE vuông góc AO
Đúng 0
Bình luận (0)
giải giúp mình bài này với mình đang cần gấp
Cho tam giác ABC có ba góc nhọn nội tiếp (O,R). Hai đường cao AN và BM của tam giác ABC cắt nhau tại I
a Chứng minh tứ giác IMCN nội tiếp được một đường tròn
b chứng minh IA.IN=IM.IB
c tia BM cắt (O) tại H Chứng minh AI=AH
Giải thích các bước giải:
a) ΔABCΔABC có đường cao AN,BMAN,BM
⇒AN⊥BC;BM⊥AC⇒AN⊥BC;BM⊥AC
Xét tứ giác IMCNIMCN có:
ˆIMC=ˆINC=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)IMC^=INC^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
⇒ˆIMC+ˆINC=1800⇒IMC^+INC^=1800
⇒⇒ tứ giác IMCNIMCN nội tiếp
b) Xét ΔBINΔBIN và ΔAIMΔAIM có:
ˆBNI=ˆAMI=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)BNI^=AMI^=900(AN⊥BC;BM⊥AC;I∈AN;I∈BM)
ˆBIN=ˆAIMBIN^=AIM^ (đối đỉnh)
⇒⇒ ΔBIN∽ΔAIMΔBIN∽ΔAIM (g.g)
⇒IBIA=INIM⇒IA.IN=IM.IB⇒IBIA=INIM⇒IA.IN=IM.IB
c) Tứ giác IMCNIMCN nội tiếp
⇒ˆAIH=ˆNCM⇒AIH^=NCM^ hay ˆAIH=ˆACBAIH^=ACB^
Xét (O)(O) có: ˆACB=ˆAHBACB^=AHB^ (2 góc nội tiếp cùng chắn cung ABAB)
⇒ˆAIH=ˆAHB⇒AIH^=AHB^
⇒ˆAIH=ˆAHI⇒ΔAIH⇒AIH^=AHI^⇒ΔAIH cân tại A⇒AI=AH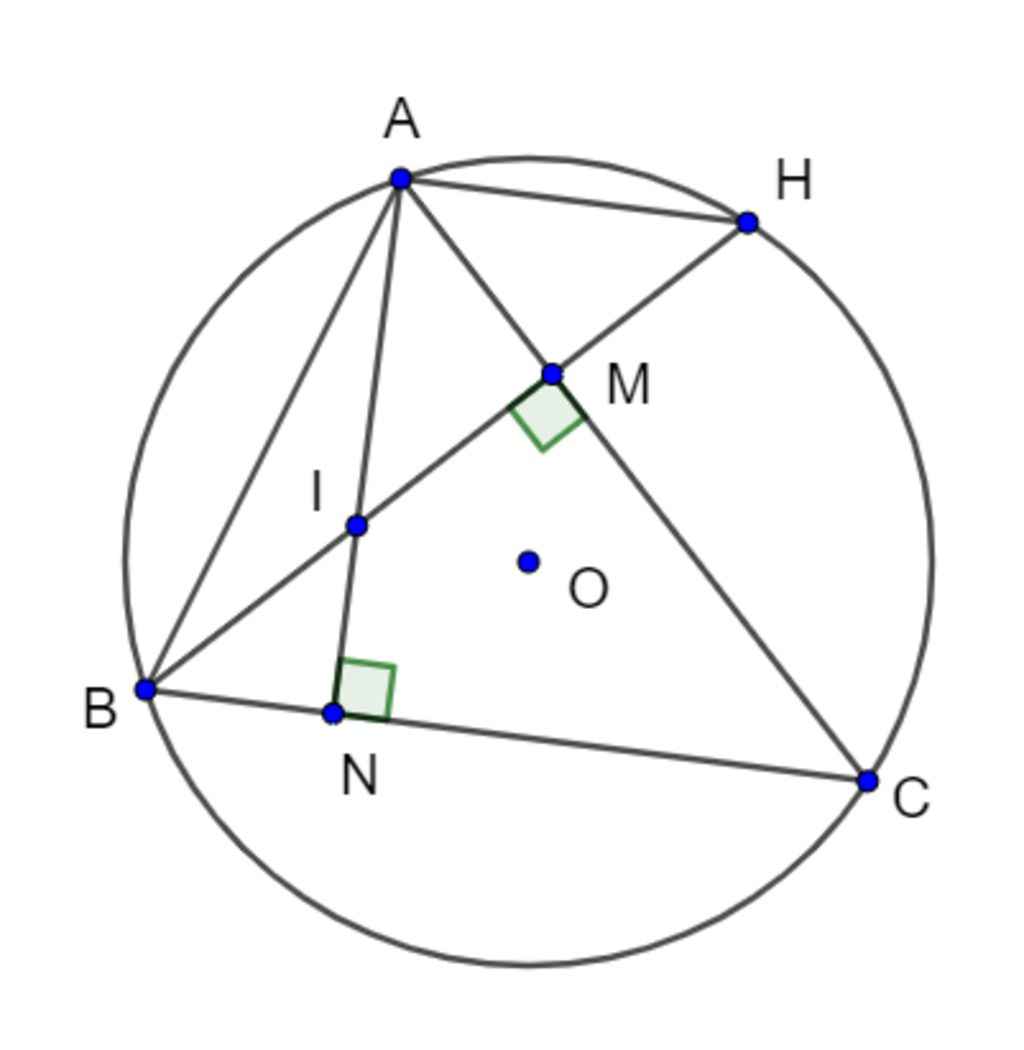
Đúng 0
Bình luận (0)
Giải giúp mình câu b ạ
Cho tam giác ABC nhọn nội tiếp đường tròn (O), các đường cao AD, BE, CF cắt nhau tại H. a) Chứng minh tứ giác BFHD nội tiếp đường tròn và CFD = CFE b) Gọi M là giao điểm của CB và EF. Từ B kẻ đường thắng song song với AC, đường thắng này cắt AM và AH lần lượt tại I và K. Chứng minh BI = BK.
Cho tam giác ABC(AB<AC) vẽ hai đường cao IC và BD gọi h là giao điểm của IC và BD ah cắt BC tại I a )chứng minh tứ giác bcde là tứ giác nội tiếp. b )chứng minh ae nhân ab = ad nhân AC. c)chứng minh EC là tia phân giác của góc ied( giúp mình câu c)
a: góc BEC=góc BDC=90 độ
=>BEDC nội tiêp
b: Xet ΔAEC vuông tại E và ΔADB vuông tại D có
góc EAC chung
=>ΔAEC đồng dạng với ΔADB
=>AE/AD=AC/AB
=>AE*AB=AD*AC
c: góc DEH=goc IAC
góc IEC=góc DBC
góc IAC=góc DBC
=>góc DEH=góc IEC
=>EH là phân giác của góc DEI
Đúng 1
Bình luận (0)
Có ai giúp mình chứng minh bài toán hình này với:
CM Tâm đường tròn nội tiếp 1 tứ giác ngoại tiếp và giao điểm 2 đường chéo của tứ giác đó thẳng hàng.
mình cũng chịu bởi vì năm nay minh học lớp 6 thôi
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
Cho tứ giác ABCD nội tiếp nửa đưởng tròn đường kính AD. Hai đường chéo AC và BD cắt nhau tại E. Vẽ EF vuông góc vớI AD. Chứng minh:
a, Tứ giác ABEF, DCEF nội tiếp
b, CA là phân giác của góc BCF
c, Gọi M là trung điểm của DE, chứng minh tứ giác BCMF nội tiếp.
MỌI NGƯỜI AI BIẾT LÀM GIẢI GIÚP MÌNH PHẦN C. CẢM ƠN NHIỀU <3