Hãy so sánh động năng của hai vật trước khi chạm chân dốc
HN
Những câu hỏi liên quan
Trong môn trượt tuyết, một vận động viên sau khi trượt trên đoạn đường dốc thì trượt ra khỏi dốc theo phương ngang ở độ cao 90 m so với mặt đất. Người đó bay xa được 180 m trước khi chạm đất. Hỏi tốc độ của vận động viên đó ngay trước khi chạm đất là bao nhiêu ? Lấy
g
10
m
/
s
2
. A. 45 m/s. B. 60 m/s. C. 42 m/s. D. 90 m/s.
Đọc tiếp
Trong môn trượt tuyết, một vận động viên sau khi trượt trên đoạn đường dốc thì trượt ra khỏi dốc theo phương ngang ở độ cao 90 m so với mặt đất. Người đó bay xa được 180 m trước khi chạm đất. Hỏi tốc độ của vận động viên đó ngay trước khi chạm đất là bao nhiêu ? Lấy g = 10 m / s 2 .
A. 45 m/s.
B. 60 m/s.
C. 42 m/s.
D. 90 m/s.
Chọn B.
Tầm bay xa của vận động viên là
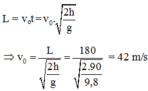
Phương trình vận tốc
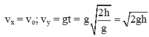
Tốc độ của vận động viên ngay trước khi chạm đất là
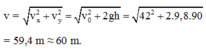
Đúng 0
Bình luận (0)
Trong môn trượt tuyết, một vận động viên sau khi trượt trên đoạn đường dốc thì trượt ra khỏi dốc theo phương ngang ở độ cao 90m so với mặt đất. Người đó bay xa được 180m trước khi chạm đất. Hỏi tốc độ của vận động viên đó ngay trước khi chạm đất là bao nhiêu ? Lấy g 9,8m/s2. A. 45m/s B. 60m/s C. 42m/s D. 90m/s
Đọc tiếp
Trong môn trượt tuyết, một vận động viên sau khi trượt trên đoạn đường dốc thì trượt ra khỏi dốc theo phương ngang ở độ cao 90m so với mặt đất. Người đó bay xa được 180m trước khi chạm đất. Hỏi tốc độ của vận động viên đó ngay trước khi chạm đất là bao nhiêu ? Lấy g = 9,8m/s2.
A. 45m/s
B. 60m/s
C. 42m/s
D. 90m/s
Chọn đáp án B
Tầm bay xa của vận động viên là :
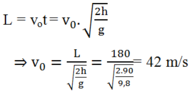
Phương trình vận tốc vx = vo
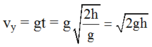
Tốc độ của vận động viên ngay trước khi chạm đất là
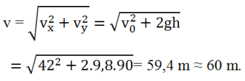
Đúng 0
Bình luận (0)
Trong môn trượt tuyết, một vận động viên sau khi trượt trên đoạn đường dốc thì trượt ra khỏi dốc theo phương ngang ở độ cao 90 m so với mặt đất. Người đó bay xa được 180 m trước khi chạm đất. Hỏi tốc độ của vận động viên đó ngay trước khi chạm đất là bao nhiêu ? Lấy g 9,8
m
/
s
2
. A. 45 m/s B. 60 m/s C. 42 m/s D. 90 m/s.
Đọc tiếp
Trong môn trượt tuyết, một vận động viên sau khi trượt trên đoạn đường dốc thì trượt ra khỏi dốc theo phương ngang ở độ cao 90 m so với mặt đất. Người đó bay xa được 180 m trước khi chạm đất. Hỏi tốc độ của vận động viên đó ngay trước khi chạm đất là bao nhiêu ? Lấy g = 9,8 m / s 2 .
A. 45 m/s
B. 60 m/s
C. 42 m/s
D. 90 m/s.
Trong môn trượt tuyết, một vận động viên sau khi trượt trên đoạn đường dốc thì trượt ra khỏi dốc theo phương ngang ở độ cao 90 m so với mặt đất. Người đó bay xa được 180 m trước khi chạm đất. Hỏi tốc độ của vận động viên đó ngay trước khi chạm đất là bao nhiêu ? Lấy g = 9,8 m/ s 2
A. 45 m/s.
B. 60 m/s.
C. 42 m/s.
D. 90 m/s.
Trong môn trượt tuyết, một vận động viên sau khi trượt trên đoạn đường dốc thì trượt ra khỏi dốc theo phương ngang ở độ cao 90 m so với mặt đất. Người đó bay xa được 180 m trước khi chạm đất. Hỏi tốc độ của vận động viên đó ngay trước khi chạm đất là bao nhiêu ? Lấy g = 9,8 m/ s 2 .
A. 45 m/s
B. 60 m/s
C. 42 m/s.
D. 90 m/s.
Chọn B
Tầm bay xa của vận động viên là:
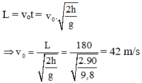
Phương trình vận tốc
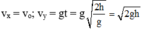
Tốc độ của vận động viên ngay trước khi chạm đất là
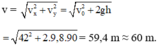
Đúng 0
Bình luận (0)
Từ độ cao 10m, thả vật có khối lượng 2kg, lấy g = 10m/s2.
A. Tìm động năng, thế năng, và cơ năng của vật ?
B. Tìm độ cao cực đại mà vật đạt được so với mặt đất ?
C. Xác định vận tốc của vật khi Wđ = Wt ?
D. Xác định vận tốc của vật trước khi chạm đất ?
A. Động năng của vật:
\(W_đ=\dfrac{1}{2}.m.\upsilon^2=\dfrac{1}{2}.2.0^2=0J\)
Thế năng của vật:
\(W_t=m.g.z=2.10.10=200J\)
Cơ năng của vật:
\(W=W_đ+W_t=0+200=200J\)
B. Bảo toàn cơ năng thì ta có:
\(W_t=W_t'\)
\(\Leftrightarrow W_t=m.g.z_{max}\)
\(\Leftrightarrow z_{max}=\dfrac{W_t}{m.g}\)
\(\Leftrightarrow z_{max}=\dfrac{200}{2.10}\)
\(\Leftrightarrow z_{max}=10m\)
C. Ta có: \(W_t=W_đ\)
Bảo toàn cơ năng:
\(W=W_2\)
\(\Leftrightarrow W=W_t+W_đ\)
\(\Leftrightarrow W=2W_đ\)
\(\Leftrightarrow W=2\left(\dfrac{1}{2}m.\upsilon^2\right)\)
\(\Leftrightarrow\upsilon^2=\dfrac{W}{m}\)
\(\Leftrightarrow\upsilon^2=\dfrac{200}{2}=100\)
\(\Leftrightarrow\upsilon=\sqrt{100}=10m/s\)
Đúng 2
Bình luận (0)
Làm thế nào để xác định được lực tương tác giữa hai vật khi va chạm nếu không biết được động lượng của các vật trước và sau tương tác. Trong quá trình va chạm (Hình 19.1), động lượng và động năng của hệ có được bảo toàn hay không? Ngoài ra, những kiến thức về động lượng có thể được vận dụng trong thực tiễn như thế nào?
Đọc tiếp
Làm thế nào để xác định được lực tương tác giữa hai vật khi va chạm nếu không biết được động lượng của các vật trước và sau tương tác. Trong quá trình va chạm (Hình 19.1), động lượng và động năng của hệ có được bảo toàn hay không? Ngoài ra, những kiến thức về động lượng có thể được vận dụng trong thực tiễn như thế nào?

- Trong quá trình va chạm động lượng và động năng của hệ có được bảo toàn.
- Ngoài ra, những kiến thức về động lượng có thể được vận dụng trong thực tiễn như:
+ Hệ thống túi khí và đai an toàn trong ô tô giúp người ngồi trong xe hạn chế tối đa chấn thương khi xảy ra va chạm giao thông.
+ Vận động viên nhảy xa nhún chân, chùng đầu gối khi tiếp đất mục đích để tăng thời gian va chạm, giảm lực tác dụng.
+ Chế tạo hệ thống động cơ chuyển động bằng phản lực.
…
Đúng 0
Bình luận (0)
Một vật nặng 1200g được thả rơi xuống đất từ độ cao 100m. g= 10m/s2). Hãy tính:
a) Cơ năng lúc đầu? và vận tốc trước khi chạm đất.
b) Vận tốc khi động năng bằng thế năng?
c) Vận tốc khi vật ở độ cao 30m?
a)Cơ năng ban đầu:
\(W=\dfrac{1}{2}mv^2+mgz=\dfrac{1}{2}\cdot1,2\cdot0^2+1,2\cdot10\cdot100=1200J\)
Vận tốc khi chạm đất:
\(v=\sqrt{2gh}=\sqrt{2\cdot10\cdot100}=20\sqrt{5}\)m/s
b)Cơ năng tại nơi \(W_đ=W_t\):
\(W_2=2W_đ=2\cdot\dfrac{1}{2}mv'^2\)
Bảo toàn cơ năng: \(W=W_2\)
\(\Rightarrow1200=2\cdot\dfrac{1}{2}mv'^2\Rightarrow v'=10\sqrt{10}\)m/s
c)Cơ năng tại nơi \(h=30m\):
\(W_3=\dfrac{1}{2}mv^2+mgh=\dfrac{1}{2}\cdot1,2\cdot v^2+1,2\cdot10\cdot30=0,6v^2+360J\)
Bảo toàn cơ năng: \(W=W_3\)
\(\Rightarrow1200=0,6v^2+360\Rightarrow v=10\sqrt{14}\)m/s
Đúng 4
Bình luận (0)
Một vật có khối lượng 900g được đặt trên một đỉnh dốc dài 75cm và cao 45cm. Cho trượt không vật tốc ban đầu từ đỉnh dốc. Lấy
g
10
(
m
/
s
2
)
1. Sử dụng định luật bảo toàn cơ năng tìm:a. Xác định vận tốc của vật ở cuối chân dốc ?b. Xác định vị trí để
W
d
2
W
t...
Đọc tiếp
Một vật có khối lượng 900g được đặt trên một đỉnh dốc dài 75cm và cao 45cm. Cho trượt không vật tốc ban đầu từ đỉnh dốc. Lấy g = 10 ( m / s 2 )
1. Sử dụng định luật bảo toàn cơ năng tìm:
a. Xác định vận tốc của vật ở cuối chân dốc ?
b. Xác định vị trí để W d = 2 W t và vận tốc của vật khi đó. Tính thế năng cua vật ?
2. Sử dụng định lý động năng tìm:
a. Xác định vận tốc của vật của vật tại vị trí cách chân dốc 27cm.
b. Xác định quãng đường của vật khi vật đạt được vận tốc 1,2 m/s
1. Goi A là đỉnh dốc, B là chân dốc
Chọn mốc thế năng nằm tại chân dốc
a. Theo định luật bảo toàn cơ năng
W A = W B ⇒ m g z A = 1 2 m v B 2 ⇒ v B = 2 g z A = 2.10.0.45 = 3 ( m / s )
b. Gọi C là vị trí W d = 2 W t . Theo định luật bảo toàn cơ năng
W A = W C ⇒ m g z A = W d C + W t C = 3 W t C = 3 m g z C ⇒ z C = z A 3 = 0 , 45 3 = 0 , 15 ( m )
Theo bài ra
W d = 2 W t ⇒ 1 2 m v C 2 = 2 m g z C ⇒ v C = 4. g z C = 4.10.0 , 15 = 6 ( m / s )
Thế năng của vật tại C
W t C = m g z C = 0 , 9.10.0 , 15 = 1 , 35 ( J )
2. a. Quãng dường chuyển động của vật
s = 75 − 27 = 48 ( c m ) = 0 , 48 ( m )
Theo định lý động năng ta có
A = W d 2 − W d 1 ⇒ P x . s = 1 2 m v 2 2 ⇒ m g . sin α = 1 2 m v 2 2 ⇒ v 2 = 2 g . sin α . s
Mà sin α = 45 75 => v 2 = 2.10. 45 75 .0 , 48 = 2 , 4 ( m / s )
b. Theo định lý động năng
A / = W d 3 − W d 1 ⇒ P x s / = 1 2 m v 3 2 ⇒ P sin α . s / = 1 2 m v 3 2 ⇒ g . sin α . s / = 1 2 v 3 2 ⇒ s / = v 3 2 2. g . sin α = 1 , 2 2.10. 45 75 = 0 , 1 ( m )
Vậy vật đi được quãng đường 10cm
Đúng 0
Bình luận (0)




