Tính đạo hàm của hàm số y = x8 tại x=1
Cảm mơn mn rất nhìu ạ T^T
Cho hàm số \(y = {x^{22}}\)
a) Tính đạo hàm của hàm số trên tại điểm x bất kì
b) Tính đạo hàm của hàm số trên tại điểm \({x_0} = - 1\)
a) Ta có: \(f'\left( x \right) = \left( {{x^{22}}} \right)' = 22.{x^{21}}\)
b) Đạo hàm của hàm số tại điểm \({x_0} = - 1\) là: \(f'\left( { - 1} \right) = 22.{\left( { - 1} \right)^{21}} = - 22\)
Dùng định nghĩa tính đạo hàm của hàm số y = x 3 tại điểm x tùy ý.
Dự đoán đạo hàm của hàm số y = x 100 tại điểm x.
- Giả sử Δx là số gia của đối số tại xo bất kỳ. Ta có:
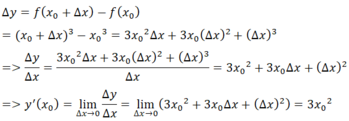
- Dự đoán đạo hàm của y = x100 tại điểm x là 100x99
a) Tính đạo hàm của hàm số \(y = {x^2}\) tại điểm \({x_0}\) bất kì bằng định nghĩa
b) Dự đoán đạo hàm của hàm số \(y = {x^n}\) tại điểm x bất kì
a)
\(\begin{array}{l}f'({x_0}) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f(x) - f({x_0})}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^2} - x_0^2}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{e^{2.\ln x}} - {e^{2.\ln {x_0}}}}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{e^{2.\ln {x_0}}}.\left( {{e^{2\ln x - 2\ln {x_0}}} - 1} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{x_0^2\left( {{e^{2.\ln x - 2\ln {x_0}}} - 1} \right)}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{x_0^2\left( {2\ln x - 2\ln {x_0}} \right)}}{{x - {x_0}}} = 2x_0^2\mathop {\lim }\limits_{x \to {x_0}} \frac{{\ln \left( {\frac{x}{{{x_0}}}} \right)}}{{x - {x_0}}} = 2x_0^2\mathop {\lim }\limits_{x \to {x_0}} \frac{{\ln \left( {1 + \frac{x}{{{x_0}}} - 1} \right)}}{{x - {x_0}}} = 2x_0^2\mathop {\lim }\limits_{x \to {x_0}} \frac{{\frac{x}{{{x_0}}} - 1}}{{x - {x_0}}} = 2x_0^2\mathop {\lim }\limits_{x \to {x_0}} \frac{{\frac{{x - {x_0}}}{{{x_0}}}}}{{x - {x_0}}} = 2x_0^2\mathop {\lim }\limits_{x \to {x_0}} \frac{1}{{{x_0}}}\\ = 2x_0^2.\frac{1}{{{x_0}}} = 2x\\ \Rightarrow \left( {{x^2}} \right)' = 2x\end{array}\)
b) Dự đoán đạo hàm của hàm số \(y = {x^n}\) tại điểm x bất kì: \(y' = n.{x^{n - 1}}\)
a) Tính đạo hàm của hàm số \(y = {x^3}\) tại điểm x bất kì.
b) Dự đoán công thức đạo hàm của hàm số \(y = {x^n}\left( {n \in {\mathbb{N}^*}} \right)\)
a) Với \({x_0}\) bất kì, ta có:
\(f'\left( {{x_0}} \right) = \mathop {\lim }\limits_{x \to {x_0}} \frac{{f\left( x \right) - f\left( {{x_0}} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \frac{{{x^3} - x_0^3}}{{x - {x_0}}}\\ = \mathop {\lim }\limits_{x \to {x_0}} \frac{{\left( {x - {x_0}} \right)\left( {{x^2} + x{x_0} + x_0^2} \right)}}{{x - {x_0}}} = \mathop {\lim }\limits_{x \to {x_0}} \left( {{x^2} + x{x_0} + x_0^2} \right) = 3x_0^2\)
Vậy hàm số \(y = {x^3}\) có đạo hàm là hàm số \(y' = 3{x^2}\)
b) \(y' = \left( {{x^n}} \right)' = n{x^{n - 1}}\)
Tính đạo hàm của hàm số y=10 tại điểm x=10?
\(y=10\) là hàm hằng nên \(y'=0\) với mọi x
Tính đạo hàm của hàm số y = 2 x 2 + x + 1 tại điểm x= 2
A. 9
B. 4
C. 7
D. 6
Tính đạo hàm của hàm số y = x 2 − x + 1 3 tại điểm x = − 1 .
A. 27
B. -27
C. 81
D. -81
Đáp án D
Ta có y ' = 3 x 2 − x + 1 2 2 x − 1 ⇒ y − 1 = − 81
Biết hàm số f ( x ) - f ( 2 x ) có đạo hàm bằng 5 tại x = 1 và đạo hàm bằng 7 tại x = 2 Tính đạo hàm của hàm số f ( x ) - f ( 4 x ) tại x = 1.
A. 8.
B. 12.
C. 16.
D. 19.
Cho hàm số y = 1 x − 3 . Tính đạo hàm cấp hai của hàm số đã cho tại x = 1?
A. y " ( 1 ) = − 1 4
B. y " ( 1 ) = 1 4
C. y " ( 1 ) = 1 6
D. y " ( 1 ) = − 1 6
Đáp án A
Ta có: y ' = − 1 ( x − 3 ) 2 . ( x − 3 ) ' = − 1 ( x − 3 ) 2 y " = − 1 ( x − 3 ) 2 ' = − − 1 ( x − 3 ) 4 = 1 ( x − 3 ) 4 .2 ( x − 3 ) = 2 ( x − 3 ) 3 ;
⇒ y " ( 1 ) = 2 ( 1 − 3 ) 3 = − 1 4 .