tìm dư trong phép chia
(x2005 + x2004) : (x2 - 1)
Tính giá trị của các biểu thức :
a) A = 5x5 - 5x4 + 5x3 - 5x2 + 5x - 1 tại x = 4.
b) B = x2006 – 8.x2005 + 8.x2004 - ...+8x2 - 8x – 5 tại x = 7.
x=4
=>x+1=5
A=(x+1)x^5 -(x+1)x^4+(x+1)x^3-(x+1)x^2+(x+1)x-1
=x^6+x^5-x^5-x^4+x^4+x^3-x^3-x^2+x^2-x+1
=x^6-x-1
=4^6-4-1
=4091
\(a,A=5\cdot4^5-5\cdot4^4+5\cdot4^3-5\cdot4^2+5\cdot4+1\\ A=4^4\left(20-5\right)+4^2\left(20-5\right)+\left(20-5\right)\\ A=15\left(4^4+4^2+1\right)=15\cdot273=4095\)
\(b,x=7\Leftrightarrow x+1=8\\ \Leftrightarrow B=x^{2006}-\left(x+1\right)x^{2005}+\left(x+1\right)x^{2004}-...+\left(x+1\right)x^2-\left(x+1\right)x-5\\ B=x^{2006}-x^{2006}-x^{2005}+x^{2005}+x^{2004}-...+x^3+x^2-x^2-x-5\\ B=-x-5=-12\)
b)tương tự
=x^2006-x^2006-x^2005+x^2005+x^2004-...+x^3-x^2-x^2-x-5
=-x-5
=-7-5=-12
Không làm phép chia, hãy tìm dư trong phép chia đa thức: x9+x6+x3+1 cho da thuc x2+x+1
Rõ ràng đa thức \(x^3-1\) chia hết cho đa thức \(x^2+x+1\).
Ta tách: \(x^9+x^6+x^3+1=\left(x^9-1\right)+\left(x^6-1\right)+\left(x^3-1\right)+4=\left(x^3-1\right)\left(x^6+x^3+1\right)+\left(x^3-1\right)\left(x^3+1\right)+\left(x^3-1\right)+4\).
Từ đây suy ra đa thức đó chia cho đa thức \(x^2+x+1\) được đa thức dư là 4.
Không chia có mà làm=niềm tin ah
Tìm dư của phép chia đa thức f(x) cho (x2 +1) (x-2) biết f(x) (chia x-2) dư 7 và f(x) : (x2 +1) dư 3x+5
Để tìm dư của phép chia đa thức f(x) cho (x^2 + 1)(x - 2), chúng ta cần sử dụng định lý dư của đa thức. Theo định lý dư của đa thức, nếu chia đa thức f(x) cho đa thức g(x) và được dư đa thức r(x), thì ta có: f(x) = q(x) * g(x) + r(x) Trong trường hợp này, chúng ta biết rằng f(x) chia cho x - 2 dư 7 và chia cho x^2 + 1 dư 3x + 5. Vì vậy, chúng ta có các phương trình sau: f(x) = q(x) * (x - 2) + 7 f(x) = p(x) * (x^2 + 1) + (3x + 5) Để tìm dư của phép chia f(x) cho (x^2 + 1)(x - 2), ta cần tìm giá trị của r(x). Để làm điều này, chúng ta cần giải hệ phương trình trên. Đầu tiên, chúng ta sẽ giải phương trình f(x) = q(x) * (x - 2) + 7 để tìm giá trị của q(x). Sau đó, chúng ta sẽ thay giá trị của q(x) vào phương trình f(x) = p(x) * (x^2 + 1) + (3x + 5) để tìm giá trị của p(x) và r(x). Nhưng trước tiên, chúng ta cần biết đa thức f(x) là gì. Bạn có thể cung cấp thông tin về đa thức f(x) không?
Tìm số dư trong phép chia của biểu thức:
( x + 1 )( x + 3 )( x + 5 )( x + 7 ) + 2004 cho x2 + 8x + 1.
Tìm x để phép chia ( 5 x 3 - 3 x 2 + 7 ) : ( x 2 + 1 ) có dư bằng 5
Tìm dư của phép chia đa thức x2022-x2021+2020 cho đa thức x2-1
Tìm x để phép chia sau có số dư bằng 0
( 2x4 - 3x3 + 4x2 +1) : x2 - 1
\(\dfrac{2x^4-3x^3+4x^2+1}{x^2-1}\)
\(=\dfrac{2x^4-2x^2-3x^3+3x+6x^2-6-3x+7}{x^2-1}\)
\(=2x^2-3x+6+\dfrac{-3x+7}{x^2-1}\)
Để đây là phép chia hết thì -3x+7=0
hay \(x=\dfrac{7}{3}\)
1,tìm số dư của 1994^2005:7
2,cmr :6^1001-1 và 6^1001+1 đều chia hết cho7
3,tìm số dư trong phép chia 1532^5-1:9
4,tìm số dư trong phép chia 3^2003:13
5,tìm số dư trong phép chia 7.5^2n+12.6^n:19 (n thuộc N)
Giải bằng phép đồng dư
Tìm x để phép chia (5x3 – 3x2 + 7) : ( x2 + 1) có dư bằng 5.
Ta có: \(\left(15x-6x+7\right):\left(2x+1\right)=5\)
Áp dụng định lý Bozout, ta có:
\(f\left(\frac{-1}{2}\right)=15\cdot\frac{-1}{2}-6\cdot\frac{-1}{2}+7=\frac{5}{2}\)
Vậy số dư là 2,5
Cho hai đa thức: A = 3x4 + x3 + 6x – 5 và B = x2 + 1. Tìm dư R trong phép chia A cho B rồi viết A dưới dạng A = B.Q + R
Thực hiện phép chia ta có:
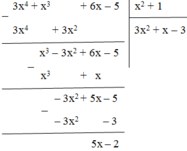
Vậy 3x4 + x3 + 6x – 5 = (x2 + 1).(3x2 + x – 3) + 5x – 2.