So sánh: A = a,b + 4,71 và B = a,71 + 4,b1 help
AD
Những câu hỏi liên quan
So sánh: A = a,b + 4,71 và B = a,71 + 4,b1
\(A=a,b+4,71=a+0,b+4+0,7+0,01\)
\(=\left(a+0,71\right)+\left(4+0,b+0,01\right)\)
\(=a,71+4,b1\)
mà \(B=a,71+4,b1\)
=> A=B
Đúng 2
Bình luận (1)
So sánh :
a. a,bd + 6,2c - 0,8d và a,64 + 2,b1 + 0,2c
b. a,bc - 2,9c + 7,5 và 4,b6 + a,53
a. Ta có:a,87 + 2.b2
=(a+0.87) + (0.b+2.02)
=(a+0.b) + (0.87+2.02)
=a.b + 2.89
Vì a.b + 2.89 = a.b + 2.89 nên a.87 + 2.b2 = a.b + 2.89
Đúng 0
Bình luận (0)
Trên hình biết a // b và góc B2=40 độ:
a) Tính góc A1
b) So sánh góc A3 và B1
c) Tính góc A2+B1
\(a,a//b\Rightarrow\widehat{B_2}+\widehat{A_1}=180^0\left(trong.cùng.phía\right)\\ \Rightarrow\widehat{A_1}=180^0-40^0=140^0\\ b,a//b\Rightarrow\widehat{A_1}=\widehat{B_1}\left(đồng.vị\right)\\ Mà.\widehat{A_1}=\widehat{A_3}\left(đối.đỉnh\right)\\ \Rightarrow\widehat{A_3}=\widehat{B_1}\\ c,Ta.có.\widehat{A_2}+\widehat{B_1}=\widehat{A_2}+\widehat{A_1}=180^0\left(kề.bù\right)\)
Đúng 1
Bình luận (1)
a. Ta có: a // b
=> \(\widehat{B_2}+\widehat{A_1}=180^o\) (2 góc trong cùng phía)
Mà \(\widehat{B_2}=40^o\)
=> \(\widehat{A_1}=180^o-40^o=140^o\)
b. Ta có: \(\widehat{A_1}=\widehat{B_3}\) (so le trong) (1)
Ta lại có: \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{A_3}\left(ĐĐ\right)\\\widehat{B_1}=\widehat{B_3}\left(ĐĐ\right)\end{matrix}\right.\) (2)
Từ (1) và (2), suy ra:
\(\widehat{A_3}=\widehat{B_1}\)
c. Ta có: a // b
=> \(\widehat{A_1}=\widehat{B_1}=140^o\) (đồng vị)
\(\widehat{B_2}=\widehat{A_2}=40^o\) (đồng vị)
=> \(\widehat{A_2}+\widehat{B_1}=140^o+40^o=180^o\)
Đúng 0
Bình luận (0)
cho hình vẽ biết góc A3+B1180 độ,hãy so sánh góc A4 và B1?,góc A1 và B2, Góc A2 và B3 x y B A 1 2 3 4 2 1 3 4
Đọc tiếp
cho hình vẽ biết góc A3+B1=180 độ,hãy so sánh góc A4 và B1?,góc A1 và B2, Góc A2 và B3
cho hình vẽBiết góc A3 +góc B1180 độhãy so sánh góc A4 và góc B1? A1 và góc B2? A2 và góc B3 x y B A m 1 2 4 3 2 1 3 4
Đọc tiếp
cho hình vẽ
Biết góc A3 +góc B1=180 độ
hãy so sánh góc A4 và góc B1?
A1 và góc B2?
A2 và góc B3
hình cho biết a//b và B1 = 40 độ a) Tính A4 b) So sánh A3 và B2 C) Tính B4
Cho hình vẽ bên, biết a // b và
B
^
2
45
0
a). Tính số đo
A
^
1
b). So sánh
A
^
3
và
B
^
1
c). Tính
A...
Đọc tiếp
Cho hình vẽ bên, biết a // b và B ^ 2 = 45 0
a). Tính số đo A ^ 1
b). So sánh A ^ 3 và B ^ 1
c). Tính A ^ 2 + B 1 ^
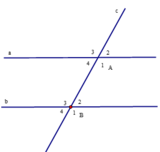
a) Vì B 2 ^ , A 1 ^ là cặp góc trong cùng phía nên ta có:
B 2 ^ + A 1 ^ = 180 0 ⇒ A 1 ^ = 180 0 − B 2 ^ = 180 0 − 45 0 = 135 0 .
b) Ta có B ^ 1 = A ^ 1 = 135 ∘ (hai góc đồng vị)
mà A ^ 3 = A ^ 1 = 135 ∘ (hai góc đối đỉnh)
Vậy B ^ 1 = A ^ 3 = 135 ∘
c) Ta có A ^ 1 + A ^ 2 = 180 ∘ (hai góc kề bù) mà B ^ 1 = A ^ 1 (theo câu b)
Do đó A ^ 2 + B ^ 1 = 180 ∘
Đúng 0
Bình luận (0)
so sánh A và B
A =a,64+2,15+2,b1+0,2c
B=a,bd+6,2-0,8d
Ta có: A= a,64+2,15+2,b1+0,2c
=> A= a+0,64+2,15+2+0,b+0,01+0,0c+0,2
=> A= ( a+0,b+0,0c)+(0,64+2,15+2+0,01+0,2)
=> A= a,bc+5
Lại có: B= a,bd+6,2-0,8d
=> B= a,bd+6,2- ( 0,8+0,0d)
=> B= a,bd+6,2-0,8-0,0d
=> B= a,bd+5,4-0,0d
=> B= a,b+5,4
nên xem lại đề pn ạ! Với kết quả này thì không chắc A hay B lớn hơn được đâu
Đúng 0
Bình luận (0)
Ta có :A=a+0,64+2,15+2+0,b+0,01+0,2+0,0c
=(a+0,b+0,0c)+(0,64+2,15+2+0,01+0,2)
=a,b+0,0c+5
B=a,b+0,0d+6,2-(0,8+0,0d)
=a,b+0,0d+6,2-0,8-0,0d
=a,b+(6,2-0,8)+(0,0d-0,0d)
=a,b+5,4+0
=a,b+5+0,4
Vì A và B đều có chung biểu thức a,b + 5 mà 0,0c < 0,4 nên A < B.
Vậy A < B.
Đúng 1
Bình luận (0)
Hình 22 cho biết a // b và A4 = 37'( độ )
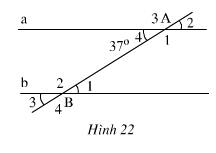
a) Tính B1
b) So sánh A1 và B4
c) Tính B2
a, a//b \(\Rightarrow\widehat{A_4}=\widehat{B_1}=37^0\left(so.le.trong\right)\)
b, a//b \(\Rightarrow\widehat{A_1}=\widehat{B_4}\left(đồng.vị\right)\)
c, \(\widehat{B_2}+\widehat{B_1}=180^0\left(kề.bù\right)\Rightarrow\widehat{B_2}=180^0-37^0=143^0\)
Đúng 3
Bình luận (1)
a) Ta có: a//b
⇒A4=B1=370(so le trong)
b) Ta thấy a//b
A1 và B4 là 2 góc đồng vị
⇒A1=B4
c) Ta lại có: A4+B2=1800(trong cùng phía)
⇒370+B2=1800
⇒B2=1800-370=1430
Đúng 3
Bình luận (0)






