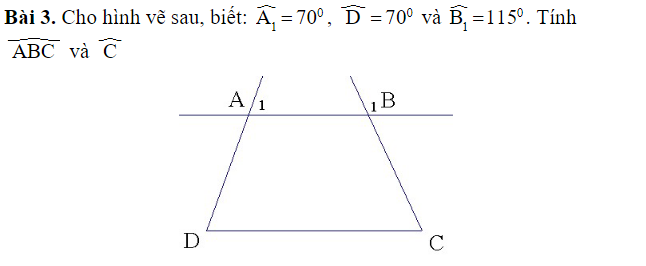
\(a,a//b\Rightarrow\widehat{B_2}+\widehat{A_1}=180^0\left(trong.cùng.phía\right)\\ \Rightarrow\widehat{A_1}=180^0-40^0=140^0\\ b,a//b\Rightarrow\widehat{A_1}=\widehat{B_1}\left(đồng.vị\right)\\ Mà.\widehat{A_1}=\widehat{A_3}\left(đối.đỉnh\right)\\ \Rightarrow\widehat{A_3}=\widehat{B_1}\\ c,Ta.có.\widehat{A_2}+\widehat{B_1}=\widehat{A_2}+\widehat{A_1}=180^0\left(kề.bù\right)\)
a. Ta có: a // b
=> \(\widehat{B_2}+\widehat{A_1}=180^o\) (2 góc trong cùng phía)
Mà \(\widehat{B_2}=40^o\)
=> \(\widehat{A_1}=180^o-40^o=140^o\)
b. Ta có: \(\widehat{A_1}=\widehat{B_3}\) (so le trong) (1)
Ta lại có: \(\left\{{}\begin{matrix}\widehat{A_1}=\widehat{A_3}\left(ĐĐ\right)\\\widehat{B_1}=\widehat{B_3}\left(ĐĐ\right)\end{matrix}\right.\) (2)
Từ (1) và (2), suy ra:
\(\widehat{A_3}=\widehat{B_1}\)
c. Ta có: a // b
=> \(\widehat{A_1}=\widehat{B_1}=140^o\) (đồng vị)
\(\widehat{B_2}=\widehat{A_2}=40^o\) (đồng vị)
=> \(\widehat{A_2}+\widehat{B_1}=140^o+40^o=180^o\)