Tính A biết Ax1,25=2,75+1,25x9
nhanh nha mình đang cần nộp gấp
Có bạn nào biết làm thi giúp mfinh câu này nha mình đang cần gấp 9 giờ là mình phải nộp cho thầy rồi thầy này cực khó tính nếu được mình cảm ơn rất rất nhiều
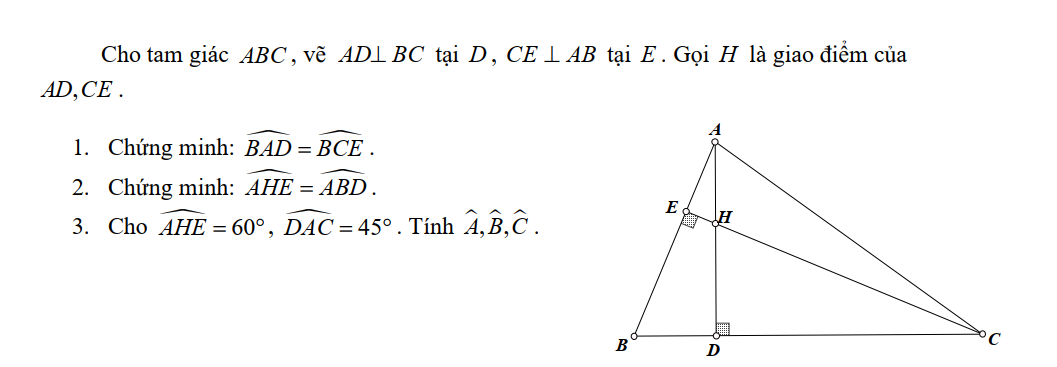
1: Ta có: \(\widehat{BAD}+\widehat{B}=90^0\)
\(\widehat{BCE}+\widehat{B}=90^0\)
Do đó: \(\widehat{BAD}=\widehat{BCE}\)
2: Ta có: \(\widehat{AHE}+\widehat{BAD}=90^0\)
\(\widehat{ABD}+\widehat{BAD}=90^0\)
Do đó: \(\widehat{AHE}=\widehat{ABD}\)
câu 3:
Xét tam giác AEH vuông tại E: góc AHE+ góc EAH= 90 độ
60 độ +góc EAH=90 độ
góc EAH=30 độ (1)
Ta có: góc A= góc EAH+ góc HAC= 30 độ +45 độ= 75 độ
Xét tam giác ADB vuông tại D có: góc B + góc EAH= 90 độ
góc B= 90 độ - 30 độ= 60 độ
lại có: góc BAC+ góc B + góc ACB= 180 độ (đ/ lý tổng ba góc trong 1 tam giác)
=> góc ACB= 180 độ-( 75 độ + 60 độ )= 45 độ
Tính nhanh:
450% + 3 và 1/4 - 2,75 + 2 và 3/10 + 2,7
Mọi người giúp mình nhanh nhé! Mình đang cần gấp.
1. \(450\%+3=\dfrac{9}{2}+3=\dfrac{15}{2}\)
2. \(\dfrac{1}{4}-2,75+2=0,25-2,75+2=-0,5\)
3. \(\dfrac{3}{10}+2,7=0,3+2,7=3\)
Có bạn nào biết làm câu này thì giúp mình nha mình đang cần gấp 4 giờ mình phải nộp rồi.Mình cảm ơn nhiều
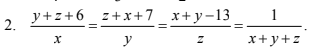
Có bạn nào biết làm câu này thì giúp mình nha mình đang cần gấp 11 gờ mình phải nộp cho thầy rồi nếu được thì mình cảm ơn nhiều

1: Xét ΔAOC và ΔBOD có
OA=OB
\(\widehat{AOC}=\widehat{BOD}\)
OC=OD
Do đó: ΔAOC=ΔBOD
Suy ra: \(\widehat{ACO}=\widehat{BDO}\)
mà hai góc này là hai góc ở vị trí so le trong
nên AC//BD
Có bạn nào biết làm câu này thì giúp mình nha mình đang cần gấp 11 gờ mình phải nộp cho thầy rồi nếu được thì mình cảm ơn nhiều
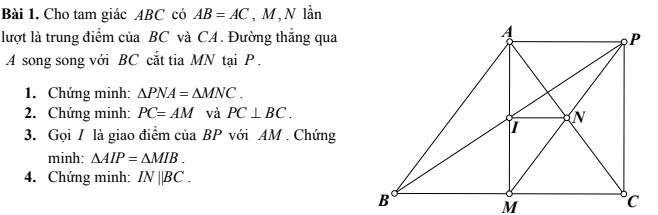
1. Vì N là trung điểm của AC do đó AN = CN
Ta có P là điểm kéo dài từ A cắt tia MN nên M, N, P là 3 điểm thẳng hàng
\(\Rightarrow\)N là trung điểm của MP và MN = NP
Xét \(\Delta PNA\) và \(\Delta MNC\) ta có :
AN = NC (cmt)
\(\widehat{PNA}\) = \(\widehat{MNC}\) ( hai góc đối đỉnh )
MN = NP (cmt)
\(\Rightarrow\Delta PNA=\Delta MNC\) ( c.g.c )
\(\Rightarrow AP=MC\) ( hai cạnh tương ứng )
2. Xét \(\Delta ANM\) và \(\Delta PNC\) ta có :
AN = NC (cmt)
\(\widehat{ANM}\) = \(\widehat{PNC}\) ( hai góc đối đỉnh )
MN = NP (cmt)
\(\Rightarrow\Delta ANM=\Delta PNC\) ( c.g.c )
\(\Rightarrow AM=PC\) ( hai cạnh tương ứng )
\(\Rightarrow AM\)//\(PC\)
Vì \(\Delta ABC\) có AB = AC nên \(\Delta ABC\) là tam giác cân tại A
Mà M là trung điểm của BC \(\Rightarrow BM=MC\) nên AM là đường trung trực của đoạn thẳng BC hay AM ⊥ BC
Áp dụng theo quan hệ giữa tính vuông góc và tính song song "nếu a//b và c⊥a thì b⊥c"
Từ đó ta suy ra PC ⊥ BC
2. Vì AP = MC nên AP = BM ( cùng MC )
Điểm I được nối qua N và nằm trên đoạn thẳng AM nên ba điểm A, I, M thẳng hàng ⇒ I là trung điểm của AM và AI = IM
Xét \(\Delta AIP\) và \(\Delta MIB\) ta có :
AP = PM (cmt)
AI = IM (cmt)
\(\Rightarrow\Delta AIP=\Delta MIB\) ( trường hợp bằng nhau hai cạnh góc vuông của tam giác vuông )
*Thưa bạn, câu 4 mình không biết giải nên mong bạn thông cảm. Nếu bài mình có chỗ nào không đúng thì bạn sửa lại giúp mình nhé!
4: Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC
Có bạn nào biết làm câu này thì giúp mình nha mình đang cần gấp 111 gờ mình phải nộp cho thầy rồi nếu được thì mình cảm ơn nhiều
1: Xét ΔABC có AB=AC
nên ΔBAC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
Ta có: ΔABC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH là đường cao ứng với cạnh BC
Có bạn nào biết làm thì giúp mình nha mình đang cần gấp 9 giờ tối hôm nay mình phải nộp rồi nếu được thì mình cảm ơn rất rất nhiều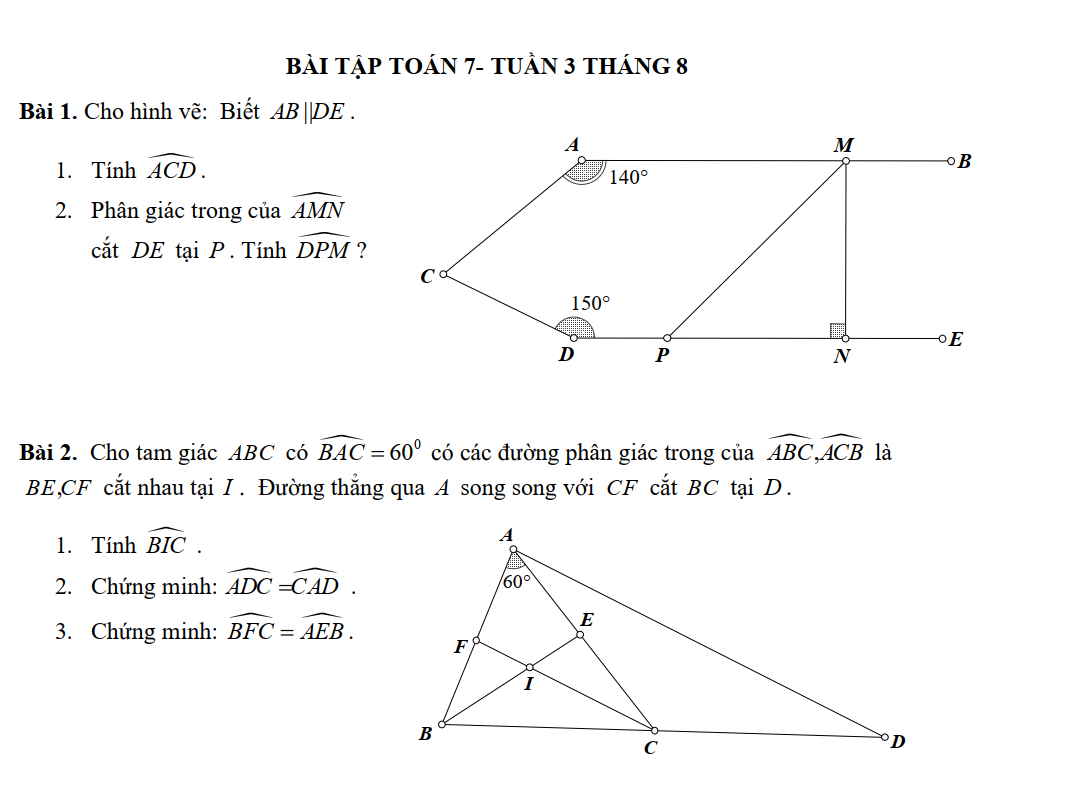
Bài 1:
1) Kẻ tia Cx//AB//DE
Ta có: Cx//AB
\(\Rightarrow\widehat{BAC}+\widehat{ACx}=180^0\)(2 góc trong cùng phía)
\(\Rightarrow\widehat{ACx}=180^0-\widehat{BAC}=180^0-140^0=40^0\)
Ta có: Cx//DE
\(\Rightarrow\widehat{xCD}+\widehat{CDE}=180^0\)( 2 góc trong cùng phía)
\(\Rightarrow\widehat{xCD}=180^0-\widehat{CDE}=180^0-150^0=30^0\)
\(\Rightarrow\widehat{ACD}=\widehat{ACx}+\widehat{xCD}=40^0+30^0=70^0\)
2) Ta có AB//DE(gt)
Mà DE⊥MN
=> AB⊥MN =>\(\widehat{AMN}=90^0\Rightarrow\dfrac{1}{2}\widehat{AMN}=45^0\Rightarrow\widehat{AMP}=45^0\) (do MP là tia phân giác \(\widehat{AMN}\))
Ta có AB//DE
=> \(\widehat{AMP}+\widehat{DPM}=180^0\) (2 góc trong cùng phía)
\(\Rightarrow\widehat{DPM}=180^0-\widehat{AMP}=180^0-45^0=135^0\)
Xét tam giác BIC có:
a)\(\widehat{BIC}=180^0-\left(\widehat{IBC}+\widehat{ICB}\right)=180^0-\left(\dfrac{\widehat{ABC}}{2}+\dfrac{\widehat{ACB}}{2}\right)=180^0-\dfrac{180^0-\widehat{BAC}}{2}=180^0-\dfrac{180^0-60^0}{2}=120^0\)
b) Ta có: FC//AD(gt)
\(\Rightarrow\left\{{}\begin{matrix}\widehat{FCB}=\widehat{ADC}\\\widehat{CAD}=\widehat{ACF}\end{matrix}\right.\)
Mà \(\widehat{FCB}=\widehat{ACF}\)(CF là tia phân giác \(\widehat{ACB}\))
\(\Rightarrow\widehat{ADC}=\widehat{CAD}\)
c) Xét tam giác BFI có:
\(\widehat{BFC}+\widehat{ABI}=\widehat{BIC}=120^0\left(1\right)\)(tính chất góc ngoài tam giác)
Xét tam giác ABE có:
\(\widehat{BAC}+\widehat{AEB}+\widehat{ABI}=180^0\)(tổng 3 góc trong tam giác)
\(\Rightarrow\widehat{AEB}+\widehat{ABI}=180^0-\widehat{BAC}=180^0-60^0=120^0\left(2\right)\)
Từ \(\left(1\right),\left(2\right)\Rightarrow\widehat{BFC}=\widehat{AEB}\)
Có bạn nào biết làm câu này thì giúp mình nha mình đang cần cực gấp 11 giờ mình phải nộp cho thầy rồi(chỉ cònn 2 tiếng gấp lắm rồi) nếu được thì mình cảm ơn rất rất nhiều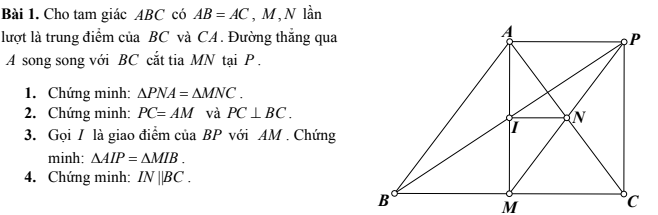
4: Xét ΔAMC có
I là trung điểm của AM
N là trung điểm của AC
Do đó: IN là đường trung bình của ΔAMC
Suy ra: IN//MC
hay IN//BC
Có bạn nào biết làm câu này thì giúp mình nha mình đang cần cực gấp 11 giờ mình phải nộp cho thầy rồi(chỉ cònn 2 tiếng gấp lắm rồi) nếu được thì mình cảm ơn rất rất nhiều
1: Xét ΔABC có AB=AC
nên ΔABC cân tại A
Suy ra: \(\widehat{B}=\widehat{C}\)
Ta có: ΔBAC cân tại A
mà AH là đường trung tuyến ứng với cạnh đáy BC
nên AH là đường cao ứng với cạnh BC