Tính tổng các phân số tối giản lớn hơn 15 và nhỏ hơn 30 biết mẫu của chúng bằng 17
cho hai số tự nhiên a và b (a<b). Tìm tổng các phân số tối giản có mẫu bằng 7, mỗi phân số lớn hơn a nhưng nhỏ hơn b
cho hai số tự nhiên a và b (a<b). Tìm tổng các phân số tối giản có mẫu bằng 7, mỗi phân số lớn hơn a nhưng nhỏ hơn b
Gọi A là tập hợp các phân số tối giản nhỏ hơn 1 có tử và mẫu đều dương, biết tích của tử và mẫu của phân số đó bằng 120. Số phần tử của tập hơn A là ?
mình thi Violympic cáp tỉnh mắc nhõn câu này !!!
4 phần tử nha chú ý câu hỏi hỏi số pt cơ mà
1 . Viết tất cả phân số bé hơn 1 có tổng tử số và mẫu số bằng 10
2. Viết tất cả các phân số tối giản có tử số và mẫu số bằng 20
1 + 9 = 10
2 + 8 = 10
3 + 7 = 10
4 + 6 = 10
Có thể lập tất cả: 1/9 ; 2/8 ; 3/7 ; 4/6
Tìm 3 phân số tối giản biết: các tử số tỉ lệ với 2,3,4 và mẫu số tỉ lệ với 3,5,4. Và tổng của 3 phân số đó bằng \(\frac{133}{60}\).
tìm 3 phân số tối giản biết tổng của chúng bằng 12\(\frac{7}{24}\) tử số của chúng tỉ lệ với 3,5,7. mẫu của chúng tỉ lệ với 2,3,4
Tìm các phân số tối giản có mẫu khác 1, biết rằng tích của tử và mẫu bằng 3150 và phân số này có thể viết được dưới dạng số thập phân hữu hạn.
Gọi phân số tối giản phải tìm là a/b; (a; b ∈ Z; b ≠ 1), ƯCLN (a, b) = 1
Ta có a.b = 3150 = 2. 32. 52. 7 và a, b đều là ước của 3150.
Vì phân số này có thể viết được dưới dạng số thập phân hữu hạn nên b chỉ có ước nguyên tố là 2 và 5.
Do đó, b ∈ {2; 25; 50}.
- Với b = 2 thì a = 3150:2 = 1575
- Với b = 25 thì a = 3150:25 = 126
- Với b = 50 thì a = 3150:50 = 63
Vậy các phân số phải tìm là:
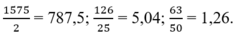
Tìm 2 phân số tối giản. Biết hiệu của chúng là 3/196 và các tử tỉ lệ với 3; 5 và các mẫu tỉ lệ với 4; 7
gọi 2 phân số đó là \(\frac{a}{b}\) và \(\frac{c}{d}\)
theo đề ta có:
\(\frac{a}{b}-\frac{c}{d}=\frac{3}{196}\) (1)
\(\frac{a}{c}=\frac{3}{5}=>a=\frac{3c}{5}\) (2)
\(\frac{b}{d}=\frac{4}{7}=>b=\frac{4d}{7}\) (3)
lấy (2) và (3) thay vào (1) ta có:
\(\frac{21c}{20d}-\frac{c}{d}=\frac{3}{196}\)
\(=>\frac{c}{d}=\frac{16}{49}\)
thay vào (1): \(\frac{a}{b}=\frac{9}{28}\)
=> 2 phân số cần tìm là \(\frac{15}{49}va\frac{9}{28}\)
Gọi 2 phân số cần tìm là a/b và c/d.
- Giả sử a/b > c/d
Theo đề bài, ta có:
{a : c = 3 : 5
{b : d = 4 : 7
<=> Tỉ số của 2 phân số là: a/b : c/d = 3/4 : 5/7
<=> a/b . d/c = 3/4 . 7/5
<=> ad / bc = 21/20
<=> ad = 21/20 . bc = (21bc)/20
Ta lại có:
a/b - c/d = (ad - bc)/bd = 3/196
<=> [(21bc) / 20 - bc] / bd = 3/196
<=> [(21bc) / 20] / bd - bc / bd = 3/196
<=> (21bc) / 20 . 1 / bd - bc / bd = 3/196
<=> 21c / 20d - c / d = 3/196
<=> 21c / 20d - 20c / 20d = 3/196
<=> c / 20d = 3/196
=> c : 3 và 20d : 196 => c : 3 và d : 196/20 => c : 3 và d : 49/5
<=> c/d = 3 : 49/5 = 3 . 5 : 49 = 15/49
=> c = 15 ; d = 49
=> a : c = 3 : 5 => a : 15 = 3 : 5 => a = 9
và b : d = 4 : 7 => b : 49 = 4 : 7 => b = 28
=> a/b = 9/28 và c/d = 15/49
Thử lại, a/b - c/d = 9/28 - 15/49 = 3/196 (đúng theo yêu cầu đề bài)
- Do đó, 2 phân số cần tìm là 9/28 và 3/196
bài của mk là đúng dax
thầy mk nói là dg rồi
Tìm các phân số tối giản có mẫu khác 1 biết rằng tích của tử và mẫu bằng 3150 và phân số này có thể viết được dưới dạng số thập phân hữu hạn