Các phân số/;1/5;3/2;1/4 được xếp theo thứ tự từ lớn đến bé là
H24
Những câu hỏi liên quan
Cho các phân số:a) Rút gọn phân số:b) Viết các phân số đều có mẫu số là 40 và bằng các phân số đã cho:c)Trong các phân số trên có những phân số bằng nhau là:
Đọc tiếp
Cho các phân số: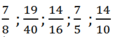
a) Rút gọn phân số:

b) Viết các phân số đều có mẫu số là 40 và bằng các phân số đã cho:
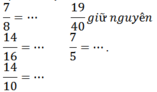
c)Trong các phân số trên có những phân số bằng nhau là:
a) Rút gọn phân số:

b) Viết các phân số đều có mẫu số là 40 và bằng các phân số đã cho:
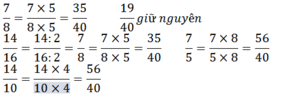
c)Trong các phân số trên có những phân số bằng nhau là:
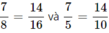 và
và 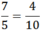
Đúng 0
Bình luận (0)
Trong các phân số sau: D Ca) Các phân số lớn hơn 1 là:……………………….b) Các phân số bé hơn 1 là:……………………….c) Các phân số bằng 1 là:……………………….d) Các phân số bằng 0 là:……………………….
Đọc tiếp
Trong các phân số sau: D C
![]()
a) Các phân số lớn hơn 1 là:……………………….
b) Các phân số bé hơn 1 là:……………………….
c) Các phân số bằng 1 là:……………………….
d) Các phân số bằng 0 là:……………………….
cho các phân số 7/30, 9/300, 15/75, 41/900, 10/41. trong các phân số đã cho , phân số nào có thể chuyển thành phân số thập phân ? hãy chuyển các phân số đó thành các phân số thập phân.
Phân số 9/300 có thể chuyển về số thập phân là:0,03
Đúng 1
Bình luận (0)
1.Viết các phân số sau dưới dạng hỗn số : 2. Viết các hỗn số sau dưới dạng phân số :3. So sánh các phân số : 22/7 và 34/114. Viết các phân số sau dưới dạng số thập phân và dùng kí hiệu % :5. Viết các phần trăm sau dưới dạng số thập phân : 7% ; 45% ; 216%.6. Tìm số nghịch đảo của các số sau :7. Đổi ra mét (viết kết quả dưới dạng phân số thập phân rồi dưới dạng số thập phân):3dm , 85cm , 52mm.
Đọc tiếp
1.Viết các phân số sau dưới dạng hỗn số :

2. Viết các hỗn số sau dưới dạng phân số :

3. So sánh các phân số : 22/7 và 34/11
4. Viết các phân số sau dưới dạng số thập phân và dùng kí hiệu % :
![]()
5. Viết các phần trăm sau dưới dạng số thập phân : 7% ; 45% ; 216%.
6. Tìm số nghịch đảo của các số sau :

7. Đổi ra mét (viết kết quả dưới dạng phân số thập phân rồi dưới dạng số thập phân):
3dm , 85cm , 52mm.
Bài 1
\(\dfrac{6}{5}\)=\(1\dfrac{1}{5}\)
\(\dfrac{7}{3}\)=\(2\dfrac{1}{3}\)
\(-\dfrac{16}{11}\)=\(-1\dfrac{5}{11}\)
Bài 2 :
\(5\dfrac{1}{7}\)=\(\dfrac{5.7+1}{7}\)=\(\dfrac{36}{7}\)( Dấu " . " là dấu nhân )
\(6\dfrac{3}{4}\)=\(\dfrac{6.4+3}{4}\)=\(\dfrac{27}{4}\)
\(-1\dfrac{12}{13}\)=\(-\dfrac{25}{13}\)
Bài 3 :
Chuyển phân số về hỗn số
Bài 4 :
Sorry Mình không biết làm:(
Bài 5 :
7%=\(\dfrac{7}{100}\)
45%=\(\dfrac{9}{20}\)
216%=\(\dfrac{54}{25}\)
Bài 6 :
\(\dfrac{3}{7}\)=\(\dfrac{7}{3}\)
\(6\dfrac{1}{3}\)=\(\dfrac{19}{3}\)=\(\dfrac{3}{19}\)
\(\dfrac{-1}{12}\)=\(\dfrac{-12}{1}\)
Bài 7 :
3dm=\(\dfrac{3}{10}\)m=0,3m
85cm=\(\dfrac{85}{100}\)m=0,85m
52mm=\(\dfrac{52}{1000}\)m=0,052m
Nếu có sai sót gì thì nói nhắn tin với mình
Đúng 1
Bình luận (0)
Xem thêm câu trả lời
Bài 3:Viết các phân số thích hợp vào chỗ chấm:
Trong các phân số: ; ; ; ; ;
a) Các phân số bé hơn 1 là:.......................................................................................
b) Các phân số bằng 1 là:..........................................................................................
c) Các phân số lớn hơn 1 là:
Đọc tiếp
Bài 3:Viết các phân số thích hợp vào chỗ chấm:
Trong các phân số: ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]() ;
; ![]()
a) Các phân số bé hơn 1 là:.......................................................................................
b) Các phân số bằng 1 là:..........................................................................................
c) Các phân số lớn hơn 1 là:
Từ các số tự nhiên 2,3,4,5. Hãy viết:
a, Các phân số bé hơn 1.
b, Các phân số bằng 1.
c, Các phân phân số lớn hơn 1.
Mong các bn giải giúp mình.
a. Các phân số bé hơn 1:
2/3 ; 3/4; 4/5; 2/4; 2/5; 3/5
b. Các phân số lớn hơn 1:
3/2; 4/3; 5/4 ; 4/2; 5/2; 5/3
c. Các phân số bằng 1:
2/2; 3/3; 4/4; 5/5
Đúng 1
Bình luận (0)
Cho các phân số trên: 3/5; -6/9; 3-5/-4; 8/-5a) Tìm các phân số tối giản từ các phân số trên ( không giải thích)b) Rút gọn các phân số chưa tối giản từ các phân số trên c) Tìm các phân số dương, các phân số âm từ các phân số trên ( không giải thích) Các bạn giúp mik cáiMai thi rồi 🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️
Đọc tiếp
Cho các phân số trên: 3/5; -6/9; 3-5/-4; 8/-5
a) Tìm các phân số tối giản từ các phân số trên ( không giải thích)
b) Rút gọn các phân số chưa tối giản từ các phân số trên
c) Tìm các phân số dương, các phân số âm từ các phân số trên ( không giải thích)
Các bạn giúp mik cái
Mai thi rồi 🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️🙆♀️
Cho các phân số sau:
3
5
;
2
3
;
7
10
;
27
50
. Trong các phân số trên, phân số nào là phân số thập phân? A.
3
5
B.
2
3
C.
7
10
D.
27
50
Đọc tiếp
Cho các phân số sau: 3 5 ; 2 3 ; 7 10 ; 27 50 . Trong các phân số trên, phân số nào là phân số thập phân?
A. 3 5
B. 2 3
C. 7 10
D. 27 50
Các phân số có mẫu số là 10,100,1000 được gọi là phân số thập phân.
Mà trong các phân số trên ta thấy số phân số 7 10 có mẫu số la 10. Vậy phân số 7 10 là phân số thập phân.
Đáp án cần chọn là C
Đúng 0
Bình luận (0)
Cho các phân số thoả mẫn tích các phân số đó là một nguyên và tống hai phân số bất kỳ trong các phân số đó cũng là sồ nguyên. Chứng minh rằng tất cả các phân số đã cho đều nguyên.
Gọi \(q_1,q_2,...,q_n\left(q_i\inℚ,\forall i=\overline{1,n}\right)\). Theo đề bài, ta có \(q_1q_2...q_n\inℤ\) và \(q_i+q_j\inℤ,\forall i\ne j;i,j=\overline{1,n}\). Không mất tính tổng quát, giả sử \(q_1< q_2< ...< q_n\)
Ta thấy \(q_1+q_2\inℤ\) và \(q_2+q_3\inℤ\) nên \(q_1-q_3\inℤ\). Mà \(q_1+q_3\inℤ\) nên nếu ta đặt \(q_1-q_3=v\) và \(q_1+q_3=u\) với \(u,v\inℤ\) thì \(q_1=\dfrac{u+v}{2};q_3=\dfrac{u-v}{2}\). Do \(q_1+q_2=\dfrac{u+v+2q_2}{2}\) và \(q_3+q_2=\dfrac{u-v+2q_2}{2}\) cũng là các số nguyên, hơn nữa \(u-v\equiv u+v\left(mod2\right)\) nên ta chỉ cần suy ra \(u+v+2q_1⋮2\) hay \(u+v\) là số chẵn, cũng tức là \(q_1=\dfrac{u+v}{2}\) là số nguyên. Một cách tương tự, ta sẽ chứng minh được \(q_i\inℤ,\forall i=\overline{1,n}\) (đpcm)
Đúng 2
Bình luận (0)





