Đường phân giác của 1 góc là đường thẳng chứa tia phân giác của góc đó
VN
Những câu hỏi liên quan
1. Cho tam giác ABC, góc A 120 độ, AA, BB, CC theo thứ tự là tia phân giác của các góc A, B, C. CMR AB vuông góc với AC.2. Cho tam giác ABC cân ở A. Kẻ tia phân giác BD của góc B và tia phân giác DM của góc BDC, đường phân giác của góc ADB cắt đường thẳng BC tại N. CMR BD 1/2 MN.3. Từ đỉnh A của tam giác ABC, kẻ các đường vuông góc xuống các tia phân giác trong và ngoài của các góc tại đỉnh B và C. CMR chân các đường vuông góc đó thẳng hàng.
Đọc tiếp
1. Cho tam giác ABC, góc A = 120 độ, AA', BB', CC' theo thứ tự là tia phân giác của các góc A, B, C. CMR A'B' vuông góc với A'C'.
2. Cho tam giác ABC cân ở A. Kẻ tia phân giác BD của góc B và tia phân giác DM của góc BDC, đường phân giác của góc ADB cắt đường thẳng BC tại N. CMR BD = 1/2 MN.
3. Từ đỉnh A của tam giác ABC, kẻ các đường vuông góc xuống các tia phân giác trong và ngoài của các góc tại đỉnh B và C. CMR chân các đường vuông góc đó thẳng hàng.
Cho AOB=80 độ có . Gọi góc AOC và góc BOD là các góc kề bù với góc AOB. Chứng minh rằng:
a)Hai góc AOC và BOD là hai gócđối đỉnh.
b)Đường thẳng chứa tia phân giác của góc BOD cũng chứa tia phân giác của AOC
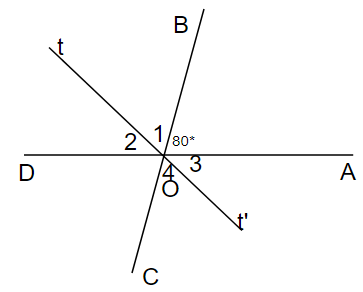
a) Vì ∠AOC kề bù với ∠AOB
⇒ OC và OB là 2 tia đối nhau và ∠AOC + ∠AOB = 1800
Vì ∠BOD và ∠AOB là 2 tia đối nhau
⇒ OA và OD là 2 tia đối nhau và ∠BOD + ∠AOB = 180o
⇒ ∠AOC = ∠BOD
Vì ∠AOC có OA là tia đối của tia OD;
∠BOD có OC là tia đối của tia OB
Mà ∠AOC = ∠BOD
⇒ ∠AOC và ∠BOD là 2 góc đối đỉnh
b) Gọi Ot là tia phân giác của ∠BOD
⇒ ∠O1 = ∠O2 = ∠BOD/2
Gọi Ot' là tia đối của tia Ot có OB là tia đối của tia OC
⇒ ∠O1 = ∠O4 (đối đỉnh)
Tia OD là tia đối của tia OA
⇒ ∠O2 = ∠O3 (đối đỉnh)
⇒ ∠O3 = ∠O4 = ∠BOD/2 = ∠AOC /2
⇒ Ot' là tia phân giác của ∠AOC
Mà Ot và Ot' đối nhau
⇒ Ot và Ot' cùng nằm trên 1 đường thẳng (đpcm)
Đúng 1
Bình luận (2)
Cho tam giác ABC . Vẽ đường thẳng b chứa tia phân giác góc ngoài tại đỉnh B và đường thẳng c chứa tia phân giác góc ngoài tại đỉnh C . Hai đường thẳng b và c cắt nhau tại O .Từ A vẽ đường thẳng vuông góc với b và c chúng cắt đường thẳng BC lần lượt tại M và N . Vẽ đường thẳng a là đường trung trực của MN . CMR : a) Chu vi tam giác ABC MNb) Ba đường thẳng a,b,c cùng đi qua điểm O c) Tia OA là tia phân giác góc BAC .
Đọc tiếp
Cho tam giác ABC . Vẽ đường thẳng b chứa tia phân giác góc ngoài tại đỉnh B và đường thẳng c chứa tia phân giác góc ngoài tại đỉnh C . Hai đường thẳng b và c cắt nhau tại O .Từ A vẽ đường thẳng vuông góc với b và c chúng cắt đường thẳng BC lần lượt tại M và N . Vẽ đường thẳng a là đường trung trực của MN . CMR :
a) Chu vi tam giác ABC = MN
b) Ba đường thẳng a,b,c cùng đi qua điểm O
c) Tia OA là tia phân giác góc BAC .
Câu 1: Cho tam giác ABC , ( B > C) Đường thẳng chứa tia phân giác ngoài tại đỉnh A cắt đường thẳng BC tại N. Tia phân giác trong của góc A cắt BC tại m. Chứng minh rằng góc ANC = góc AMC - góc AMB chia 2
Bài 1:Hai đường thảng AB và CD cắt nhau tại E tạo thành bốn góc không kể góc bẹt.Biết tổng của ba trong bốn góc này bằng 250 độ ,tính số đo của bốn góc đó.
Bài 2:Cho góc AOB =80 độ.Gọi góc AOC và BOD là các góc kề bù với góc AOB.CMR:
a)Hai góc AOC và Bod là hai góc đối đỉnh
b)Đường thẳng chứa tia phân giác của góc BOD cũng chứa tia phân giác của AOC
mk cũng đang gặp câu này giups mk với các bạn
Đúng 0
Bình luận (0)
Chứng minh rằng trong một tam giác, tia phân giác của một góc trong và hai tia phân giác của hai góc ngoài không kề với nó đồng quy tại một điểm, điểm đó cách đều ba đường thẳng chứa ba cạnh của tam giác.
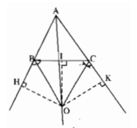
Giả sử hai tia phân giác của các góc ngoài tại đỉnh B và C của tam giác ABC cắt nhau tại O. Ta sẽ chứng minh AO là tia phân giác của góc A.
Kẻ các đường vuông góc OH, OI, OK từ O lần lượt đến các đường thẳng AB, BC, AC.
Vì BO là tia phân giác của góc HBC nên OH = OI (1)
Vì CO là tia phân giác của góc KCB nên OI = OK (2)
Từ (1) và (2) suy ra OI = OH = OK
(3)
Suy ra: O thuộc đường phân giác của góc BAC.
Suy ra AO là tia phân giác của góc BAC và ta có điều phải chứng minh.
Đúng 1
Bình luận (0)
Trên cùng một nửa mặt phẳng bờ là đường thẳng chứa tia Oa, vẽ hai tia Ob và Oc sao cho góc aOb= 100o, góc aOc= 150o.
Vẽ tia Om là tia phân giác của góc aOb, chứng tỏ rằng tia Ob là tia phân giác của góc mOc
Cho tam giác ABC. Vẽ đường thẳng b chứa tia phân giác góc ngoài tại đỉnh B và đường thẳng c chứa tia phân giác góc ngoài tại đỉnh C. Hai đường thẳng b và c cắt nhau tại O. Từ A vẽ đường thẳng vuông góc b,c. Chúng cắt đường thẳng b,c tại M,N. Vẽ đường thẳng a là đường trung trực của MN.CM: a) chu vi tam giác ABC MN b) 3 đt a,b,c cùng đi qua O c) Tia AO là phân giác góc BAC
Đọc tiếp
Cho tam giác ABC. Vẽ đường thẳng b chứa tia phân giác góc ngoài tại đỉnh B và đường thẳng c chứa tia phân giác góc ngoài tại đỉnh C. Hai đường thẳng b và c cắt nhau tại O. Từ A vẽ đường thẳng vuông góc b,c. Chúng cắt đường thẳng b,c tại M,N. Vẽ đường thẳng a là đường trung trực của MN.CM: a) chu vi tam giác ABC = MN
b) 3 đt a,b,c cùng đi qua O
c) Tia AO là phân giác góc BAC
Mọi người ơi mk cx đang thắc mắc bài toán này . Giải dùm mk vs . Cảm ơn nhìu . Mong các bạn giúp đỡ .😣😑🔊🤐😕🙊🙋✌👌👍💖
Đúng 0
Bình luận (0)
Chứng minh rằng trong một tam giác, tia phân giác của một góc trong và hai tia phân giác của hai góc ngoài không kề với nó đồng quy tại một điểm, điểm đó cách đều ba đường thẳng chứa ba cạnh của tam giác ?


