Mọi người giải thích giúp em với ạ
mọi người giúp em giải x với ạ ( mọi người ghi giải thích giúp e với ạ)
818=3x
`81^8=3^x`
`=>3^x=(3^4)^8`
`=>3^x=3^32`
`=>x=32`
Vậy `x=32`
\(81^8=3^x\)
\(\Leftrightarrow\left(3^4\right)^8=3^x\)
\(\Leftrightarrow3^{32}=3^x\)
\(\Leftrightarrow x=32\)
Mọi người giải giúp em bài này với ạ sẵn giải thích giùm em luôn ạ . Giải nhanh giúp em. Em cảm ơn. 
III.
A.
1. B
2. C
3. B
4. A
5. D
B.
1. C
2. B
3. B
4. A
5. C
1 b c b a d
2 c b b a c nha
Mọi người giải giúp em đề này với ạ sẵn giải thích giùm em luôn ạ. Giải nhanh giúp em. Em cảm ơn. 
Đề dài thế này sao giải thích nhanh cho e đc
Part 1
1 C
2 B
3 D
4 C
5 B
6 A
Part 2
1 T
2 F
3 F
4 F
V
1 That old house has just been bought
2 If he doesn't take these pills, he won't be better
3 I suggest taking a train
4 Spending the weekend in the countryside is very wonderful
nhiều thật đấy
Mọi người giải giúp em với sẵn giải thích giùm em luôn ạ. Giải nhanh giúp em. Em cảm ơn. 
II
1 B
2 A
3 A
4 D
5 B
6 B
7 A
8 D
9 D
10 D
Mọi người giải giúp em với sẵn giải thích giùm em luôn ạ. Giải nhanh giúp em. Em cảm ơn. 
1 B
2 C
3 A
4 D
5 D
6 B
7 D
8 C
9 A
10 B
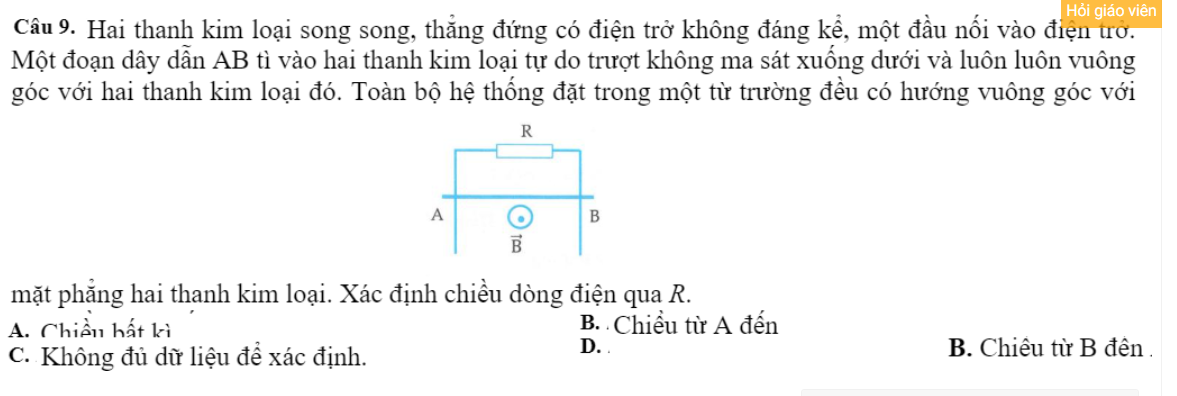
mọi người giúp em làm và giải thích câu này với ạ, em cám ơn nhiều ạ!

mọi người giúp em với ạ, e cần giải thích của câu này ạ

Lời giải:
$\frac{x-2y}{3z}$ có thể nhận giá trị lớn nhất nếu $x$ lớn nhất và $y,z$ nhỏ nhất có thể.
$x$ lớn nhất có thể nhận là $14$ (theo điều kiện)
$y,z$ nhỏ nhất có thể nhận là $1,2$ (do $y,z$ phân biệt)
Nếu $x=14, y=1,z=2$ thì $\frac{x-2y}{3z}=2$
Nếu $x=14; y=2, z=1$ thì $\frac{x-2y}{3z}=\frac{10}{3}>2$
Đáp án D.
Mọi người giải giúp em 2 câu này với ạ
3 tạ15 kg=.....................kg
Điền dấu >,<,=vào chỗ chấm sao cho thích hợp
4,3...............4,27
giải giúp em với ạ
Mọi người giải giúp em 2 câu này với ạ
3 tạ15 kg=..........315...........kg
Điền dấu >,<,=vào chỗ chấm sao cho thích hợp
4,3.......>........4,27

Mọi người giải giúp em với ạ, mai em thi rồi, mấy anh/chị giải thích rõ ràng giùm em nhé, em cảm ơn ạ.
Bài `13`
\(a,\sqrt{27}+\sqrt{48}-\sqrt{108}-\sqrt{12}\\ =\sqrt{9\cdot3}+\sqrt{16\cdot3}-\sqrt{36\cdot3}-\sqrt{4\cdot3}\\ =3\sqrt{3}+4\sqrt{3}-6\sqrt{3}-2\sqrt{3}\\ =\left(3+4-6-2\right)\sqrt{3}\\ =-\sqrt{3}\\ b,\left(\sqrt{28}+\sqrt{12}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{84}\\ =\left(\sqrt{4\cdot7}+\sqrt{4\cdot3}-\sqrt{7}\right)\cdot\sqrt{7}+\sqrt{4\cdot21}\\ =\left(2\sqrt{7}+2\sqrt{3}-\sqrt{7}\right)\cdot\sqrt{7}+2\sqrt{21}\\ =2\cdot7+2\sqrt{21}-7+2\sqrt{21}\\ =14+2\sqrt{21}-7+2\sqrt{21}\\ =7+4\sqrt{21}\)
17:
ĐKXĐ: \(\left\{{}\begin{matrix}x>=0\\x< >4\end{matrix}\right.\)
Để A là số nguyên thì \(\sqrt{x}-1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2+1⋮\sqrt{x}-2\)
=>\(\sqrt{x}-2\in\left\{1;-1\right\}\)
=>\(\sqrt{x}\in\left\{3;1\right\}\)
=>\(x\in\left\{9;1\right\}\)
16:
a: BC=BH+CH
=9+16
=25(cm)
Xét ΔABC vuông tại A có AH là đường cao
nên \(AH^2=HB\cdot HC\)
=>\(AH=\sqrt{9\cdot16}=12\left(cm\right)\)
Xét ΔABC vuông tại A có AH là đường cao
nên \(\left\{{}\begin{matrix}AB^2=BH\cdot BC\\AC^2=CH\cdot BC\end{matrix}\right.\Leftrightarrow\left\{{}\begin{matrix}AB=\sqrt{9\cdot25}=15\left(cm\right)\\AC=\sqrt{16\cdot25}=20\left(cm\right)\end{matrix}\right.\)
b: M là trung điểm của AC
=>AM=AC/2=10(cm)
Xét ΔAMB vuông tại A có
\(tanAMB=\dfrac{AB}{AM}=\dfrac{15}{10}=\dfrac{3}{2}\)
nên \(\widehat{AMB}\simeq56^0\)