Cho tam giác ABC có góc A bằng 120 độ. AB=3cm, AC=6cm.Tính độ dài đường phân giác AC.
NT
Những câu hỏi liên quan
cho tam giác abc có góc a = 120 độ ,ab=3cm,ac=6cm.tính độ dài đường phân giác ad
bài 11 ΔABC có góc BAC 12001200 ,AB6cm,AC12 cm ,phân giác góc BAC cắt BC tại D.Tính AD?bài 12 cho tam giác ABC có góc A 12001200, AB3cm,AC6cm.Tính độ dài đường phân giác AD?
Đọc tiếp
bài 11 ΔABC có góc BAC = ,AB=6cm,AC=12 cm ,phân giác góc BAC cắt BC tại D.Tính AD?
bài 12 cho tam giác ABC có góc A =, AB=3cm,AC=6cm.Tính độ dài đường phân giác AD?
11:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot6\cdot12}{6+12}\cdot\dfrac{1}{2}=4\left(cm\right)\)
12:
\(AD=\dfrac{2\cdot AB\cdot AC}{AB+AC}\cdot cos60=\dfrac{2\cdot3\cdot6}{3+6}\cdot\dfrac{1}{2}=\dfrac{3\cdot6}{3+6}=\dfrac{18}{9}=2\left(cm\right)\)
Đúng 2
Bình luận (0)
Cho tam giác abc có góc a bằng 120 độ, ab bằng 3cm, ac bằng 6cm. Tính độ dài đường phân giác ad
cho tam giác ABC có góc BAC=120 độ, AB=4cm ,AC=6cm.Tính đường phân giác AD của tam giác ABC
cho tam giác abc có góc bac=120, ab=3cm,ac=6cn.tính độ dài đường phân giác ad
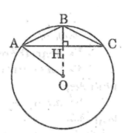
Cho tam giác cân ABC có góc B = 120 ° ,AC = 6cm.Tính độ dài đường tròn ngoại tiếp tam giác đó
Tam giác ABC có AB =AC= 3cm; góc A= 120 . Độ dài đường tròn ngoại tiếp tam giác ABC là:
\(cosA=\dfrac{AB^2+AC^2-BC^2}{2\cdot AB\cdot AC}\)
=>\(\dfrac{3^2+3^2-BC^2}{2\cdot3\cdot3}=-\dfrac{1}{2}\)
=>18-BC^2=-9
=>BC^2=27
=>\(BC=3\sqrt{3}\left(cm\right)\)
\(\dfrac{BC}{sinA}=2R\)
=>\(2\cdot R=3\sqrt{3}:sin120=3\sqrt{3}:\dfrac{1}{2}=6\sqrt{3}\)
=>\(R=3\sqrt{3}\)
Đúng 1
Bình luận (0)
Giải giùm mk vs ạ...<3! Tối nay thầy kiểm tra rồi....><!Mình cần gấp gấp gấp lắm ạ...><!
Bài 1:Cho hình bình hành ABCD,điểm G trên cạnh CD sao cho DG=2GC.Gọi E là giao điểm của AG và BD.Tính DE/EB.
Bài 2:Cho tam giác ABC có góc A=120 độ,AB=3cm,AC=6cm.Tính độ dài phân giác AD.
Bài 3:Cho tam giác ABC, AB=2cm,AC=3cm.Phân giác AD=1,2cm.Tính góc BAC.
Cho tam giác ABC có góc B bằng 120 ° , BC = 12cm, AB = 6cm. Đường phân giác của góc B cắt cạnh AC tại D. Tính độ dài đường phân giác BD
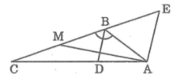

Suy ra tam giác ABE đều ⇒ AB = BE = EA = 6 (cm) (1)
Khi đó: CE = BC + BE = 12 + 6 = 18 (cm)
Tam giác ACE có AE // BD nên suy ra:
![]()
Đúng 0
Bình luận (0)