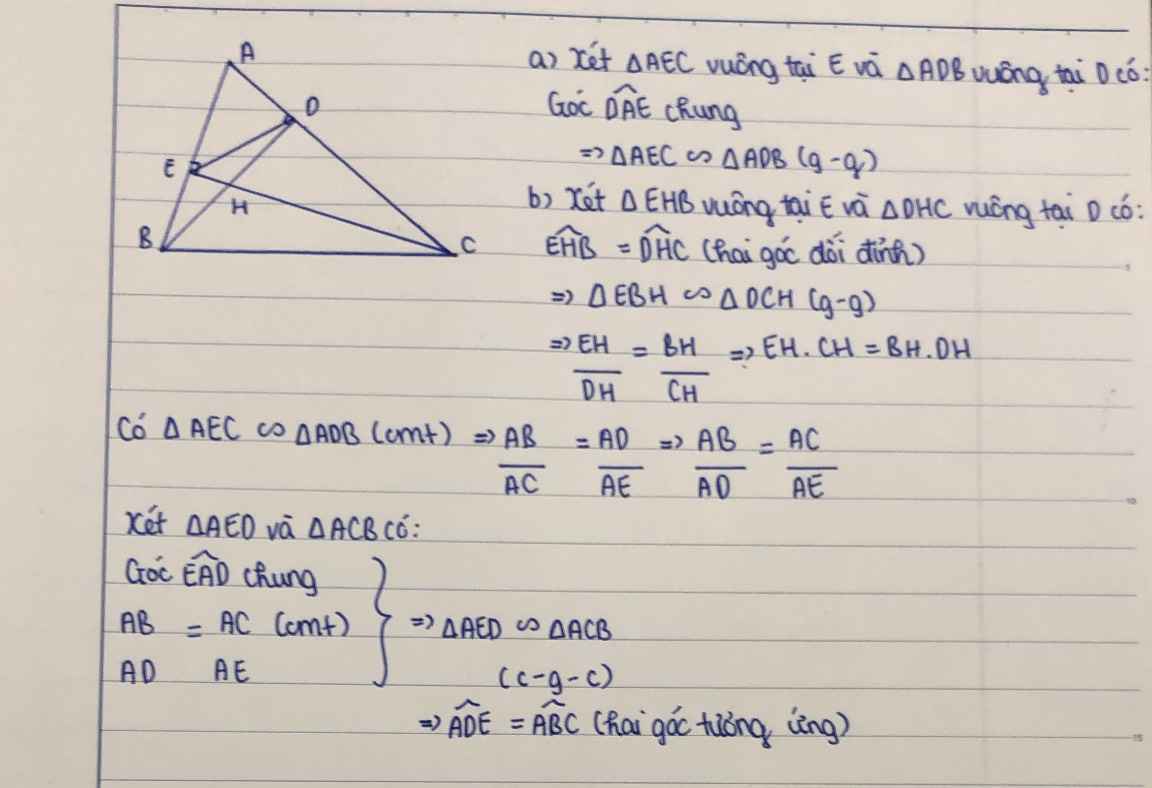Cho tam giác ABC nhọn , hai đường cao CE , BD . Chứng minh góc ADE = góc ABC
ND
Những câu hỏi liên quan
Cho tam giác ABC nhọn, các đường cao BD và CE. Chứng minh góc ABC = góc ADE cắt đường cao BD và CE Bạn nào giải nhanh giúp mk với nha, mk đang gấp
Cho tam giác ABC ccas góc đều nhọn. Các đường cao BD và CE cắt nhau tại A
a) Chứng minh tam giác ABD đồng dạng tam giác ABE
b) Chứng minh HBHD=HC x HE, góc ADE=góc ABC
a, Xét Δ ABD và Δ ABE, có :
\(\widehat{ADB}=\widehat{AEB}=90^o\)
\(\widehat{BAD}=\widehat{BAE}\) (góc chung)
=> Δ ABD ∾ Δ ABE (g.g)
b, Xét Δ EHB và Δ DHC, có :
\(\widehat{EHB}=\widehat{DHC}\) (đối đỉnh)
\(\widehat{HEB}=\widehat{HDC}=90^o\)
=> Δ EHB ∾ Δ DHC (g.g)
=> \(\dfrac{EH}{DH}=\dfrac{HB}{HC}\)
=> \(HB.HD=HC.HE\)
Đúng 1
Bình luận (0)
cho tam giác ABC có ba góc nhọn,hai đường cao BD và CE của tam giác cắt nhau tại H (D€AC,E€AB ).Chứng minh rằng:
a) chứng minh 🔺ABC đồng dạng với tam giác AEC
b) chứng minh góc ADE= góc ABC
c) kẻ HK vuông góc BC (K€BC) .chứng minh BH.BD+CH.CE=BC mũ2
vẽ hình dùm lun nha mụi ngừi cảm ơn rất nhìu
a: Xét ΔABD vuông tại D và ΔACE vuông tại E có
góc BAD chung
=>ΔABD đồng dạng với ΔACE
b: ΔABD đồng dạng với ΔACE
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC
Đúng 0
Bình luận (0)
cho tam giác ABC có ba góc nhọn,hai đường cao BD và CE của tam giác cắt nhau tại H (D€AC,E€AB ).Chứng minh rằng:
a) chứng minh 🔺ABC đồng dạng với tam giác AEC
b) chứng minh góc ADE= góc ABC
c) kẻ HK vuông góc BC (K€BC) .chứng minh BH.BD+CH.CE=BC mũ2
vẽ hình dùm lun nha mụi ngừi cảm ơn rất nhìu
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
b: góc BEC=góc BDC=90 độ
=>BEDC nội tiếp
=>góc ADE=góc ABC
Đúng 0
Bình luận (0)
Cho tam giác ABC nhọn(AB<AC), vẽ hai đường cao BD và CE cắt nhau tại H.
a) Chứng minh: Tam giác ABD đồng dạng với tam giác ACE
b)Chứng minh: góc ADE=góc ABC
c) Gọi K là giao điểm của AH và BC. CHứng minh : BD là tia phân giác của góc EDK
d) Chứng minh: BH.BD vuông góc CH.CE=BC.BC
Cho tam giác ABC có ba góc nhọn, các đường cao BD và CE ( D ∈ AC, E ∈ AB )
a) Chứng minh ΔADB đồng dạng với ΔAEC
b) Gọi H là trực tâm của ΔABC, Chứng minh HE.HC=HD.HB
c) Chứng minh góc ADE bằng góc ABC
a: Xét ΔADB vuông tại D và ΔAEC vuông tại E có
góc A chung
=>ΔADB đồng dạng với ΔAEC
b: Xet ΔHEB vuôg tại E và ΔHDC vuông tại D có
góc EHB=góc DHC
=>ΔHEB đồng dạng với ΔHDC
=>HE/HD=HB/HC
=>HE*HC=HB*HD
c: ΔADB đồng dạng với ΔAEC
=>AD/AE=AB/AC
=>AD/AB=AE/AC
=>ΔADE đồng dạng với ΔABC
=>góc ADE=góc ABC
Đúng 1
Bình luận (2)
cho tam giác ABC nhọn các đường cao BD và CE cắt nhau tại H
1 chứng minh tam giác ABC ffongf dạng với tam giác ACE và AB.AE=AC.AD
2 chứng minh góc ADE \ góc ABC
3 trên các đoạn thẳng BD và CE lấy lần lượt hai điểm M và N sao cho góc AMC = goác ANB = 90 đọ . Chứng minh AM2 = AC,AD và AM \ AN
Cho tam giác nhọn ABC có góc A bằng 60 độ, các đường cao BD và CE. Chứng minh rằng: SADE=1/4SABC
\(\Delta ACE\)vuông tại A có \(\widehat{A}=60^o\)nên \(\widehat{ACE}=30^o\)
\(\Rightarrow\frac{AE}{AC}=\frac{1}{2}\)
Tương tự : \(\frac{AD}{AB}=\frac{1}{2}\)
\(\Rightarrow\frac{AE}{AC}=\frac{AD}{AB}\Rightarrow\frac{AE}{AD}=\frac{AC}{AB}\)
chứng minh : \(\Delta ADE\approx\Delta ABC\)( c.g.c )
\(\Rightarrow\frac{S_{ADE}}{S_{ABC}}=\left(\frac{AD}{AB}\right)^2=\frac{1}{4}\)
\(\Rightarrow S_{ADE}=\frac{1}{4}S_{ABC}\)
Đúng 0
Bình luận (0)
Cho tam giác ABC có 3 góc nhọn, các đường cao BD và CE. CMR góc ADE=góc ABC
Tam giác ADE và tg ABC có
\(\hept{\begin{cases}\widehat{A}chung\\\\\frac{AD}{AE}=\frac{AB}{AC}\left(\frac{AD}{AB}=\cos\widehat{A}=\frac{AE}{AC}\right)\end{cases}}\)
Suy ra ADE đồng dạng ABC
=> đpcm
Đúng 0
Bình luận (0)