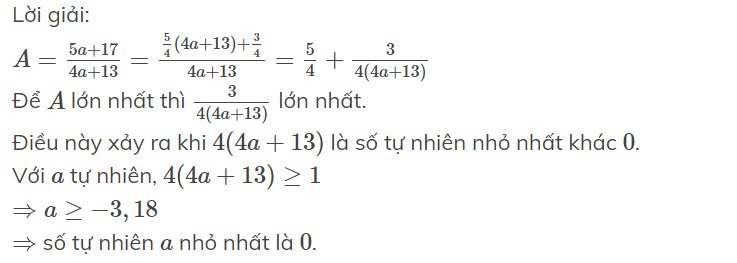với giá trị nào của số tự nhiên a thì: A = 5a-17/4a-23 có giá trị lớn nhất
HV
Những câu hỏi liên quan
Với giá trị nào của số tự nhiên a thì:
a. 8a + 19/4a +1 có giá trị nguyên.
b. 5a - 17/4a - 23 có giá trị lớn nhất.
a: Để 8a+19/4a+1 là số nguyên thì \(8a+2+17⋮4a+1\)
\(\Leftrightarrow4a+1\inƯ\left(17\right)\)
\(\Leftrightarrow4a+1\in\left\{1;-1;17;-17\right\}\)
hay \(a\in\left\{0;4\right\}\)
b: Tham khảo:
Đúng 0
Bình luận (0)
Để 8a+194a+14a+18a+19 có giá trị là số nguyên thì 8a+19⋮4a+18a+19⋮4a+1
Ta có:
8a+19⋮4a+18a+19⋮4a+1
⇒(8a+2)+17⋮4a+1⇒(8a+2)+17⋮4a+1
⇒2(4a+1)+17⋮4a+1⇒2(4a+1)+17⋮4a+1
⇒17⋮4a+1⇒17⋮4a+1
⇒4a+1∈{±1;±17}⇒4a+1∈{±1;±17}
+) 4a+1=1⇒a=04a+1=1⇒a=0 ( thỏa mãn )
+) 4a+1=−1⇒a=−124a+1=−1⇒a=2−1 ( không thỏa mãn )
+) 4a+1=17⇒a=44a+1=17⇒a=4 ( thỏa mãn )
+) 4a+1=−17⇒a=−924a+1=−17⇒a=2−9 ( không thỏa mãn )
Vậy a = 0 hoặc a = 4
b) Giải:
Để 5a−174a−234a−235a−17 có giá trị lớn nhất thì 5a−17⋮4a−235a−17⋮4a−23
Ta có:
5a−17⋮4a−235a−17⋮4a−23
⇒4(5a−17)⋮4a−23⇒4(5a−17)⋮4a−23
⇒20a−68⋮4a−23⇒20a−68⋮4a−23
⇒(20a−115)+47⋮4a−23⇒(20a−115)+47⋮4a−23
⇒5(4a−23)+47⋮4a−23⇒5(4a−23)+47⋮4a−23
⇒47⋮4a−23⇒47⋮4a−23
⇒4a−23∈{±1;±47}⇒4a−23∈{±1;±47}
+) 4a−23=1⇒a=64a−23=1⇒a=6 ( thỏa mãn )
+) 4a−23=−1⇒a=1124a−23=−1⇒a=211 ( không thỏa mãn )
+) 4a−23=47⇒a=3524a−23=47⇒a=235 ( không thỏa mãn )
+) 4a−23=−47⇒a=−64a−23=−47⇒a=−6 ( thỏa mãn )
Vì a có giá trị lớn nhất để 5a−174a−234a−235a−17 có giá trị lớn nhất nên a = 6
Vậy a = 6
Đúng 0
Bình luận (0)
Với giá trị nào của số tự nhiên a thì:
a. 8a + 19/4a + 1 có giá trị nguyên
b. 5a - 17/4a - 23 có giá trị lớn nhất
Giải:
Để \(\frac{8a+19}{4a+1}\) có giá trị là số nguyên thì \(8a+19⋮4a+1\)
Ta có:
\(8a+19⋮4a+1\)
\(\Rightarrow\left(8a+2\right)+17⋮4a+1\)
\(\Rightarrow2\left(4a+1\right)+17⋮4a+1\)
\(\Rightarrow17⋮4a+1\)
\(\Rightarrow4a+1\in\left\{\pm1;\pm17\right\}\)
+) \(4a+1=1\Rightarrow a=0\) ( thỏa mãn )
+) \(4a+1=-1\Rightarrow a=\frac{-1}{2}\) ( không thỏa mãn )
+) \(4a+1=17\Rightarrow a=4\) ( thỏa mãn )
+) \(4a+1=-17\Rightarrow a=\frac{-9}{2}\) ( không thỏa mãn )
Vậy a = 0 hoặc a = 4
b) Giải:
Để \(\frac{5a-17}{4a-23}\) có giá trị lớn nhất thì \(5a-17⋮4a-23\)
Ta có:
\(5a-17⋮4a-23\)
\(\Rightarrow4\left(5a-17\right)⋮4a-23\)
\(\Rightarrow20a-68⋮4a-23\)
\(\Rightarrow\left(20a-115\right)+47⋮4a-23\)
\(\Rightarrow5\left(4a-23\right)+47⋮4a-23\)
\(\Rightarrow47⋮4a-23\)
\(\Rightarrow4a-23\in\left\{\pm1;\pm47\right\}\)
+) \(4a-23=1\Rightarrow a=6\) ( thỏa mãn )
+) \(4a-23=-1\Rightarrow a=\frac{11}{2}\) ( không thỏa mãn )
+) \(4a-23=47\Rightarrow a=\frac{35}{2}\) ( không thỏa mãn )
+) \(4a-23=-47\Rightarrow a=-6\) ( thỏa mãn )
Vì a có giá trị lớn nhất để \(\frac{5a-17}{4a-23}\) có giá trị lớn nhất nên a = 6
Vậy a = 6
Đúng 1
Bình luận (0)
Với giá trị nào của số tự nhiên a thì (5a+17)/(4a+13) có giá trị lớn nhất ?
Lời giải:
$\frac{5a+17}{4a+13}=\frac{\frac{5}{4}(4a+13)+\frac{3}{4}}{4a+13}$
$=\frac{5}{4}+\frac{3}{4(4a+13)}$
Để phân số trên max thì $\frac{3}{4(4a+13)}$ max
Điều này xảy ra khi $4a+13$ là số nguyên dương nhỏ nhất.
Với $a$ là stn, $4a+13$ là số nguyên dương nhỏ nhất khi $a$ nhỏ nhất, bằng $0$
Vậy $a=0$
Đúng 0
Bình luận (0)
Với giá trị nào của số tự nhiên a thì:
a)a+19/4a+1 có giá trị nguyên
b)5a-17/4a-23 có giá trị lớn nhất
câu a)mình ghi thiếu phải là 8a+19
8a+19/4a+1 có giá trị nguyên thì 8a+19 chia hết cho 4a+1
=> 2(4a+1)+17 chia hết 4a+1
mà 2(4a+1) chia hết 4a+1
=> 17 chia hết 4a+1
=> 4a+1 thuộc ước của 17
=> ...............
a/ Để \(\frac{8a+19}{4a+1}\)có giá trị là số nguyên thì:
\(8a+19⋮4a+1\)
\(\Rightarrow2\left(4a+1\right)+17⋮4a+1\)
\(\Rightarrow17⋮4a+1\)
Vì \(a\in N\Rightarrow4a+1\inƯ\left(17\right)=\left\{\mp1;\mp17\right\}\)
Ta có bảng sau:
| 4a+1 | 1 | -1 | 17 | -17 |
| a | 0 | -1/2 | 4 | -9/2 |
Vì \(a\in N\Rightarrow a\in\left\{0;4\right\}\)
Xem thêm câu trả lời
Với giá trị nào của số tự nhiên a thì \(\frac{5a-17}{4a-23}\)có giá trị lớn nhất có thể?
ta co de 5a-17/4a-23 lon nhat thi mau phai nho nhat => 4a-23=1 vi khong chia duoc cho so 0 khi do 4a=24 vay a=6
Đúng 0
Bình luận (0)
Với giá trị nào của số tự nhiên a thì biểu thức: P=5a+17/4a+13 có giá trị lớn nhất
Với giá trị nào của số tự nhiên a thì phân số (5a+17)/(4a+13) có giá trị lớn nhất, giá trị đó là bao nhiêu?
Với giá trị nào của số tự nhiên a thì 5a +17 trên 4a+13 có giá trị lớn nhất và đó là mấy
Lời giải:
\(A=\frac{5a+17}{4a+13}=\frac{\frac{5}{4}(4a+13)+\frac{3}{4}}{4a+13}=\frac{5}{4}+\frac{3}{4(4a+13)}\)
Để $A$ lớn nhất thì $\frac{3}{4(4a+13)}$ lớn nhất.
Điều này xảy ra khi $4(4a+13)$ là số tự nhiên nhỏ nhất khác $0$.
Với $a$ tự nhiên, $4(4a+13)\geq 1$
$\Rightarrow a\geq -3,18$
$\Rightarrow$ số tự nhiên $a$ nhỏ nhất là $0$.
Đúng 0
Bình luận (0)
Với giá trị nào của số tự nhiên a thì:
\(\frac {5a-17}{4a-23}\) có giá trị lớn nhất