\(\text{Câu 1: Cho đường tròn (O;R) và đoạn thẳng AB cố định nằm bên ngoài đường tròn (O). Gọi C là một điểm chuyển động trên đường tròn. Tìm tập hợp các trọng tâm G của tam giác ABC.}\)
TH
Những câu hỏi liên quan
Phần tự luận
Nội dung câu hỏi 1
Cho đường tròn (O), đường kính AB, điểm C nằm giữa A và O. Vẽ đường tròn (O') có đường kính CB
a) Hai đường tròn (O) và (O') có vị trí tương đối như thế nào?
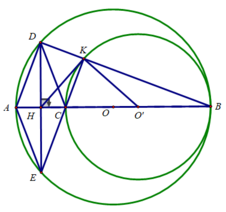
a) Ta có: OO' = OB – O'B
⇒ Hai đường tròn (O) và (O') tiếp xúc trong tại B
Đúng 0
Bình luận (0)
Cho đường tròn $O$ đường kính $AB$ và dây cung $AC$. Chứng tỏ rằng $\text{sđ } \widehat{BAC}=\frac{1}{2} \text{sđ } \overgroup{BC}$.
Xét tam giascOAC cân tại O nên ta có góc \(\widehat{CAO}=\widehat{ACO}\)
mà ta có \(sd \widebat{BC}=\widehat{BOC}=\widehat{OCA}+\widehat{CAO}=2\widehat{CAO}=2\widehat{CAB}\)
vajay ta cos dpcm
vì góc ACB chắn nửa đường tròn (O)
=> góc ACB = 90 độ mà O là trung điểm của AB
nên OC = 1/2 AB => OC=OB=OA=1/2AB
=> tam giác AOC cân tại O => góc OAC = góc OCA
Ta có góc COB = góc COA+góc OAC ( góc ngoài)
=> sđ cung BC = 2 góc CAO ( vì góc OAC=góc OCA)
=> 1/2 sđ cung BC = góc CAB
Xem thêm câu trả lời
Bài 1: Giải phương trình: sqrt{x^2text{+}12}text{+}5text{}3xtext{+}sqrt{x^2text{+}5}Bài 2: Cho đường tròn tâm O và đường tròn tâm O cắt nhau tại hai điểm phân biệt A và B (O và O nằm hác phía đối với đường thẳng AB, widehat{OAO}90) AB cắt OO tại I, OB cắt đường tròn (O) tại điểm thứ hai là C, OB cắt đường tròn (O) tại điểm thứ hai là D, AC cắt OO tại E, AD cắt OO tại Fa) CM: OO vuông góc với AB và I là trung điểm của ABb) CM: AB là tia phân giác của widehat{text{C}AD}và AEBF là hình thoic) CM: f...
Đọc tiếp
Bài 1: Giải phương trình: \(\sqrt{x^2\text{+}12}\text{+}5\text{=}3x\text{+}\sqrt{x^2\text{+}5}\)
Bài 2: Cho đường tròn tâm O và đường tròn tâm O' cắt nhau tại hai điểm phân biệt A và B (O và O' nằm hác phía đối với đường thẳng AB, \(\widehat{OAO'}\)90) AB cắt OO' tại I, O'B cắt đường tròn (O) tại điểm thứ hai là C, OB cắt đường tròn (O') tại điểm thứ hai là D, AC cắt OO' tại E, AD cắt OO' tại F
a) CM: OO' vuông góc với AB và I là trung điểm của AB
b) CM: AB là tia phân giác của \(\widehat{\text{C}AD}\)và AEBF là hình thoi
c) CM: \(\frac{OO'}{EF}\text{+}\frac{OB}{BD}\text{+}\frac{O'B}{B\text{C}}\text{=}1\)
Câu 1: Cho đường tròn (O), dây AB 48cm và cách tâm 7cm. Gọi I là trung điểm của AB, tia IO cắt đường tròn tại C. Tính khoảng cách từ O đến BC.Câu 2: Cho một đường tròn (O) và một điểm P bên trong đường tròn. Nêu cách dựng dây cung AB đi qua P để PAPB.Câu 3: Cho đường tròn (O;5) và một dây cung AB dài 6cm. Gọi I là trung điểm của AB. Tia OI cắt cung Ab tại M. Tính độ dài dây cung MA.
Đọc tiếp
Câu 1: Cho đường tròn (O), dây AB = 48cm và cách tâm 7cm. Gọi I là trung điểm của AB, tia IO cắt đường tròn tại C. Tính khoảng cách từ O đến BC.
Câu 2: Cho một đường tròn (O) và một điểm P bên trong đường tròn. Nêu cách dựng dây cung AB đi qua P để PA=PB.
Câu 3: Cho đường tròn (O;5) và một dây cung AB dài 6cm. Gọi I là trung điểm của AB. Tia OI cắt cung Ab tại M. Tính độ dài dây cung MA.
Câu 1: Cho đường tròn (O), dây AB 48cm và cách tâm 7cm. Gọi I là trung điểm của AB, tia IO cắt đường tròn tại C. Tính khoảng cách từ O đến BC.Câu 2: Cho một đường tròn (O) và một điểm P bên trong đường tròn. Nêu cách dựng dây cung AB đi qua P để PAPB.Câu 3: Cho đường tròn (O;5) và một dây cung AB dài 6cm. Gọi I là trung điểm của AB. Tia OI cắt cung Ab tại M. Tính độ dài dây cung MA.Giúp mình với mình cần gấp huhu :
Đọc tiếp
Câu 1: Cho đường tròn (O), dây AB = 48cm và cách tâm 7cm. Gọi I là trung điểm của AB, tia IO cắt đường tròn tại C. Tính khoảng cách từ O đến BC.
Câu 2: Cho một đường tròn (O) và một điểm P bên trong đường tròn. Nêu cách dựng dây cung AB đi qua P để PA=PB.
Câu 3: Cho đường tròn (O;5) và một dây cung AB dài 6cm. Gọi I là trung điểm của AB. Tia OI cắt cung Ab tại M. Tính độ dài dây cung MA.
Giúp mình với mình cần gấp huhu :<
bộ định bảo mọi người làm hết bài tập cho à
Đúng 0
Bình luận (1)
Giúp mừn với :Câu 1: Cho đường tròn (O), dây AB 48cm và cách tâm 7cm. Gọi I là trung điểm của AB, tia IO cắt đường tròn tại C. Tính khoảng cách từ O đến BC.Câu 2: Cho một đường tròn (O) và một điểm P bên trong đường tròn. Nêu cách dựng dây cung AB đi qua P để PAPB.Câu 3: Cho đường tròn (O;5) và một dây cung AB dài 6cm. Gọi I là trung điểm của AB. Tia OI cắt cung Ab tại M. Tính độ dài dây cung MA.
Đọc tiếp
Giúp mừn với :<<
Câu 1: Cho đường tròn (O), dây AB = 48cm và cách tâm 7cm. Gọi I là trung điểm của AB, tia IO cắt đường tròn tại C. Tính khoảng cách từ O đến BC.
Câu 2: Cho một đường tròn (O) và một điểm P bên trong đường tròn. Nêu cách dựng dây cung AB đi qua P để PA=PB.
Câu 3: Cho đường tròn (O;5) và một dây cung AB dài 6cm. Gọi I là trung điểm của AB. Tia OI cắt cung Ab tại M. Tính độ dài dây cung MA.
Cho đường tròn (O; R) và điểm A sao cho OA= 3R. Vẽ đường tròn đường kính OA cắt đường tròn O tại B,C Chứng minh AB, AC là tiếp tuyến đường tròn (O)
Câu 1 : 1) Cho đường tròn tâm O bán kính R. Từ điểm D nằm ngoài đường tròn vě hai tiếp tuyến DA và DM đến đường tròn (A và M lần lượt là các tiếp điểm). a) Chứng minh 4 điểm A, ), M, D cùng thuộc một đường tròn. b) Kể đường kính AB của (O). Tia phân giác của góc MOB cắt tia DM tại C. Chứng minh tam giác DOC là tam giác vuông.2)Một chiếc máy bay đang bay song song với mặt đất ở độ cao 15km thì bắt đầu hạ cánh, đường hạ cánh của máy bay tạo với mặt đất một góc 30°. 30 Sau khi tiếp đất, máy bay đi...
Đọc tiếp
Câu 1 :
1) Cho đường tròn tâm O bán kính R. Từ điểm D nằm ngoài đường tròn vě hai tiếp tuyến DA và DM đến đường tròn (A và M lần lượt là các tiếp điểm). a) Chứng minh 4 điểm A, ), M, D cùng thuộc một đường tròn. b) Kể đường kính AB của (O). Tia phân giác của góc MOB cắt tia DM tại C. Chứng minh tam giác DOC là tam giác vuông.
2)Một chiếc máy bay đang bay song song với mặt đất ở độ cao 15km thì bắt đầu hạ cánh, đường hạ cánh của máy bay tạo với mặt đất một góc 30°. 30 Sau khi tiếp đất, máy bay đi thẳng với vận tốc trung bình là 21km/h để đến điểm trả ách. Tính thời gian từ lúc máy bay tiếp đất đến khi máy bay dừng tại điểm trả khách, biết ang đường từ điểm bắt đầu hạ cánh đến điểm trả khách là 33,5km?
Câu 1:
1:
a: Xét tứ giác OAMD có
\(\widehat{OAM}+\widehat{ODM}=180^0\)
Do đó: OAMD là tứ giác nội tiếp
Đúng 0
Bình luận (0)
Câu 1: Cho 2 đường tròn (O;R) và (O’;r), R r Trong các phát biểu sau phát biểu nào là phát biểu saiA. Hai đường tròn (O) và (O’) cắt nhau khi và chỉ khi R - r OO R + rB. Hai đường tròn (O) và (O’) tiếp xúc ngoài khi và chỉ khi OO’ R - rC. Hai đường tròn (O) và (O’) tiếp xúc trong khi và chỉ khi OO’ R - rD. Hai đường tròn (O) và (O’) gọi là ngoài nhau khi và chỉ khi OO’ R + rCâu 2: Gọi d là khoảng cách 2 tâm của (O, R) và (O, r) với 0 r R. Để (O) và (O) tiếp xúc trong thì:A. R - r d...
Đọc tiếp
Câu 1: Cho 2 đường tròn (O;R) và (O’;r), R > r
Trong các phát biểu sau phát biểu nào là phát biểu sai
A. Hai đường tròn (O) và (O’) cắt nhau khi và chỉ khi R - r < OO' < R + r
B. Hai đường tròn (O) và (O’) tiếp xúc ngoài khi và chỉ khi OO’ = R - r
C. Hai đường tròn (O) và (O’) tiếp xúc trong khi và chỉ khi OO’ = R - r
D. Hai đường tròn (O) và (O’) gọi là ngoài nhau khi và chỉ khi OO’ > R + r
Câu 2: Gọi d là khoảng cách 2 tâm của (O, R) và (O', r) với 0 < r < R. Để (O) và (O') tiếp xúc trong thì:
A. R - r < d < R + r
B. d = R - r
C. d > R + r
D. d = R + r
Câu 3: Cho hai đường tròn tâm O và O' có d=OO' và bán kính lần lượt R và R'.Trong các câu sau,câu nào sai?
A.Điều kiện cần và đủ để hai đường tròn đã cho cắt nhau là: R-R'<d<R+R'
B.Điều kiện cần và đủ để hai đường tròn đã cho cắt nhau là: |R-R'|<d<R+R'
C.Điều kiện cần và đủ để hai đường tròn đã cho cắt nhau là R,R' và d là độ dài ba cạnh của một tam giác
D.Trong ba câu trên,chỉ có câu a là câu sai
Câu 4: Cho hai đường tròn đồng tâm O,bán kính R và 2R.Gọi P là một điểm nằm ngoài đường tròn (O,2R).Vé đường tròn tâm P bán kính PO,cắt đường tròn (O,2R) tại 2 điểm C,D.OC cắt đường tròn (O;R) tại E.OD cắt đường tròn (O;R) tại F.Khi đó:
(1) EO=EC=R và OF=FD=R
(2) PE là đường cao của tam giác POC
(3) PF là đường cao của tam giác POD
Trong các câu trên:
A.Chỉ có câu (1) đúng
B.Chỉ có câu (2) đúng
C.Chỉ có câu (3) đúng
D.Cả ba câu đều đúng
E.Tất cả ba câu đều sai
Câu 5: Cho đường tròn (O). A, B, C là 3 điểm thuộc đường tròn sao cho tam giác ABC cân tại A. Phát biểu nào sau đây đúng
Tiếp tuyến của đường tròn tại A là
A. Đi qua A và vuông góc AB
B. Đi qua A và song song BC
C. Đi qua A và song song AC
D. Đi qua A và vuông góc BC


