Tính giá trị nhỏ nhất của biểu thức: A= \(8x^2+3y^2-8xy-6y=21\)
NC
Những câu hỏi liên quan
tìm giá trị nhỏ nhất của p = 8x^2 +3y^2 -8xy-6y+21
`Answer:`
\(P=8x^2+3y^2-8xy-6y+21\)
\(=\left(8x^2-8xy+2y^2\right)+y^2-6y+9+12\)
\(=2.\left(4x^2-4xy+y^2\right)+\left(y-3\right)^2+12\)
\(=2.\left(2x-y\right)^2+\left(y-3\right)^2+12\)
\(\Rightarrow P\ge2.0+0+12=12\)
Dấu "=" xảy ra khi \(\hept{\begin{cases}x=\frac{3}{2}\\y=3\end{cases}}\)
Tìm giá trị nhỏ nhất của \(P=8x^2+3y^2-8xy-6y+21\)
Ta có :
\(P=8x^2+3y^2-8xy-6y+21\)
\(=\left(8x^2-8xy+2y^2\right)+\left(y^2-6y+9\right)+12\)
\(=2\left(4x^2-4xy+y^2\right)+\left(y-3\right)^2+12\)
\(=2\left(2x-y\right)^2+\left(y-3\right)^2+12\)
Ta có
\(2\left(2x-y\right)^2+\left(y-3\right)^2\ge0\) với mọi x , y
Suy ra :
\(2\left(2x-y\right)^2+\left(y-3\right)^2+12\ge12\)
\(\Leftrightarrow P\ge12\)
Dấu " = " xảy ra khi \(2x-y=y-3=0\) . Suy ra \(x=\frac{3}{2},y=3\)
Vậy GTNN của P là 12, đạt được khi \(x=\frac{3}{2},y=3\)
giá trị nhỏ nhất của biểu thức 2x^2+2y^2-2xy-6y+21
tìm x,y để biểu thức B đạt giá trị nhỏ nhất, timg giá trị nhỏ nhất:
B=x^4 - 8xy - x^3y + x^2y^2 - xy^3 + y^4 + 2015
b1. Tìm giá trị nhỏ nhất của biểu thức sau:
a) A=x^2-10x+12
b)B=6y^2+4y-1
c)C=x^2+y^2-2x-6y-1
d)D=2x62+3y^2-x-3y+5
A = x2 - 10x + 12
= ( x2 - 10x + 25 ) - 13
= ( x - 5 )2 - 13
( x - 5 )2 ≥ 0 ∀ x => ( x - 5 )2 - 13 ≥ -13
Đẳng thức xảy ra <=> x - 5 = 0 => x = 5
=> MinA = -13 <=> x = 5
B = 6y2 + 4y - 1
= 6( y2 + 2/3y + 1/9 ) - 5/3
= 6( y + 1/3 )2 - 5/3
6( y + 1/3 )2 ≥ 0 ∀ x => 6( y + 1/3 )2 - 5/3 ≥ -5/3
Đẳng thức xảy ra <=> y + 1/3 = 0 => y = -1/3
=> MinB = -5/3 <=> y = -1/3
C = x2 + y2 - 2x - 6y - 1
= ( x2 - 2x + 1 ) + ( y2 - 6y + 9 ) - 11
= ( x - 1 )2 + ( y - 3 )2 - 11
\(\hept{\begin{cases}\left(x-1\right)^2\ge0\forall x\\\left(y-3\right)^2\ge0\forall y\end{cases}\Rightarrow}\left(x-1\right)^2+\left(y-3\right)^2-11\ge-11\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x-1=0\\y-3=0\end{cases}}\Rightarrow\hept{\begin{cases}x=1\\y=3\end{cases}}\)
=> MinC = -11 <=> x = 1 ; y = 3
D = 2x2 + 3y2 - x - 3y + 5
= 2( x2 - 1/2x + 1/16 ) + 3( y2 - y + 1/4 ) + 33/8
= 2( x - 1/4 )2 + 3( y - 1/2 )2 + 33/8
\(\hept{\begin{cases}2\left(x-\frac{1}{4}\right)^2\ge0\forall x\\3\left(y-\frac{1}{2}\right)^2\ge0\forall y\end{cases}}\Rightarrow2\left(x-\frac{1}{4}\right)^2+3\left(y-\frac{1}{2}\right)^2+\frac{33}{8}\ge\frac{33}{8}\)
Đẳng thức xảy ra <=> \(\hept{\begin{cases}x-\frac{1}{4}=0\\y-\frac{1}{2}=0\end{cases}}\Rightarrow\hept{\begin{cases}x=\frac{1}{4}\\y=\frac{1}{2}\end{cases}}\)
=> MinD = 33/8 <=> x = 1/4 ; y = 1/2
Cho
z
x
+
y
i
x
,
y
∈
R
là số phức thỏa mãn điều kiện
z
¯
+
2...
Đọc tiếp
Cho z = x + y i x , y ∈ R là số phức thỏa mãn điều kiện z ¯ + 2 - 3 i ≤ z + i - 2 ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 y . Tính M + m
A. 156 5 - 20 10
B. 60 - 20 10
C. 156 5 + 20 10
D. 60 + 20 10
Chọn đáp án B

Từ giả thiết ta có:
![]()
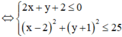
Suy ra tập hợp các điểm biểu diễn số phức z là miền mặt phẳng
(T) thỏa mãn 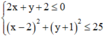 (miền tô đậm trong hình vẽ bên
(miền tô đậm trong hình vẽ bên
Gọi A, B là các giao điểm của đường thẳng 2 x + y + 2 = 0 và đường tròn (C’) : x - 2 2 + y + 1 2 = 25
Ta tìm được A(2; -6) và B(-2; 2)
Ta có :
![]()
![]()
Đường tròn (C) cắt miền (T) khi và chỉ khi
![]()
![]()
![]()
Đúng 0
Bình luận (0)
Bài 3:
a, Tính giá trị của biểu thức A = \(5xy-10+3y\) tại \(x=2\) và \(y=-3\)
b, Tính giá trị của biểu thức B = \(8xy^2-xy-2x-10\) tại \(x=1\) và \(y=-1\)
a: \(A=5\cdot2\cdot\left(-3\right)-10+3\cdot\left(-3\right)=-30-10-9=-49\)
b: \(B=8\cdot1\cdot\left(-1\right)^2-1\cdot\left(-1\right)-2\cdot1-10\)
=8+1-2-10
=-3
Đúng 4
Bình luận (0)
a: A=5⋅2⋅(−3)−10+3⋅(−3)=−30−10−9=−49
b: B=8⋅1⋅(−1)2−1⋅(−1)−2⋅1−10
=8+1-2-10
=-3
Đúng 0
Bình luận (0)
Tìm giá trị nhỏ nhất của các biểu thức:
\(A=5x^2+13y^2+8xy-8x-12y+4\)
\(B=\frac{x^2+1}{x^2-x+1}\)
Bài giải
\(B=\frac{x^2+1}{x^2-x+1}=\frac{x^2+1-x+x}{x^2-x+1}=\frac{x^2+1-x}{x^2-x+1}+\frac{x}{x^2-x+1}=1+\frac{x}{x^2-x+1}\)
\(B\) nhỏ nhất khi \(\frac{x}{x^2-x+1}\) nhỏ nhất
\(\Leftrightarrow\text{ }x\text{ nhỏ nhất}\text{ }\Rightarrow\text{ }x=0\)
Thay \(x=0\) ta có :
\(B=\frac{x^2+1}{x^2-x+1}=\frac{0^2+1}{0^2-0+1}=\frac{1}{1}=1\)
Vậy \(GTNN\) của \(B=1\)
Đúng 0
Bình luận (0)
Cho zx+yi với
x
,
y
∈
ℝ
là số phức thỏa mãn điều kiện
z
→
+
2
-
3
i
≤
z
+
i
-
2
≤
5
. Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu...
Đọc tiếp
Cho z=x+yi với x , y ∈ ℝ là số phức thỏa mãn điều kiện z → + 2 - 3 i ≤ z + i - 2 ≤ 5 . Gọi M, m lần lượt là giá trị lớn nhất và giá trị nhỏ nhất của biểu thức P = x 2 + y 2 + 8 x + 6 y . Tính M+m.
A. 60 + 2 10
B. 156 6 - 20 10 .
C. 60 - 2 10 .
D. 156 5 + 20 10







