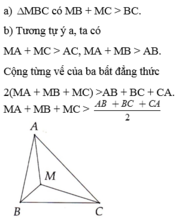
cho tma giác ABC . gọi M là một điểm bất kif của tam giác đó.
CMR : MA +MB +MC > 1/2 (AB + AC + BC)
TB
Những câu hỏi liên quan
1 ) Cho tam giác ABC . Gọi M là một điểm nằm trong tam giác . Chứng minh rằng : MA + MB + MC > nửa chu vi tam giác đó
2 ) Cho tam giác ABC . Gọi M là trung điểm cạnh BC . Chứng minh rằng : AM < AB + AC / 2
Cho tam giác ABC, điểm M bất kì nằm trong tam giác.a) So sánh MB + MC với BC.b) Chứng minh 2(MA + MB + MC) AB + BC + CA.c) Gọi I là giao điểm của đường thẳng BM và cạnh AC. So sánh MC và MI + IC, từ đó chứng minh MB + MC IB + ICd) So sánh IB và IA + AB, từ đó chứng minh IB + IC AB + ACe) Chứng minh MB + MC AB + ACf) Chứng minh MA + MB + MC AB + BC + AC
Đọc tiếp
Cho tam giác ABC, điểm M bất kì nằm trong tam giác.
a) So sánh MB + MC với BC.
b) Chứng minh 2(MA + MB + MC) > AB + BC + CA.
c) Gọi I là giao điểm của đường thẳng BM và cạnh AC. So sánh MC và MI + IC, từ đó chứng minh MB + MC < IB + IC
d) So sánh IB và IA + AB, từ đó chứng minh IB + IC < AB + AC
e) Chứng minh MB + MC < AB + AC
f) Chứng minh MA + MB + MC < AB + BC + AC
c)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
d)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
e)Từ (2) và (4) suy ra MB+MC<AB+AC
f)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)
Đúng 0
Bình luận (0)
a) Xét ΔBMC ta có: MB + MC > BC (bất đẳng thức tam giác)
b)
*Xét ΔABM ta có: AM + BM > AB (1)
*Xét ΔACM ta có: AM + CM > AC (2)
*Xét ΔBMC ta có: BM + CM > BC (3)
Từ (1); (2); (3)
=> AM + BM + AM + CM + BM + CM > AB + AC + BC
=> 2. AM + 2. BM + 2. CM > AB + AC + BC
=> 2. (AM + BM + CM) > AB + AC + BC
Hay: 2. (MA + MB + MC) > AB + BC + CA
Đúng 0
Bình luận (0)
Cho tam giác ABC, điểm M bất kì nằm trong tam giác.a) So sánh MB + MC với BC.b) Chứng minh 2(MA + MB + MC) AB + BC + CA.c) Gọi I là giao điểm của đường thẳng BM và cạnh AC. So sánh MC và MI + IC, từ đó chứng minh MB + MC IB + ICd) So sánh IB và IA + AB, từ đó chứng minh IB + IC AB + ACe) Chứng minh MB + MC AB + ACf) Chứng minh MA + MB + MC AB + BC + AC
Đọc tiếp
Cho tam giác ABC, điểm M bất kì nằm trong tam giác.
a) So sánh MB + MC với BC.
b) Chứng minh 2(MA + MB + MC) > AB + BC + CA.
c) Gọi I là giao điểm của đường thẳng BM và cạnh AC. So sánh MC và MI + IC, từ đó chứng minh MB + MC < IB + IC
d) So sánh IB và IA + AB, từ đó chứng minh IB + IC < AB + AC
e) Chứng minh MB + MC < AB + AC
f) Chứng minh MA + MB + MC < AB + BC + AC
a) Xét ΔBMC ta có: MB + MC > BC (bất đẳng thức tam giác)
b)
*Xét ΔABM ta có: AM + BM > AB (1)
*Xét ΔACM ta có: AM + CM > AC (2)
*Xét ΔBMC ta có: BM + CM > BC (3)
Từ (1); (2); (3)
=> AM + BM + AM + CM + BM + CM > AB + AC + BC
=> 2. AM + 2. BM + 2. CM > AB + AC + BC
=> 2. (AM + BM + CM) > AB + AC + BC
Hay: 2. (MA + MB + MC) > AB + BC + CA
c)Gọi I là giao điểm của BM và AC.
Áp dụng bất đẳng thức tam giác vào ΔIMC ta có: MC<MI+IC (1)
Cộng MB vào hai vế (1) ta được: MC+MB<MI+IC+MB
⇒MC+MB<MI+MB+IC
⇒MC+MB<IB+IC (2)
d)Áp dụng bất đẳng thức tam giác vào ΔIBA ta có: IB<IA+AB (3)
Cộng IC vào hai vế (3) ta được: IB+IC<IA+AB+IC
⇒ IB+IC<IA+IC+AB
⇒IB+IC<AC+AB (4)
e)Từ (2) và (4) suy ra MB+MC<AB+AC
f)Áp dụng bđt tam giác, ta có:
AB+AI > BI = MB+MI, CI + MI > MC
=> AB + AI + CI + MI > MB + MI + MC
Mà AI + CI = AC
=> AB + AC > MB + MC [1]
Áp dụng bđt tam giác, ta cũng có:
BA + BC > MA + MC [2],
CA + CB > MA + MB [3]
Từ [1][2][3] => 2 (AB+AC+CA) > MA + MB + MC
=> MA + MB + MC < AB + AC + BC (đpcm)
Đúng 0
Bình luận (0)
Cho điểm M nằm trong tam giác ABC. 1) So sánh AB với MA + MB . 2) CMR: AB + AC + BC < 2(MA + MB + MC) . 3) Chứng minh rằng MA + MB +MC lớn hơn nửa chu vi tam giác ABC.
a) Cho tam giác ABC , M là một điểm bất kì nằm trong tam giác . Chứng minh: 2 ( MA +MB +MC) > AB + AC + BC .
b) Cho tam giác ABC , có AN , BP , CQ là ba trung tuyến . Chứng minh : 4/3 ( AN + BP + CQ) > AB + AC + BC .
Cho tam giác đều ABC nội tiếp đường tròn tâm O bán kính R. Gọi M là một điểm bất kì thuộc cung BC.
a) Chứng minh rằng MA = MB + MC
b) Gọi D là giao điểm của MA và BC. Chứng minh rằng \(\frac{MD}{MB}+\frac{MD}{MC}=1\)
c) Tính tổng MA^2 + MB^2 MC ^2 theo R.
Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.a) So sánh MB + MC với BCb) Chứng minh
M
A
+
M
B
+
M
C
A
B
+
B
C
+
C
A
2
Đọc tiếp
Cho tam giác ABC, điểm M bất kỳ nằm trong tam giác.
a) So sánh MB + MC với BC
b) Chứng minh M A + M B + M C > A B + B C + C A 2
Cho M là một điểm nằm trong tam giác ABC. Chứng minh
1/2*(AB+BC+CA) < MA + MB + MC < AB + AC + BC
Không làm mà đòi có ăn thì ............................................
Nguôi ta de len day de giúp chu ko de cho may Súa nhe con .......
ai giúp mình với
cùng câu hỏi
Xem thêm câu trả lời
Cho tam giác ABC đều. M là 1 điểm bất kì nằm trong tam giác. Gọi A', B', C' lần lượt là hình chiếu của M lên các cạnh BC, CA, AB. CMR: a) MA' + MB' + MC' không đổi. b)AC' +BA' + MC' không đổi