Lời giải:
Chiều cao của tam giác $ABC$ ứng với đáy BC: $37,5\times 2: 5= 15$ (cm) 

Độ dài đáy BC: $150\times 2:15=20$ (cm)

  Diện tích hình vuông là :

        8 x 8 = 64 ( cm )

  Đường cao của hình tam giác là:

        64 x 2 : 10 = 12,8 ( cm )

               Đáp số : 12,8 cm

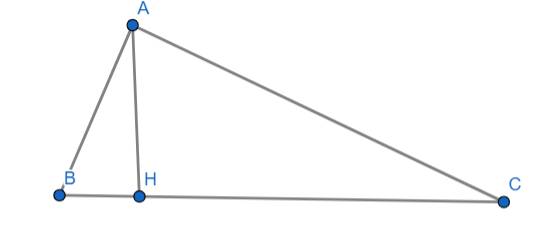
Xét tam giác vuông ABC vuông tại A có đường cao AH là:

\(AC^2=HC\cdot BC\)

\(\Rightarrow AC^2=\left(BC-HB\right)\cdot BC\)

\(\Rightarrow6^2=\left(BC-5\right)\cdot BC\)

\(\Rightarrow BC^2-5BC-36=0\)

\(\Rightarrow\left[{}\begin{matrix}BC=9\left(cm\right)\left(tm\right)\\BC=-4\left(cm\right)\left(ktm\right)\end{matrix}\right.\)

\(\Rightarrow AB=\sqrt{BC\cdot BH}=\sqrt{9\cdot5}=3\sqrt{5}\left(cm\right)\)

\(\Rightarrow AH=\dfrac{AB^2\cdot AC^2}{AB^2+AC^2}=\dfrac{6^2\cdot\left(3\sqrt{5}\right)^2}{6^2+\left(3\sqrt{5}\right)^2}=20\left(cm\right)\)

Diện tích tam giác ABC là:

\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot9\cdot20=90\left(cm^2\right)\)

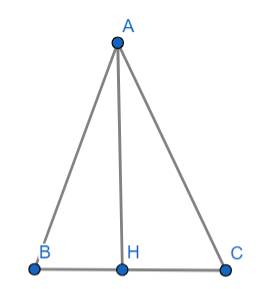
Xét tam giác vuông ABH vuông tại H ta có: 

\(AB^2=BH^2+AH^2\)

\(\Rightarrow AH=\sqrt{AB^2-BH^2}\)

\(\Rightarrow AH=\sqrt{6^2-5^2}=\sqrt{11}\left(cm\right)\)

Mà tam giác ABC cân tại A nên \(BC=2BH=2\cdot5=10\left(cm\right)\)  

Diện tích tam giác ABC là: 

\(S_{ABC}=\dfrac{1}{2}\cdot AH\cdot BC=\dfrac{1}{2}\cdot10\cdot\sqrt{11}=5\sqrt{11}\left(cm^2\right)\)

giai gap gium mik nhe cam mon nhieu lam luon

a, + △ABC vuông ở A nên theo định lí Pytago ta có: AB2+AC2=BC2
Hay: 52+AC2=132⟹AC=12

+ E là trung điểm của AB nên AE=EB=AB2=52=2,5

+ N là trung điểm của AC nên AN=CN=AC2=122=6

+ △AEC vuông ở A nên theo định lí Pytago ta có: EC2=AE2+AC2=2,52+122=150,25⟹EC≈12.3

+ △ANB vuông ở A nên theo định lí Pytago ta có: NB2=AB2+AN2=5^22+66

2=61⟹BN≈7,8

+ Trong tam giác vuông, trung tuyến ứng với cạnh huyền bằng một nửa cạnh huyền nên AM=BC2=6,5

b,+ SABC=AB.AC:2=12.5:2=30 

+ M là trung điểm BC nên BM=MC. Mà △OBM và △OCM có chung đường cao kẻ từ O nên SOBM=SOCM

+ N là trung điểm AC nên AN=NC. Mà △AON và △OCN có chung đường cao kẻ từ O nên SAON=SCON

+ E là trung điểm AB nên AE=EB. Mà △OAE và △OEB có chung đường cao kẻ từ O nên SOAE=SOEB

+ Ta có: SOBM+SOCM+SAON+SCON+SOAE+SOEB=SABC. Hay:
6.SOBM=SABC⟹SOBM=SOCM=SABC6=30:6=5 (cm2)

+Vậy SBOC=SOBM+SOCM=5.2=10 (cm2)

 

SAO TRA LOI DAI THE