Cho ΔABC và tam giác có ba đỉnh D; E; F biết AB = EF, B=F. Cần thêm điều kiện gì để hai
tam giác bằng nhau theo trường hợp góc – cạnh – góc
A. AC = FD B. A=F C. C=E D. A=E
AT
Những câu hỏi liên quan
CTV và GV ơi giúp em vs
Chứng minh rằng ΔABC đồng dạng với một tam giác có ba cạnh lần lượt bằng độ dài đường cao ứng với ba đỉnh của tam giác ABC.
Cô thầy ơi cứu em :(
Cho tam giác ABC vuông tại A có AB = 5cm, BC = 10cm.
a) Tính độ dài AC.
b) Vẽ đường phân giác BD của ΔABC và gọi E là hình chiếu của D trên BC. Chứng minh ΔABD = ΔEBD và .
c) Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh: ΔABC = ΔAFC.
d) Qua A vẽ đường thẳng song song với BC cắt CF tại G. Chứng minh ba điểm B, D, G thẳng hàng.
a: AC=căn 10^2-5^2=5*căn 3(cm)
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
góc ABD=góc EBD
=>ΔBAD=ΔBED
c: Sửa đề: ΔBEF=ΔBAC
Xét ΔBEF vuông tại E và ΔBAC vuông tại A có
BE=BA
góc FBE chung
=>ΔBEF=ΔBAC
Đúng 0
Bình luận (0)
mấy bạn giúp mik câu hỏi mik mới đăng đi,chỉ lần này thôi !
Chứng minh rằng ΔABC đồng dạng với một tam giác có ba cạnh lần lượt bằng độ dài đường cao ứng với ba đỉnh của tam giác ABC.
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...b) Nếu
Δ
A
B
C
~
Δ
D
E
F
với tỉ số đồng dạng là 1/2 và
Δ
D
E
F
~
Δ
M
N
P
với tỉ số đồng dạng là 4/3 thì
Δ
M
N
P...
Đọc tiếp
Chọn đúng (Đ), sai (S) điền vào chỗ chấm.
a) Nếu hai tam giác cân có các góc ở đỉnh bằng nhau thì đồng dạng với nhau. ...
b) Nếu Δ A B C ~ Δ D E F với tỉ số đồng dạng là 1/2 và Δ D E F ~ Δ M N P với tỉ số đồng dạng là 4/3 thì Δ M N P ~ Δ A B C với tỉ số đồng dạng là 2/3 ....
c) Trên cạnh AB, AC của ΔABC lấy 2 điểm I và K sao cho A I / A B = A K / B C t h ì I K / / B C . . . .
d) Hai tam giác đồng dạng thì bằng nhau....
Cho tam giác ABC vuông tại A có AB = 5cm, BC = 10cm.
a) Tính độ dài AC.
b) Vẽ đường phân giác BD của ΔABC và gọi E là hình chiếu của D trên BC. Chứng minh: ΔABD = ΔEBD và AE ⊥ BD.
c) Gọi giao điểm của hai đường thẳng ED và BA là F. Chứng minh: ΔABC = ΔAFC. d) Qua A vẽ đường thẳng song song với BC cắt CF tại G. Chứng minh ba điểm B, D, G thẳng hàng. làm cho mình câu c với câu d thôi ạ
a: \(AC=\sqrt{BC^2-AB^2}=5\sqrt{3}\left(cm\right)\)
b: Xét ΔABD vuông tại A và ΔEBD vuông tại E có
BD chung
\(\widehat{ABD}=\widehat{EBD}\)
Do đó: ΔABD=ΔEBD
Suy ra: BA=BE và DA=DE
=>BD là đường trung trực của AE
hay BD\(\perp\)AE
Đúng 0
Bình luận (0)
Cho hai tam giác bằng nhau: tam giác ABC và một tam giác có ba đỉnh H, K, D. Hãy viết kí hiệu sự bằng nhau của hai tam giác đó biết rằng AB = KD; ∠B =∠K
Ta có: ∠B =∠K nên đỉnh B tương ứng với đỉnh K
AB = KD nên đỉnh A tương ứng với đỉnh D
Suy ra đỉnh C tương ứng với đỉnh H
Vậy ΔABC=ΔDKH
Đúng 0
Bình luận (0)
Cho hai tam giác bằng nhau: tam giác ABC và một tam giác có ba đỉnh D,E,F. Hãy viết kí hiệu sự bằng nhau của hai tam giác đó, biết rằng: ∠A =∠F ;∠B =∠E
Vì ∠A =∠F nên đỉnh A tương ứng với đỉnh F
Vì ∠B =∠E nên đỉnh B tương ứng với đỉnh E
Suy ra đỉnh C tương ứng với đỉnh D
Vậy ΔABC=ΔFED
Đúng 0
Bình luận (0)
Cho hai tam giác bằng nhau: tam giác ABC và một tam giác có ba đỉnh D,E,F. Hãy viết kí hiệu sự bằng nhau của hai tam giác đó, biết rằng: AB=ED,AC=FD
Ta có: AB = ED và AC = FD nên đỉnh A tương ứng với đỉnh D, đỉnh B tương ứng đỉnh E, đỉnh C tương ứng với F.
Vậy ΔABC=ΔDEF
Đúng 0
Bình luận (0)
Một đa giác lồi có 10 đỉnh. Chọn ngẫu nhiên ba đỉnh của đa giác và nối chúng lại với nhau ta được một tam giác. Tính xác suất để tam giác thu được có ba cạnh là ba đường chéo của đa giác đã cho. A.
11
12
B.
1
4
C.
3
8
D.
5
12
Đọc tiếp
Một đa giác lồi có 10 đỉnh. Chọn ngẫu nhiên ba đỉnh của đa giác và nối chúng lại với nhau ta được một tam giác. Tính xác suất để tam giác thu được có ba cạnh là ba đường chéo của đa giác đã cho.
A. 11 12
B. 1 4
C. 3 8
D. 5 12
HD: Chọn ra 3 đỉnh bất kỳ của đa giác có: C 10 3 cách chọn.
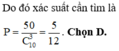
■ Số tam giác có 2 cạnh là cạnh của đa giác là: 10
(vì ứng với mỗi đỉnh ta lấy 2 cạnh kề với nó là được tgiác như điều kiện đã xét)
■ Số tam giác có 1 cạnh là cạnh của đa giác là: 10.6 = 60 vì chọn 1 cạnh của đa giác, ta chọn được 6 đỉnh để tạo tam giác (trừ đi 2 đỉnh của cạnh đó và 2 đỉnh nằm kề sát cạnh đó), mà có 10 cạnh như thế nên có 10.6 = 60
Suy ra số tgiác được tạo thành từ các đường chéo của đa giác là: 120 - 10 - 60 = 50 tam giác.
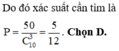
Đúng 0
Bình luận (0)


