tìm số nguyên x , y thỏa mãn sao cho ;
xy + 2x + y + 11 = 0
Tìm các số nguyên x,y thỏa mãn:6xy+4x-9y-7=0
Tìm giá trị nhỏ nhất của A=x^3+y^3+xy với x,y dương thỏa mãn x+y=1
Tìm các số nguyên x,y thỏa mãn 2x^2+1/x^2+y^2/4=4 sao cho xy đạt giá trị lớn nhất
HELP !
a) \(6xy+4x-9y-7=0\)
\(\Leftrightarrow2x.\left(3y+2\right)-9y-6-1=0\)
\(\Leftrightarrow2x.\left(3y+x\right)-3.\left(3y+2\right)=1\)
\(\Leftrightarrow\left(2x-3\right).\left(3y+2\right)=1\)
Mà \(x,y\in Z\Rightarrow2x-3;3y+2\in Z\)
Tự làm típ
\(A=x^3+y^3+xy\)
\(A=\left(x+y\right)\left(x^2-xy+y^2\right)+xy\)
\(A=x^2-xy+y^2+xy\)( vì \(x+y=1\))
\(A=x^2+y^2\)
Áp dụng bất đẳng thức Bunhiakovxky ta có :
\(\left(1^2+1^2\right)\left(x^2+y^2\right)\ge\left(x\cdot1+y\cdot1\right)^2=\left(x+y\right)^2=1\)
\(\Leftrightarrow2\left(x^2+y^2\right)\ge1\)
\(\Leftrightarrow x^2+y^2\ge\frac{1}{2}\)
Hay \(x^3+y^3+xy\ge\frac{1}{2}\)
Dấu "=" xảy ra \(\Leftrightarrow x=y=\frac{1}{2}\)
Cho 2 số x,y là các số nguyên sao cho | x|+| y| =5.Tìm số cặp ( x,y ) thỏa mãn
Tìm các số nguyên thỏa mãn x y sao cho xy+x-y=4
xy+x-y=4
=>(xy+x)-(y+1)=3
=>(y+1)(x-1)=3
Mà x;y nguyên nên (x-1);(y+1) thuộc Ư(3)={1;-1;3;-3}
Đến đây bạn lập bảng là ra
xy+x-y=4
=>(xy+x)-(y+1)=3
=>(y+1)(x-1)=3
Mà x;y nguyên nên (x-1);(y+1) thuộc Ư(3)={1;-1;3;-3}
Đến đây bạn lập bảng là ra
\(x = {-b \pm \sqrt{b^2-4ac} \over 2a}\)
Tìm số nguyên x, y sao cho số phức z = x + yi thỏa mãn z3 = 18 + 26i
A. 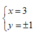
B. 
C. 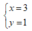
D. 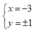
Chọn C.
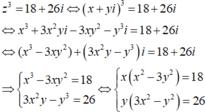
Do x; y nguyên nên
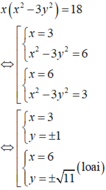
Mà y(3x2 – y2 ) = 26 ⇒ x = 3; y = 1.
Cho 2 số x,y là các số nguyên sao cho | x|+| y| =2.Tìm số cặp ( x,y ) thỏa mãn
ta thấy 2=0+2=2+0=1+1
Trường hợp 1:
Với lxI =0 thì x=0
lyl =2 thì y=-2 hoặc 2
=> với trường hợp 1 thì có 2 cặp (x,y) thỏa mãn là x=0;y=-2 và x=0;y=2.
Trường hợp 2:
Với lxl =2 thì x=-2 hoặc 2
lyl =0 thì y=0
=>với trường hợp 2 thì có 2 cặp (x,y) thỏa mãn là x=-2;y=0 và x=2;y=0.
Trường hợp 3:
Với lxl =1 thì x=-1 hoặc 1
lyl =1 thì y=-1 hoặc 1
=>với trường hợp 3 thì có 4 cặp (x,y) thỏa mãn là x=-1;y=-1
x=-1;y=1
x=1;y=-1
x=1;y=1
Vậy qua 3 trường hợp thì có thì có 4+2+2=8 cặp (x,y) thỏa mãn yêu cầu đề bài.
ta thấy 2=0+2=2+0=1+1
Trường hợp 1:
Với lxI =0 thì x=0
lyl =2 thì y=-2 hoặc 2
=> với trường hợp 1 thì có 2 cặp (x,y) thỏa mãn là x=0;y=-2 và x=0;y=2.
Trường hợp 2:
Với lxl =2 thì x=-2 hoặc 2
lyl =0 thì y=0
=>với trường hợp 2 thì có 2 cặp (x,y) thỏa mãn là x=-2;y=0 và x=2;y=0.
Trường hợp 3:
Với lxl =1 thì x=-1 hoặc 1
lyl =1 thì y=-1 hoặc 1
=>với trường hợp 3 thì có 4 cặp (x,y) thỏa mãn là x=-1;y=-1
x=-1;y=1
x=1;y=-1
x=1;y=1
Vậy qua 3 trường hợp thì có thì có 4+2+2=8 cặp (x,y) thỏa mãn yêu cầu đề bài.
Đúng 5 Không đúng 0 Câu trả lời được Online Math lựa chọncảm ơn nhé đáp án là 8 nha
1) tìm p nguyên tố sao cho : p + 14 và p + 40 cũng nguyên tố
2) Tìm số nguyên tố x,y thỏa mãn
a)x^2 + 45 = y^2
b) Tìm n thuộc N thỏa mãn :3^n +18 là số nguyên tố
c) Tìm x biết : 3^x + 4^x = 5^x
ai lm nhanh mk t cho
p=2 không thỏa
p=3 thỏa
nếu p>3 thì p chia 3 dư 1 hoặc 2
p chia 3 dư 1 => p+14 chia hết cho 3; lớn hơn 3 => vô lí
p chia 3 dư 2 => p+40 chia hết cho 3; lớn hơn 3 => vô lí
vậy p=3
\(\text{ nếu }x=2\text{ thì: }x^2+45=49=7^2\text{ nên }y=7\left(\text{tm}\right)\)
\(+,x>2\text{ thì x lẻ nên }x^2\text{ chia 4 dư 1}\left(\text{bạn tự cm}\right)\)
\(\Rightarrow x^2+45\text{ chia 4 dư 2 nên }y^2\text{ chia 4 dư 2 }\left(\text{vô lí}\right)\)
a)Tìm các số nguyên dương x, y thỏa mãn x+3 chia hết cho y, y+3 chia hết cho x
b)Tìm các số nguyên dương x, y thỏa mãn xy+x+y+2 chia hết cho cả x và y.
tìm các số nguyên dương n sao cho tồn tại các số nguyên dương x,y,z thỏa mãn x^3+y^3+z^3=nx^2y^2z^2
Tìm số nguyên x,y sao cho x-2xy+y=0
Tìm mọi số nguyên thỏa mãn \(x^2-2y^2\) =1