



Giúp mk 20 câu trắc nghiệm này nha
Mọi người giúp mk mấy bài trong ảnh vs thêm 3 câu trắc nghiệm này nhé( gkhi ghi đáp án trắc nghiệm, giải thích rõ giúp mk vs nhé!!!!!)
1. Tìm m để hàm số y=2x/(x-m) xác định với mọi x thuộc (0;1)
A. m ≤ 0 ∨ m ≥ 1 B. m< 0 ∨ m>1
C. m<1 D. m>0
2. Cho 2 tập hợp: A=[2m-1; + ∞) ; B=(- ∞;m+3]. A ∩B khác 0 khi và chỉ khi:
A. m ≤4 B.m ≥3 C.m ≥-4 D. m ≥4
3. Cho 2 tập hợp: A=[-1;3] ; B=[m;m+5]. Để A ∩B=A thì m thuộc tập nào sau đây:
A.[-1;0] B.[-3;-2] C.[-2;-1] D.[1;2]
 GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
GIÚP MK VS!!! MAI MK PHẢI NỘP RỒI!!!!!!!!
1.A. Ta thấy để hàm số xác định thì x-m\(\ne\)0 hay x\(\ne\)m mà vì x\(\in\)(0,1) nên để x\(\ne\)m thì m\(\notin\)(0,1)=>m>=1 hoặc m<=0
2A để A giao B khác 0 thì 2m-1<=m+3 hay m<=4
3C.A giao B =A khi \(\left\{{}\begin{matrix}m< =-1\\m+5>=3\end{matrix}\right.\)\(\Leftrightarrow\left\{{}\begin{matrix}m< =1\\m>=-2\end{matrix}\right.\)
 Các bạn giúp mình phần trắc nghiệm và tự luận nhé . Trắc nghiệm có một số câu ko đúng . Giúp mình nha
Các bạn giúp mình phần trắc nghiệm và tự luận nhé . Trắc nghiệm có một số câu ko đúng . Giúp mình nha
Bài 2:
Áp dụng tính chất của dãy tỉ số bằng nhau,ta được:
\(\dfrac{a}{10}=\dfrac{b}{9}=\dfrac{a-b}{10-9}=90\)
Do đó: a=900; b=810
Giúp mình 60 câu trắc nghiệm này với





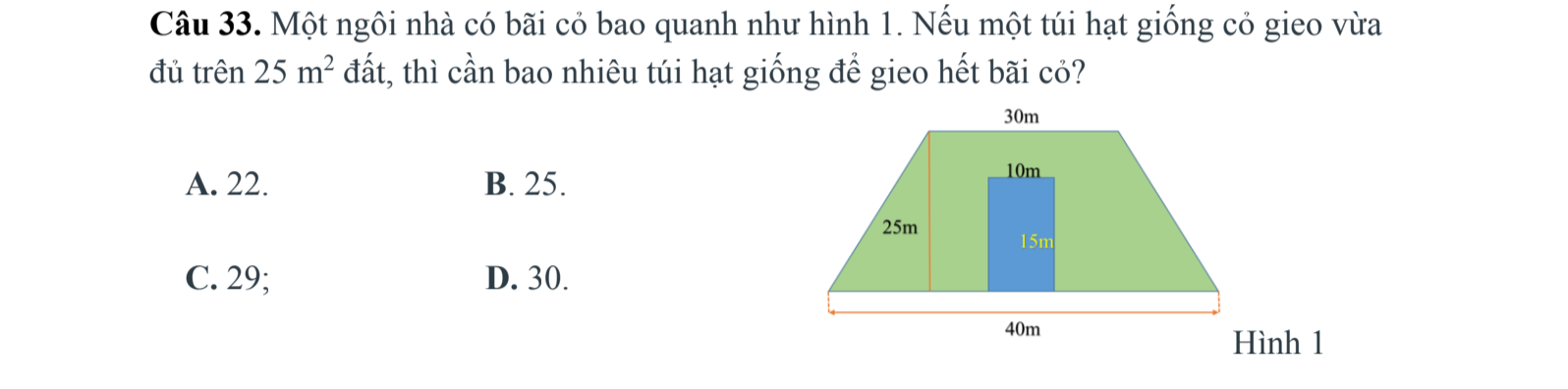
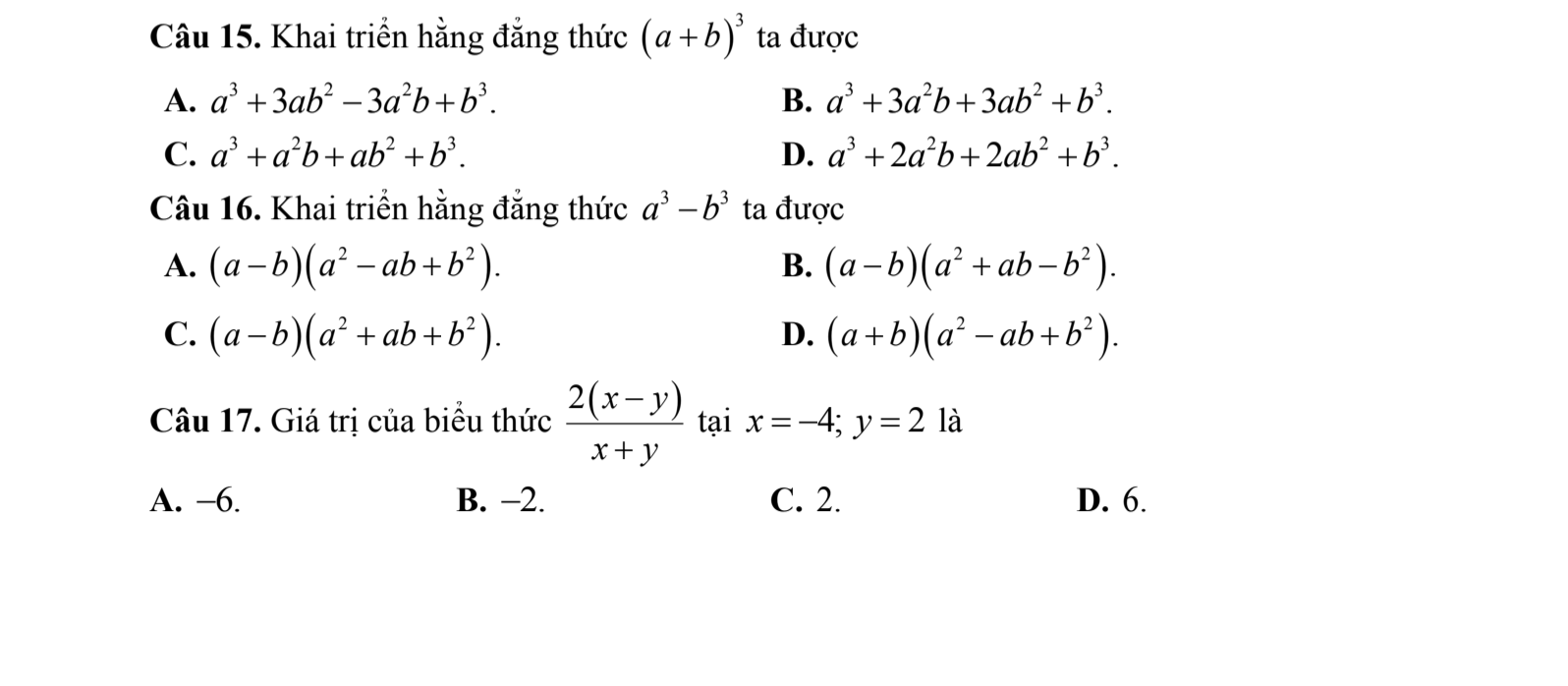


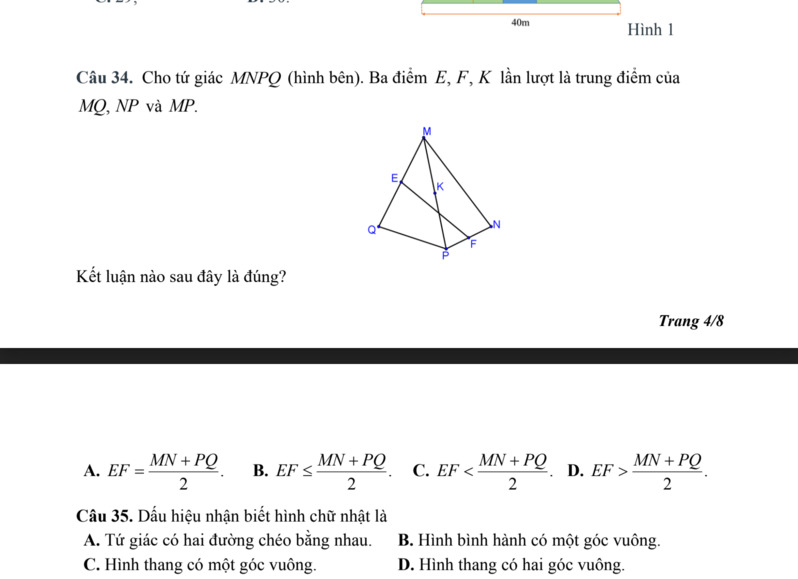

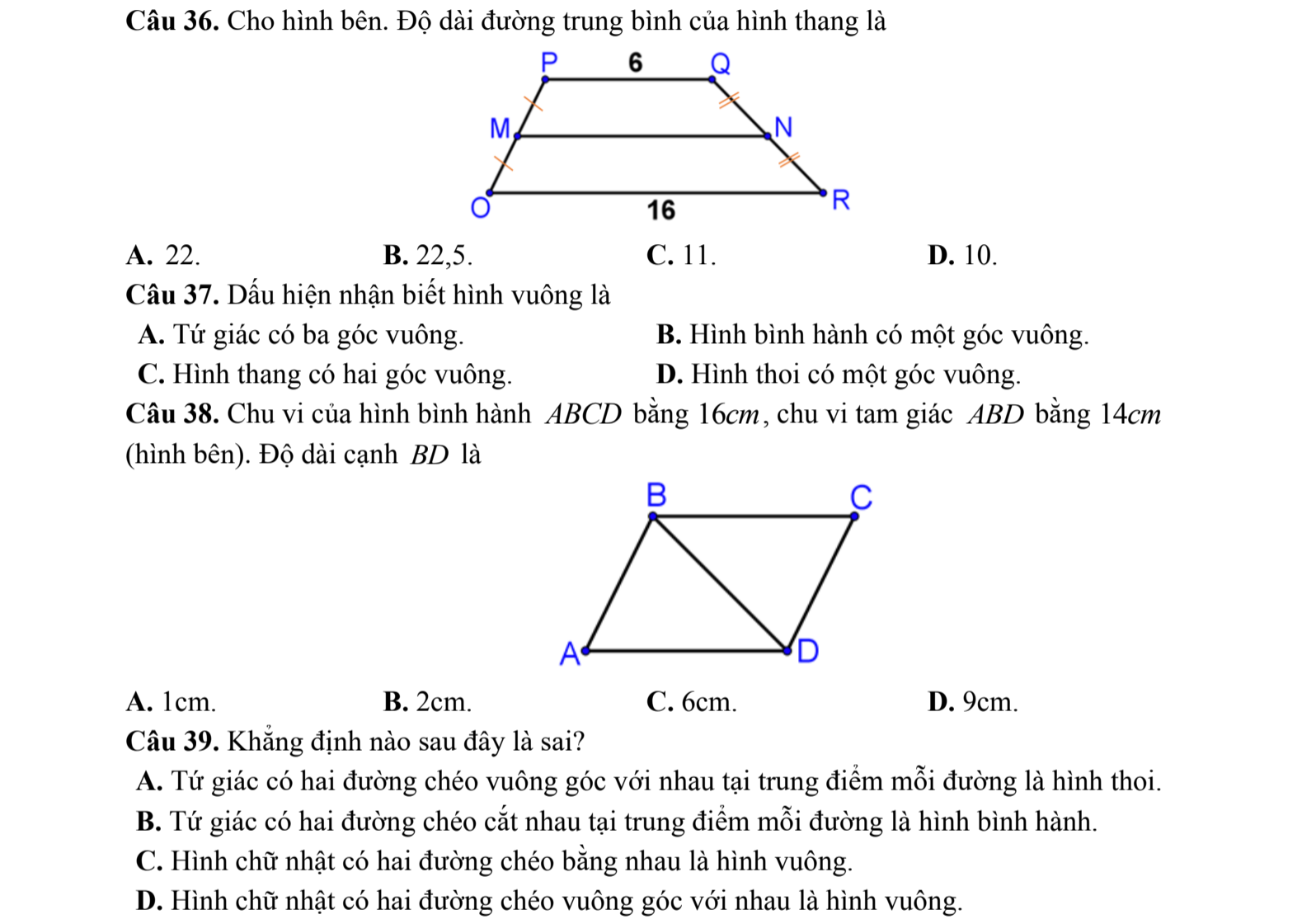


 Giúp em 45 câu trắc nghiệm này vs
Giúp em 45 câu trắc nghiệm này vs
Ai giúp mik câu trắc nghiệm này vs
Giúp mk câu 3 phần trắc nghiệm
Theo định lí Pytago tam giác ABC vuông tại A
\(BC=\sqrt{AB^2+AC^2}=15cm\)
Vì AD là phân giác \(\dfrac{AB}{AC}=\dfrac{BD}{DC}\Rightarrow\dfrac{DC}{AC}=\dfrac{BD}{AB}\)
Theo tc dãy tỉ số bằng nhau
\(\dfrac{DC}{AC}=\dfrac{BD}{AB}=\dfrac{15}{12+9}=\dfrac{15}{21}=\dfrac{5}{7}\Rightarrow BD=\dfrac{45}{7};CD=\dfrac{60}{7}cm\)
Xét tam giác ABC vuông tại A có DE vuông AC
=> DE // AB
Theo hệ quả Ta lét \(\dfrac{DC}{BC}=\dfrac{DE}{AB}\Rightarrow DE=\dfrac{DC.AB}{BC}=\dfrac{36}{7}cm\)
Bài 7: Chứng minh theo quy nạp:
-Khi n=3 thì mệnh đề trở thành:
\(4.5.6=120⋮2^3\)
-Giả sử mệnh đề đúng với n=k tức là:
\(\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)⋮2^k\).
-Ta chứng minh mệnh đề cũng đúng với n=k+1 tức là:
\(\left(k+2\right)\left(k+3\right)\left(k+4\right)...\left(2k\right)\left(2k+1\right)\left(2k+2\right)⋮2^{k+1}\).
-Thật vậy, ta có:
\(\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)⋮2^k\)
\(\Rightarrow2.\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)⋮2^{k+1}\)
\(\Rightarrow2.\left(k+1\right)\left(k+2\right)\left(k+3\right)...\left(2k\right)\left(2k+1\right)⋮2^{k+1}\).
\(\Rightarrow\left(k+2\right)\left(k+3\right)...\left(2k\right)\left(2k+1\right)\left(2k+2\right)⋮2^{k+1}\).
-Vậy mệnh đề cũng đúng với n=k+1. Theo nguyên lý Quy nạp toán học, mệnh đề đúng với mọi n nguyên dương lớn hơn 0.
Giúp e 2 câu trắc nghiệm này vs ạ
Giúp e 2 câu trắc nghiệm này vs ạ
Giúp mình mấy câu trắc nghiệm này với ạ