3. abc > 0 nên trog 3 số phải có ít nhất 1 số dương. 
Vì nếu giả sử cả 3 số đều âm => abc < 0 => trái giả thiết 
Vậy nên phải có ít nhất 1 số dương 

Không mất tính tổng quát, giả sử a > 0 
mà abc > 0 => bc > 0 
Nếu b < 0, c < 0: 
=> b + c < 0 
Từ gt: a + b + c < 0 
=> b + c > - a 
=> (b + c)^2 < -a(b + c) (vì b + c < 0) 
<=> b^2 + 2bc + c^2 < -ab - ac 
<=> ab + bc + ca < -b^2 - bc - c^2 
<=> ab + bc + ca < - (b^2 + bc + c^2) 
ta có: 
b^2 + c^2 >= 0 
mà bc > 0 => b^2 + bc + c^2 > 0 
=> - (b^2 + bc + c^2) < 0 
=> ab + bc + ca < 0 (vô lý) 
trái gt: ab + bc + ca > 0 

Vậy b > 0 và c >0 
=> cả 3 số a, b, c > 0

1.a, Ta có: \(\left(a+b\right)^2\ge4a>0\)

                   \(\left(b+c\right)^2\ge4b>0\)

                    \(\left(a+c\right)^2\ge4c>0\)

\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64abc\)

Mà abc=1

\(\Rightarrow\left[\left(a+b\right)\left(b+c\right)\left(a+c\right)\right]^2\ge64\)

\(\Rightarrow\left(a+b\right)\left(b+c\right)\left(a+c\right)\ge8\left(đpcm\right)\)     

sai rồi. sửa a+b=a+1, b+c=b+1, a+c=c+1 nha, thông cảm, nhìn sai đề

1

\(M=\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}>\frac{a}{a+b+c}+\frac{b}{a+b+c}+\frac{c}{a+b+c}=1\)

\(M=\frac{a}{a+b}+\frac{b}{b+c}+\frac{c}{c+a}< \frac{a+c}{a+b+c}+\frac{b+a}{b+a+c}+\frac{c+b}{a+b+c}=2\)

=> M ko là số tự nhiên

2

\(a+b+c=0\)

\(\Rightarrow\left(a+b+c\right)^2=0\)

\(\Rightarrow a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\)

Do \(a^2+b^2+c^2\ge0\Rightarrow ab+bc+ca\le0\)

3

\(\left(x+y\right)\cdot35=\left(x-y\right)\cdot2010=xy\cdot12\)

\(\Rightarrow35x+35y=2010x-2010y\)

\(\Rightarrow35-2010x=2010y-35y\)

\(\Rightarrow-175x=-245y\)

\(\Rightarrow\frac{x}{y}=\frac{245}{175}=\frac{7}{5}\)

\(\Rightarrow\frac{x}{7}=\frac{y}{5}\)

Đặt \(\frac{x}{7}=\frac{y}{5}=k\)

\(\Rightarrow x=7k;y=5k\)

\(\Rightarrow\left(5k+7k\right)\cdot35=35k^2\cdot12\)

\(\Rightarrow k=k^2\Rightarrow k=1\left(k\ne0\right)\)

Vậy \(x=7;y=5\)

bài 2 chưa thuyết phục lắm, nếu \(a^2+b^2+c^2+2\left(ab+bc+ca\right)=0\) thì \(ab+bc+ca\ge0\) vẫn đúng, lẽ ra phải là \(ab+bc+ca=-\frac{\left(a^2+b^2+c^2\right)}{2}\le0\) *3* 

Ví 1 số :2 dư 0 hoặc 1 mà (a+b) ko chia hết cho 2 => (a+b) :2 dư 1=>1 trong 2 số phải chia hết cho2

Đề sai rồi em, đề đúng phải là:

\(ab\left(x^2+y^2\right)+xy\left(a^2+b^2\right)=ab\)

Vế phải em thiếu a

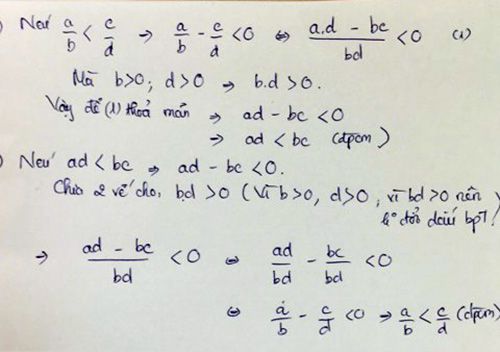
Làm nhắn gọn hơn thì

1
a/b < c/d
=> ad/bd < cb/db
=> ad < cb

2
​ad < cb
=>ad /bd < cb/bd

Chúc pn hc tốt

Làm nhanh trong ngày hôm nay và ngày mai hộ mình nha 

trân thành cảm ơn