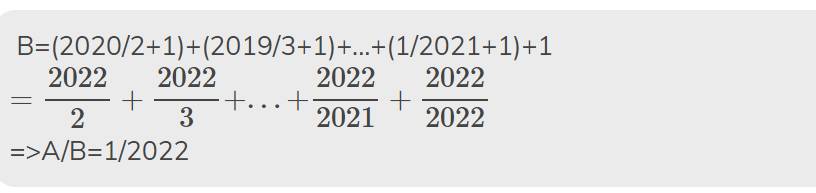A = 2^2020 - 1/ 2^2021 - 1 và B = 2^2021 - 1/ 2^2022 - 1
LL
Những câu hỏi liên quan
1. So sánh
a) \(A=\dfrac{1}{2}+\dfrac{1}{2^2}+\dfrac{1}{2^3}+...+\dfrac{1}{2^{2020}}+\dfrac{1}{2^{2021}}\) và B= \(\dfrac{1}{3}+\dfrac{1}{4}+\dfrac{1}{5}+\dfrac{13}{60}\)
b) \(C=\dfrac{2019}{2021}+\dfrac{2021}{2022}\) và \(D=\dfrac{2020+2022}{2019+2021}.\dfrac{3}{2}\)
a) Ta có:
2A=2.(12+122+123+...+122020+122021)2�=2.12+122+123+...+122 020+122 021
2A=1+12+122+123+...+122019+1220202�=1+12+122+123+...+122 019+122 020
Suy ra: 2A−A=(1+12+122+123+...+122019+122020)2�−�=1+12+122+123+...+122 019+122 020
−(12+122+123+...+122020+122021)−12+122+123+...+122 020+122 021
Do đó A=1−122021<1�=1−122021<1.
Lại có B=13+14+15+1360=20+15+12+1360=6060=1�=13+14+15+1360=20+15+12+1360=6060=1.
Vậy A < B.
Đúng 2
Bình luận (0)
Câu 24: Cho biểu thức: A=1/2+1/3+1/4+.........+1/2021+1/2022 Và B=2021/1+2020/2+2019/3+.........+3/2019+2020+1/2021
B/A
\(=\dfrac{1+\dfrac{2020}{2}+1+\dfrac{2019}{3}+...+1+\dfrac{1}{2021}+1}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}}\)
\(=\dfrac{2022\left(\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}\right)}{\dfrac{1}{2}+\dfrac{1}{3}+...+\dfrac{1}{2021}+\dfrac{1}{2022}}=2022\)
Đúng 1
Bình luận (0)
So sánh:
A = \(\dfrac{2^{2020}-1}{2^{2021}-1}\) và B = \(\dfrac{2^{2021}-1}{2^{2022}-1}\)
\(2.A=\frac{2^{2021}-2}{2^{2021}-1}=1-\frac{1}{2^{2021}-1}\)
\(2B=\frac{2^{2022}-2}{2^{2022}-1}=1-\frac{1}{2^{2022}-1}\)
dó \(\frac{1}{2^{2022}-1}< \frac{1}{2^{2021}-1}\Rightarrow1-\frac{1}{2^{2022}-1}>1-\frac{1}{2^{2021}-1}\Rightarrow A< B\)
HT
so sánh b=1/2022+2/2021+3/2020+...+2021/2+2022/1 VÀ c=1/2+1/3+1/4+...+1/2022+1/2023
B = \(\dfrac{1}{2002}\) + \(\dfrac{2}{2021}\) + \(\dfrac{3}{2020}\)+...+ \(\dfrac{2021}{2}\) + \(\dfrac{2022}{1}\)
B = \(\dfrac{1}{2002}\) + \(\dfrac{2}{2021}\) + \(\dfrac{3}{2020}\)+...+ \(\dfrac{2021}{2}\) + 2022
B = 1 + ( 1 + \(\dfrac{1}{2022}\)) + ( 1 + \(\dfrac{2}{2021}\)) + \(\left(1+\dfrac{3}{2020}\right)\)+ ... + \(\left(1+\dfrac{2021}{2}\right)\)
B = \(\dfrac{2023}{2023}\) + \(\dfrac{2023}{2022}\) + \(\dfrac{2023}{2021}\) + \(\dfrac{2023}{2020}\) + ...+ \(\dfrac{2023}{2}\)
B = 2023 \(\times\) ( \(\dfrac{1}{2023}\) + \(\dfrac{1}{2022}\) + \(\dfrac{1}{2021}\) + \(\dfrac{1}{2020}\)+ ... + \(\dfrac{1}{2}\))
Vậy B > C
Đúng 5
Bình luận (0)
Cho \(A=\dfrac{1}{2}+\dfrac{1}{3}+\dfrac{1}{4}+...+\dfrac{1}{2022}\)
Và \(B = \dfrac{2021}{1}+\dfrac{2020}{2}+\dfrac{2019}{3}+...+\dfrac{1}{2021}\)
Tính B/A
Cho \(\dfrac{x}{2020}+\dfrac{y}{2021}+\dfrac{z}{2022}=1\) và \(\dfrac{2020}{x}+\dfrac{2021}{y}+\dfrac{2022}{z}=0\) \(\left(x,y,z\ne0\right)\)
Chứng minh rằng \(\dfrac{x^2}{2020^2}+\dfrac{y^2}{2021^2}+\dfrac{z^2}{2022^2}=1\)
Bài 1: So sánh phấ số
A= 2020/2021 + 2021/2022 và B= 2020+2021/2021+2022
Bài 2: So Sánh phân số
A= 10^10 -1 / 10^11 -1 va B= 10^10 +1 / 10^11 +1
A = \(\dfrac{2020}{2021}\) + \(\dfrac{2021}{2022}\) ; B = \(\dfrac{2020+2021}{2021+2022}\)
B = \(\dfrac{2020+2021}{2021+2022}\) = \(\dfrac{2020}{2021+2022}\) + \(\dfrac{2021}{2021+2022}\)
\(\dfrac{2020}{2021}\) > \(\dfrac{2020}{2021+2022}\)
\(\dfrac{2021}{2022}\) > \(\dfrac{2021}{2021+2022}\)
Cộng vế với vế ta có:
A = \(\dfrac{2020}{2021}\) + \(\dfrac{2021}{2022}\) > \(\dfrac{2020}{2021+2022}\) + \(\dfrac{2021}{2021+2022}\) = B
Vậy A > B
Đúng 5
Bình luận (0)
A = \(\dfrac{10^{10}-1}{10^{11}-1}\)
A \(\times\) 10 = \(\dfrac{(10^{10}-1)\times10}{10^{11}-1}\) = \(\dfrac{10^{11}-10}{10^{11}-1}\) = 1 - \(\dfrac{9}{10^{11}-1}\) < 1
B = \(\dfrac{10^{10}+1}{10^{11}+1}\)
B \(\times\) 10 = \(\dfrac{(10^{10}+1)\times10}{10^{11}+1}\) = \(\dfrac{10^{11}+10}{10^{11}+1}\) = 1 + \(\dfrac{9}{10^{11}+1}\) > 1
Vì 10 A< 1< 10B
Vậy A < B
Đúng 2
Bình luận (0)
so sánh 2 phân số:
A=\(\dfrac{6^{2020}+1}{6^{2021}+1}\) với B=\(\dfrac{6^{2021}+1}{6^{2022}+1}\)
Lời giải:
$6A=\frac{6^{2021}+6}{6^{2021}+1}=1+\frac{5}{6^{2021}+1}>1+\frac{5}{6^{2022}+1}$
$=\frac{6^{2022}+6}{6^{2022}+1}=6.\frac{6^{2021}+1}{6^{2022}+1}=6B$
$\Rightarrow A>B$
Đúng 0
Bình luận (0)
Cho A = 1/2+1/3+1/4+...+1/2022 và
B = 2021/1+2020/2+2019/3+...+1/2021.
hứa cho đúng
Bạn kiểm tra đề giúp mình! Bạn yêu cầu gì về giả thiết trên?
Đúng 1
Bình luận (0)