GIÚP MÌNH CÂU D VỚI
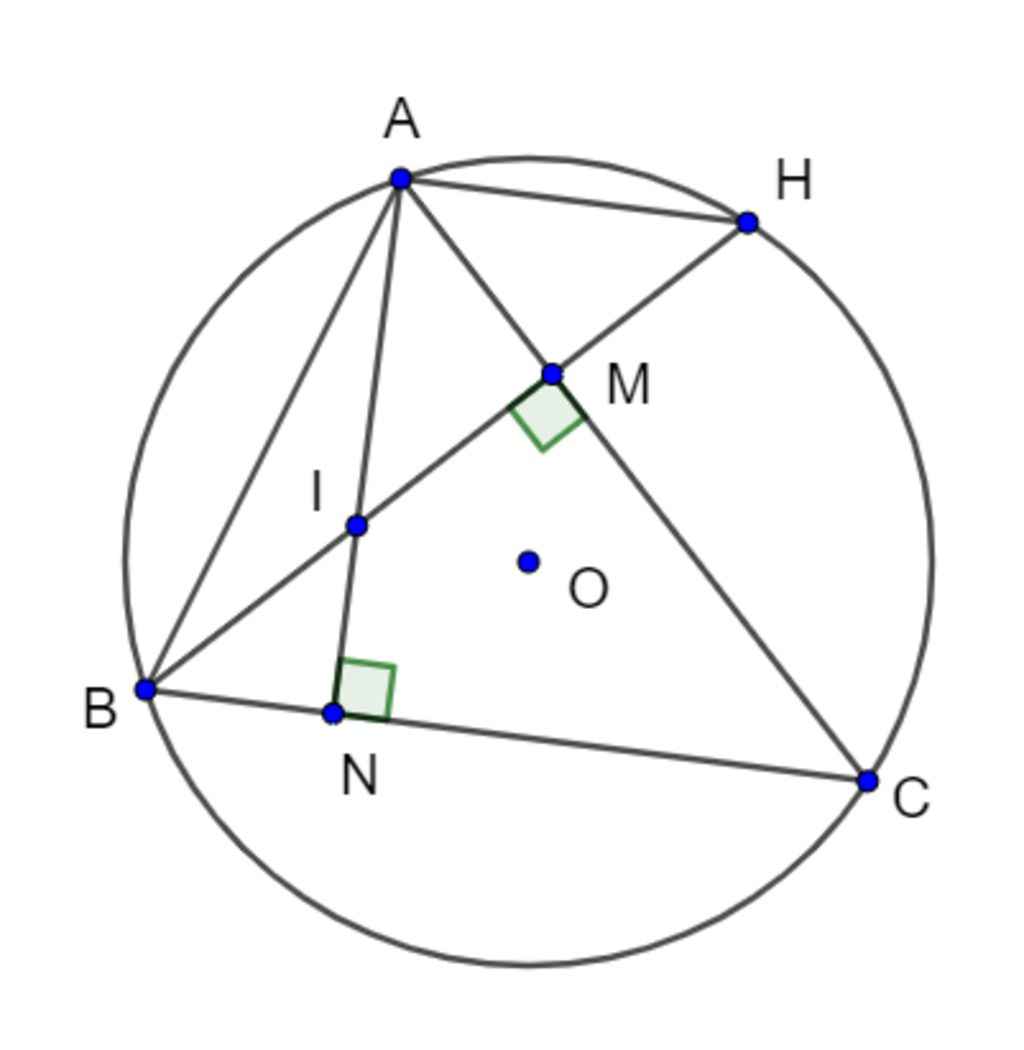
Cho tam giác ABC nhọn nội tiếp (O;R) có BE , CF là các đường cao cắt nhau tại H
a) Chứng Minh Tứ giác BECF nội tiếp. Xác định tâm M của đường tròn này
b) AH cắt BC tại D. Chứng minh DA . Dh = DB . DC
c) Gọi N là điểm đối xứng của H qua M. Chứng minh N thuộc (O) và AN là đường kính của (O)
d) Gọi K là hình chiếu của B trên AN. Chứng minh E, K, M thẳng hàng