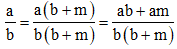b) so sánh: 237 phần 142 và 246 phần 151
HT
Những câu hỏi liên quan
a , Cho phân số a/b (a,b thuộc N , b khác 0 ) Giả sử a/b >1 và m thuộc N, m khác 0. Chứng tỏ rằng a/b>a+m/b+m b, Áp dụng kết quả ở câu a để so sánh 237/142 và 246/151
a) Cho phân số dfrac{a}{b},left(a,binmathbb{N},bne0right)
Giả sử dfrac{a}{b}1 và minmathbb{N},mne0. Chứng tỏ rằng :
dfrac{a}{b}dfrac{a+m}{b+m}
b) Áp dụng kết quả ở câu a) để so sánh : dfrac{237}{142} và dfrac{246}{151}
Đọc tiếp
a) Cho phân số \(\dfrac{a}{b},\left(a,b\in\mathbb{N},b\ne0\right)\)
Giả sử \(\dfrac{a}{b}>1\) và \(m\in\mathbb{N},m\ne0\). Chứng tỏ rằng :
\(\dfrac{a}{b}>\dfrac{a+m}{b+m}\)
b) Áp dụng kết quả ở câu a) để so sánh : \(\dfrac{237}{142}\) và \(\dfrac{246}{151}\)
So sánh:\(\dfrac{237}{142}\) và \(\dfrac{246}{151}\)
* Bài làm:
Vì \(\dfrac{237}{142}\) > 1 => \(\dfrac{237}{142}\) > \(\dfrac{237+9}{142+9}\) hay \(\dfrac{237}{142}\) > \(\dfrac{246}{151}\)
Đúng 0
Bình luận (0)
a) Cho phân số frac{a}{b} ( a, b inN , b ne0 ) Giả sử frac{a}{b} 1 và m in N , m ne 0 . Chứng tỏ rằng :frac{a}{b} frac{a+m}{b+m}b) Áp dụng kết quả ở câu a) để so sánh frac{237}{142} và frac{246}{151}
Đọc tiếp
a) Cho phân số \(\frac{a}{b}\) ( a, b \(\in\)N , b \(\ne\)0 )
Giả sử \(\frac{a}{b}\)> 1 và m \(\in\) N , m \(\ne\) 0 . Chứng tỏ rằng :
\(\frac{a}{b}\) > \(\frac{a+m}{b+m}\)
b) Áp dụng kết quả ở câu a) để so sánh \(\frac{237}{142}\) và \(\frac{246}{151}\)
a ) Nếu \(\frac{a}{b}>\frac{a+m}{b+m}\)
\(\Leftrightarrow a\left(b+m\right)>b\left(a+m\right)\)
\(\Leftrightarrow ab+am>ab+bm\)
\(\Leftrightarrow am>bm\)
\(\Rightarrow a>b\)
\(\Rightarrow\frac{a}{b}>1\)
Vậy \(\frac{a}{b}>1\) thì \(\frac{a}{b}>\frac{a+m}{b+m}\)
b ) Vì 237 > 142 => \(\frac{237}{142}>\frac{237+9}{142+9}=\frac{246}{151}\)
Đúng 0
Bình luận (0)
Xét hiệu :
\(\frac{a}{b}-\frac{a+m}{b+m}\)
\(=\frac{a\left(b+m\right)}{b\left(b+m\right)}-\frac{\left(a+m\right)b}{\left(b+m\right)b}\)
\(=\frac{a.b+a.m}{b\left(b+m\right)}-\frac{a.b+b.m}{b\left(b+m\right)}\)
\(=\frac{a.b+a.m-a.b+b.m}{b\left(b+m\right)}\)
\(=\frac{m\left(a-b\right)}{b\left(b+m\right)}\)
Vì \(\frac{a}{b}>1,b\in\)N* \(\Rightarrow a>b\Rightarrow a-b>0,m\in\)N*
\(\Rightarrow m\left(a-b\right)>0\); Vì : \(b,m\in\)N* \(\Rightarrow b\left(b+m\right)>0\)
\(\Rightarrow\frac{m\left(a-b\right)}{b\left(b+m\right)}>0\) hay : \(\frac{a}{b}-\frac{a+m}{b+m}>0\Rightarrow\frac{a}{b}>\frac{a+m}{b+m}\)
Vậy \(\frac{a}{b}>1,m\in\)N* thì \(\frac{a}{b}>\frac{a+m}{b+m}\)
b, Tự làm
Đúng 0
Bình luận (0)
a/ Cho phân số \(\frac{a}{b}\) (a,b \(\in\) N, b\(\ne\) 0)
Giả sử \(\frac{a}{b}\) >1 mà m \(\in\) N, m\(\ne\) 0. Chứng tỏ rằng :
\(\frac{a}{b}>\frac{a+m}{b+m}\)
b./Áp dụng kết quả ở câu a để so sánh: \(\frac{237}{142}và\frac{246}{151}\)
1a) cho phân số frac{a}{b} ( a,bin N,bne0)Giả sử frac{a}{b} 1 và m inN, m ne0. Chứng tỏ rằng:frac{a}{b} frac{a+m}{b+m}b) Áp dụng kết quả ở câu a) để so sánh frac{434}{561}và frac{441}{568}2a) Cho phân số frac{a}{b}( a,b inN, bne0)b) Áp dụng kết quả ở câu a) để so sánh frac{237}{142}và frac{246}{151}( giúp giải câu này với)
Đọc tiếp
1a) cho phân số \(\frac{a}{b}\) ( \(a,b\in N,b\ne0\))
Giả sử \(\frac{a}{b}\)< 1 và m \(\in\)N, m \(\ne\)0. Chứng tỏ rằng:
\(\frac{a}{b}\) < \(\frac{a+m}{b+m}\)
b) Áp dụng kết quả ở câu a) để so sánh \(\frac{434}{561}\)và \(\frac{441}{568}\)
2a) Cho phân số \(\frac{a}{b}\)( a,b \(\in\)N, b\(\ne\)0)
b) Áp dụng kết quả ở câu a) để so sánh \(\frac{237}{142}\)và \(\frac{246}{151}\)
( giúp giải câu này với)
Bài 1 Tìm hai phân số khác nhau,các phấn số này lớn hơn 1/5 nhưng nhỏ hơn 1/4.Bài 2 : a) Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b 1 và m thuộc tập hợp N,m khác 0 . Chứng tỏ rằng a/ba+m/b+mb) Áp dụng kết quả ở câu a) để só sánh 434/561 và 441/568Bài 3 : Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b 1 và m thuộc tập hợp N,m khác 0.Chứng tỏ rằng a/ba+m/b+mb) Áp dụng kết quả ở câu a) để só sánh: 237/142 và 246/151Bài 4: So sánh : A1718+1/1719+1 và B 1717+1/1718+1B...
Đọc tiếp
Bài 1 Tìm hai phân số khác nhau,các phấn số này lớn hơn 1/5 nhưng nhỏ hơn 1/4.
Bài 2 : a) Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b < 1 và m thuộc tập hợp N,m khác 0 . Chứng tỏ rằng
a/b<a+m/b+m
b) Áp dụng kết quả ở câu a) để só sánh 434/561 và 441/568
Bài 3 : Cho phân số a/b (a,b thuộc tập hợp N , b khác 0. Giả sử a/b > 1 và m thuộc tập hợp N,m khác 0.Chứng tỏ rằng
a/b>a+m/b+m
b) Áp dụng kết quả ở câu a) để só sánh: 237/142 và 246/151
Bài 4: So sánh : A=1718+1/1719+1 và B = 1717+1/1718+1
Bài 5 : So sánh : C=9899+1/9889+1 và D = 9898+1/9888+1
a/ Cho phân số \(\frac{a}{b}\) (a,b \(\in\) N, b\(\ne\) 0)
Giả sử \(\frac{a}{b}\) >1 mà m \(\in\) N, m\(\ne\) 0. Chứng tỏ rằng :
\(\frac{a}{b}>\frac{a+m}{b+m}\)
b./Áp dụng kết quả ở câu a để so sánh: \(\frac{237}{142}và\frac{246}{151}\)
a/ Cho phân số \(\frac{a}{b}\) (a,b \(\in\) N, b\(\ne\) 0)
Giả sử \(\frac{a}{b}\) >1 mà m \(\in\) N, m\(\ne\) 0. Chứng tỏ rằng :
\(\frac{a}{b}>\frac{a+m}{b+m}\)
b./Áp dụng kết quả ở câu a để so sánh: \(\frac{237}{142}và\frac{246}{151}\)
a) Vì a/b > 1 nên a > b
Ta có: \(\frac{a}{b}-\frac{a+m}{b+m}=\frac{a\left(b+m\right)-b\left(a+m\right)}{b\left(b+m\right)}=\frac{m\left(a-b\right)}{b\left(b+m\right)}>0\)
=> \(\frac{a}{b}>\frac{a+m}{b+m}\)
b) lấy a=237, b= 142; m = 9
\(\frac{237}{142}>\frac{237+9}{142+9}\)
Đúng 0
Bình luận (0)
mệt rồi mình nghỉ đây tối mình giải cho
Đúng 0
Bình luận (0)
Lưu ý:Có 5 cách so sánh phân số - Quy đòng mẫu-Quy đồng tử-So sánh với 1-So sánh phần bù phần hơn-So sánh phân số trung gianBài 1: So Sánh phân số:1) 33/12 và 49/12 2) 14/23 và 21/37 3) 17/6 và 56/21 4) 26/39 và 51/685)43/45 và 61/63 6) 139/135 và 237/233 7) a+2/a+1 và a+3/ a+2 (a là số tự nhiên )8) 16/33 và 55/108 9) 16/45 và 23/91 10) 32/47 và 99/151
Đọc tiếp
Lưu ý:Có 5 cách so sánh phân số
- Quy đòng mẫu
-Quy đồng tử
-So sánh với 1
-So sánh phần bù phần hơn
-So sánh phân số trung gian
Bài 1: So Sánh phân số:
1) 33/12 và 49/12 2) 14/23 và 21/37 3) 17/6 và 56/21 4) 26/39 và 51/68
5)43/45 và 61/63 6) 139/135 và 237/233 7) a+2/a+1 và a+3/ a+2 (a là số tự nhiên )
8) 16/33 và 55/108 9) 16/45 và 23/91 10) 32/47 và 99/151
5) 43/45 và 61/63 gần bằng 1 ( 45/45 hoặc 63/63)
45/45-43/45=2/45
63/63-61/63=2/63
Vì 43/45 kém 45/45 là 2/45
Còn 61/63 kém 63/63 là 2/63
2/45>2/65 => 43/45<63/65
6) tương tự con 5)
7) bó tay
Đúng 0
Bình luận (0)
8) bó tay
9) lấy phân số trung gian là 16/91
16/45 <16/91<23/91
=> 16/45 <23 /91
10) bó tay
Đúng 0
Bình luận (0)
sai. có 10 cách để so sánh phân số
-
Đúng 0
Bình luận (0)
Xem thêm câu trả lời