giải câu d và e cho mik với
T1
Những câu hỏi liên quan
cho tam giác ABC có góc A=60 độ. vẽ ra phía ngoài tam giác đó các tam giác đều ABM và ACN. gọi D là giao điểm của AB với CM, E là giao điểm của AC với BN.
a) cmr: tam giác ADE đều ( mik giải đc câu này r nha)
b) cho biết BD=4,EC=9. tính DE
giải giúp mik câu b nha
giải giúp mik bài này với, giải mỗi câu c thôi cũng đượccho tam giác ABC có ABAC(A nhỏ hơn 90 độ). gọi H là trung điểm BCa/ chứng minh tam giác ABH tam giác ACH và AH là tia phân giác góc BACb/ vẽ HD vuông góc với AC tại D. trên cạnh AB lấy E sao cho AEAD. tính số đo góc AEHc/gọi M là giao điểm 2 tia AB và DH, đường thẳng qua M và song song với ED cắt tia AC tại N. chứng minh N,H,E thẳng hàngnhắc lại là giải mỗi câu c cũng được nha, giải nhanh giúp mình mình tick cho
Đọc tiếp
giải giúp mik bài này với, giải mỗi câu c thôi cũng được
cho tam giác ABC có AB=AC(A nhỏ hơn 90 độ). gọi H là trung điểm BC
a/ chứng minh tam giác ABH= tam giác ACH và AH là tia phân giác góc BAC
b/ vẽ HD vuông góc với AC tại D. trên cạnh AB lấy E sao cho AE=AD. tính số đo góc
AEH
c/gọi M là giao điểm 2 tia AB và DH, đường thẳng qua M và song song với ED cắt tia AC tại N. chứng minh N,H,E thẳng hàng
nhắc lại là giải mỗi câu c cũng được nha, giải nhanh giúp mình mình tick cho
hình chương mấy đấy
trong đề cương ôn thì học kì
a)Xét \(\Delta ABH\)và \(\Delta ACH\)có:
\(AB=AC\left(gt\right)\)
\(AH:\)cạnh chung
\(HB=HC\)(H: trung điểm BC)
\(\Rightarrow\Delta ABH=\Delta ACH\left(c.c.c\right)\)
\(\Rightarrow\widehat{BAH}=\widehat{CAH}\)(hai cạnh tương ứng)
\(\Rightarrow AH\)là pg\(\widehat{BAC}\)
b)Xét \(\Delta AEH\)và \(\Delta ADH\)có:
\(AE=AD\left(gt\right)\)
\(\widehat{EAH}=\widehat{DAH}\left(cmt\right)\)
\(AH:\)cạnh chung
\(\Rightarrow\Delta AEH=\Delta ADH\left(c.g.c\right)\)
\(\Rightarrow\widehat{AEH}=\widehat{ADH}\)(hai cạnh tương ứng)
\(\Rightarrow\widehat{AEH}=90^o\)
c) Câu này mình thấy sao ấy, nếu M là gđ của AB và DH thì sao được.
Ta có:
\(AE\perp EH\)
\(DH\perp EH\)
\(\Rightarrow AE//DH\)
\(\Rightarrow AB//DH\)
\(\Rightarrow AB;DH\)không có điểm chung
các bạn giải hộ mik câu D,E,F nha![]()
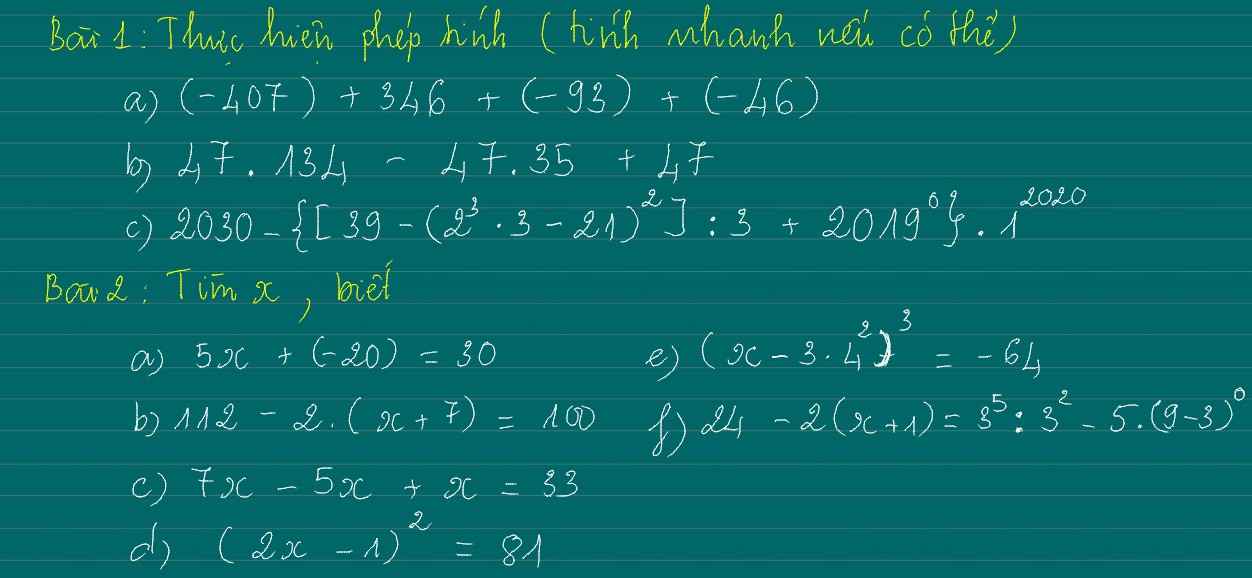
Bài 2:
d: \(\Leftrightarrow\left[{}\begin{matrix}2x-1=9\\2x-1=-9\end{matrix}\right.\Leftrightarrow\left[{}\begin{matrix}x=5\\x=-4\end{matrix}\right.\)
Đúng 0
Bình luận (0)
\(f.24-2\left(x+1\right)=3^5:3^2-5.\left(9-3\right)^0\\24-2\left(x+1\right)=3^3-5.6^0\\ 24-2\left(x+1\right)=27-5.1\\ 24-2\left(x+1\right)=27-5\\ 24-2\left(x+1\right)=22\\ 2\left(x+1\right)=24-22\\ 2\left(x+1\right)=2\\ x+1=2:2\\ x+1=1\\ x=1-1\\ x=0\)
Đúng 1
Bình luận (0)
d, (2x-1)2= 81 e, (x-3.4^2)3= 64
=> (2x-1)2= 92 (x-3.16)3= 4^3
=> 2x-1=9 x-48 = 4
=> 2x=10 x = 4+48= 52
=> x= 10:2 Vậy...
=> x=5
Vậy ...
Đúng 0
Bình luận (2)
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB=9cm, HC=16cm
a) Tính AB,AC,AH (MIK GIẢI CÂU NÀY RR CÁC BẠN KO CẦN GIẢI ĐÂU NHA)
b) Gọi D và E lần lượt hình chiếu của H trên AB và AC. Tứ giác ADHE là hình gì? Chứng minh
c) Tính chu vi và diện tích của tứ giác ADHE
CÁC BẠN GIẢI GIÚP MIK NHA MIK SẼ TICK CHO CÁC BẠN CẢM ƠN CÁC BẠN NHÌU
Giải :
Ta có hình vẽ :
a ) Ta có :
+ ) \(AH^2=BH.CH=9.16=144cm^2\)
\(\Rightarrow AH=12cm\)
+ ) \(AB^2=BH.BC=9.25=225cm^2\)
\(\Rightarrow AB=15cm\)
+ ) \(AC^2=CH.BC=16.25=400cm^2\)
\(\Rightarrow AC=20cm\)
b ) Chứng minh được tứ giác ADHE là hình chữ nhật
c ) Ta có :
+ ) \(HD.AB=HA.HB\)
\(\Rightarrow HD=\frac{HA.HB}{AB}=\frac{12.9}{15}=7,2cm\)
+ ) \(HE.AC=HA.HC\)
\(\Rightarrow HE=\frac{HA.HC}{AC}=\frac{12.16}{20}=9,6cm\)
\(\Rightarrow P\left(ADHE\right)=\left(7,2+9,6\right).2=33,6\left(cm\right)\)
\(\Rightarrow S\left(ADHE\right)=7,2\times9,6=69,12\left(cm^2\right)\)
Đúng 0
Bình luận (0)
Giải giúp mik câu d), chỉ câu d thôi nhanh đi mik cần gấp =(
Cho tam giác ABC vuông tại A cho AB =6cm, AC = 8cm
a) Tính BC
b) Vẽ đường phân giác của góc B cắt AC tại D. Vẽ DE vuông góc BC (E thuộc BC). Chứng minh tam giác ABD = tam giác EBD
c) So sánh AD và DC
d) Trên tia đối của tia AB lấy điểm K sao cho AK = EC. Chứng minh: góc BKC = góc BCK
d: BK=BA+AK
BC=BE+EC
mà BA=BE và AK=EC
nên BK=BC
=>góc BKC=góc BCK
Đúng 0
Bình luận (0)
Cho tam giác ABC vuông tại A, đường cao AH. Biết HB=9cm,HC=16cm
a)Tính AB,AC,AH
b)Gọi D và E lần lượt là hình chiếu của H trên AB và AC. Tứ giác ADHE là hình gì? Chứng minh
c)Tính chu vi và diện tích của tiws giác ADHE
CÁC BẠN GIẢI GIÚP MIK CÂU B VÀ C THÔI NHA CÂU A MIK GIẢI RR CẢM ƠN CÁC BẠN NHÌU =) =)
áp dụng hệ thức lượng vào tam giác vuông ABC có AH^2=BH.CH=9.16=144 nên AH=12 , áp dụng định lý pytago vào 2 tam giác ABH ,AHC ta được AB=15,AC=20 ADHE là hình chữ nhật vi có 3 góc=90độ áp dụng hệ thức lượng ta tính được AD và DH
Đúng 0
Bình luận (0)
Giải giúp mk câu 1 a, b, c, d, e, f nha mik cần gấp
Em đưa cả ngữ liệu và đề bài đầy đủ lên đây để thầy cô và các bạn trong cộng đồng có thể hỗ trợ nhé!
Đúng 0
Bình luận (0)
Các bạn giải giúp mik câu này nha: x+y=4 x*y=2 tính D=x^4+y^4 và E=x^5 +y^5
Xem nào...hmm...
\(D=x^4+y^4=\left(x^2+y^2\right)^2-2x^2y^2\)
\(=\left[\left(x+y\right)^2-2xy\right]^2+2.\left(xy\right)^2\)
Thay x + y = 4 , xy = 2 vào ta được ...
\(E=\left(x^4+y^4\right)\left(x+y\right)-xy\left(x^3+y^3\right)\)
\(=D\left(x+y\right)-2\left(x+y\right)\left(x^2-xy+y^2\right)\)
\(=4D-8\left[\left(x+y\right)^2-3xy\right]\)
Thay lần lượt D ở câu trên, x + y = 4, xy = 3 vào...
Đúng 0
Bình luận (0)
Cho tam giác ABC cân tại A. Trên tia đối của AB và AC, kẻ D và E sao cho BD = CE a) chứng minh tam giác ADE cân, DE//BC b) Từ D kẻ DM vuông góc với BC, từ E kẻ EN vuông góc với BC. Cm DM=EN c) chứng minh tam giác AMN là tam giác cân ( giải hộ mik nhanh nha)
a, Ta có : AD = AB + BD ; AE = AC + CE
mà AB = AC (gt); BD = CE (gt)
=> AD = AE
Vậy tam giác ADE cân tại A
Ta có : \(\dfrac{AB}{AD}=\dfrac{AC}{AE}\)do AB = AC; AD = AE(cmt)
=> DE // BC ( Ta lét đảo )
b, Vì ^ABC = ^MDB ( đối đỉnh )
^ACB = ^NCE ( đối đỉnh )
mà ^ABC = ^ACB ( tam giác ABC cân tại A )
=> ^MDB = ^NCE
Xét tam giác DMB và tam giác ENC có :
BD = EC (cmt)
^MDB = ^NCE ( cmt )
Vậy tam giác DMB = tam giác ENC ( ch - gn )
=> DM = EN ( 2 cạnh tương ứng )
=> BM = NC ( 2 cạnh tương ứng )
c, Ta có : ^ABM = ^MBC - ^ABC
^ACN = ^NCM = ^ACB
=> ^ABM = ^ACN
Xét tam giác ABM và tam giác ACN có :
AB = AC (gt)
^ABM = ^ACN (cmt)
BM = CN (cmt)
Vậy tam giác ABM = tam giác ACN ( c.g.c )
=> ^AMB = ^ANC ( 2 góc tương ứng )
Xét tam giác AMN có : ^AMB = ^ANC (cmt)
Vậy tam giác AMN cân tại A
Đúng 1
Bình luận (0)
Bạn vẽ hình giúp mình nha
a. Tam giác ABC cân tại A nên AB=AC
Ta có: AE=AC+CE, AD=AB+BD
Mà AC=AB, CE=BD
\(\Rightarrow AE=AD\) \(\Rightarrow\Delta ADE\) cân tại A
Xét \(\Delta ADE\) có: \(\dfrac{AB}{BD}=\dfrac{AC}{CE}\)
Áp dụng định lí Ta-let đảo \(\Rightarrow BC//DE\) (đpcm)
Xét \(\Delta BDM\) vuông tại M và \(\Delta CEN\) vuông tại N có:
\(\left\{{}\begin{matrix}BD=CE\\\widehat{MBD}=\widehat{NEC}\left(cùng.bằng.\widehat{ABC}\right)\end{matrix}\right.\)
\(\Rightarrow\)\(\Delta BDM\)=\(\Delta CEN\) \(\Rightarrow\)DM=EN (đpcm)
Kẻ \(AH\perp BC\) \(\left(H\in BC\right)\)
Ta có \(\Delta ABC\) cân tại A nên AH vừa là đường cao vừa là đường trung tuyến
\(\Rightarrow BH=CH\)
Mà MB=CN (\(\Delta BDM\)=\(\Delta CEN\)) \(\Rightarrow AM=AN\)
\(\Rightarrow\Delta AMN\) cân tại A
Đúng 1
Bình luận (0)




