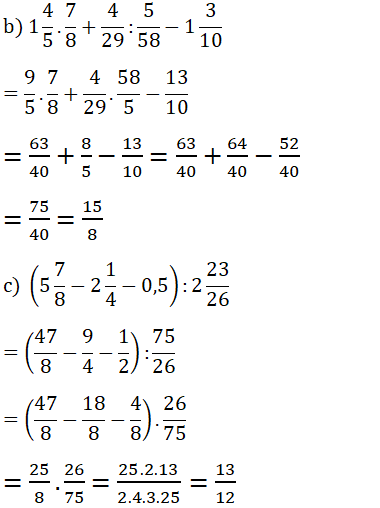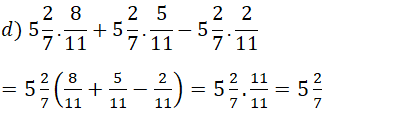Tính: \(B=\frac{1}{2}-\frac{1}{2^4}+\frac{1}{2^7}-\frac{1}{2^{10}}+...-\frac{1}{2^{58}}\)
LA
Những câu hỏi liên quan
Tính D = \(\frac{1}{2}-\frac{1}{2^4}+\frac{1}{2^7}-\frac{1}{2^{10}}+...-\frac{1}{2^{58}}\)
\(\frac{1}{2^3}\)D= \(\frac{1}{2^4}-\frac{1}{2^7}+\frac{1}{2^{10}}-\frac{1}{2^{13}}+...+\frac{1}{2^{58}}-\frac{1}{2^{61}}\)
D+ \(\frac{1}{2^3}\)D=\(\frac{1}{2}-\frac{1}{2^4}+\frac{1}{2^4}+\frac{1}{2^7}-\frac{1}{2^7}-\frac{1}{2^{10}}+\frac{1}{2^{10}}+...-\frac{1}{2^{58}}+\frac{1}{2^{58}}-\frac{1}{2^{61}}\)
\(\frac{9}{8}\)D= \(\frac{1}{2}-\frac{1}{2^{61}}\)=> D= \(\frac{\frac{1}{2}-\frac{1}{2^{61}}}{\frac{9}{8}}\)
Đúng 0
Bình luận (0)
Tính D, biết
D=\(\frac{1}{2}-\frac{1}{2^4}+\frac{1}{2^7}-\frac{1}{2^{10}}+........-\frac{1}{2^{58}}\)
\(D=\frac{1}{2}-\frac{1}{2^4}+\frac{1}{2^7}-\frac{1}{2^{10}}+...+\frac{1}{2^{55}}-\frac{1}{2^{58}}\)
\(\Rightarrow2^3D=2^2-\frac{1}{2}+\frac{1}{2^4}-\frac{1}{2^7}+....+\frac{1}{2^{52}}-\frac{1}{2^{55}}\)
\(\Rightarrow8D+D=2^2-\frac{1}{2^{58}}\)
\(\Rightarrow D=\frac{2^2-\frac{1}{2^{58}}}{9}\)
Đúng 0
Bình luận (0)
Tính
\(D=\frac{1}{2}-\frac{1}{2^4}+\frac{1}{2^7}-\frac{1}{2^{10}}+...+\frac{1}{2^{57}}-\frac{1}{2^{58}}\)
tính:
D= \(\frac{1}{2}-\frac{1}{2^4}+\frac{1}{2^7}-\frac{1}{2^{10}}+...-\frac{1}{2^{58}}\)
Tính nhanh :
1)A=\(\frac{1}{2}-\frac{1}{2^2}+\frac{1}{2^3}-...+\frac{1}{2^{99}}-\frac{1}{2^{100}}\)
2)B=\(\frac{1}{2}+\frac{1}{2^3}+\frac{1}{2^5}+...+\frac{1}{2^{99}}\)
3)C=\(\frac{1}{2}-\frac{1}{2^4}+\frac{1}{2^7}-\frac{1}{2^{10}}+...-\frac{1}{2^{58}}\)
\(2A=1-\frac{1}{2}+\frac{1}{2^2}-\frac{1}{2^3}+.....-\frac{1}{2^{99}}\Rightarrow2A+A=3A=\left(1-\frac{1}{2}+\frac{1}{2^2}-....-\frac{1}{2^{99}}\right)+\left(\frac{1}{2}-\frac{1}{2^2}+......-\frac{1}{2^{100}}\right)=1-\frac{1}{2^{100}}=\frac{2^{100}-1}{2^{100}}\Rightarrow A=\frac{2^{100}-1}{3.2^{100}}\)
\(2,4B=2+\frac{1}{2}+\frac{1}{2^3}+.....+\frac{1}{2^{97}}\Rightarrow4B-B=3B=\left(2+\frac{1}{2}+....+\frac{1}{2^{97}}\right)-\left(\frac{1}{2}+\frac{1}{2^3}+...+\frac{1}{2^{99}}\right)=2-\frac{1}{2^{99}}=\frac{2^{100}-1}{2^{99}}\Rightarrow B=\frac{2^{100}-1}{3.2^{99}}\)
\(3,C=\frac{1}{2}-\frac{1}{2^4}+\frac{1}{2^7}-....-\frac{1}{2^{58}}\Rightarrow8C=4-\frac{1}{2}+\frac{1}{2^4}-.....-\frac{1}{2^{55}}\Rightarrow8C+C=9C=\left(4-\frac{1}{2}+\frac{1}{2^4}-....-\frac{1}{2^{55}}\right)+\left(\frac{1}{2}-\frac{1}{2^4}+\frac{1}{2^7}-....-\frac{1}{2^{58}}\right)=4-\frac{1}{2^{58}}=\frac{2^{60}-1}{2^{58}}\Rightarrow C=\frac{2^{60}-1}{9.2^{58}}\)
Đúng 0
Bình luận (0)
a, 20,7+1,47:7-0,23.5
b,\(1\frac{4}{5}.\frac{7}{8}+\frac{4}{29}:\frac{5}{58}-1\frac{3}{10}\)
c, \(\left(5\frac{7}{8}-2\frac{1}{1}-0,5\right):2\frac{23}{26}\)
d, \(5\frac{2}{7}.\frac{8}{11}+5\frac{2}{7}.\frac{5}{11}-5\frac{2}{7}.\frac{2}{11}\)
a) 20,7 + 1,47 : 7 - 0,23 . 5
= 20,7 + 0,21 – 1,15
= 20,91 – 1,15
= 19,76
Ở trên vietjack có đó bn =)
Đúng 0
Bình luận (0)
a, 20,7 + 1,47 : 7 - 0,23 . 5
=\(\frac{207}{10}+\frac{147}{100}:7-\frac{23}{100}.5\)
= \(\frac{207}{10}+\frac{21}{100}-\frac{23}{20}\)
= \(\frac{2091}{100}+\frac{-23}{20}\)
= \(\frac{494}{25}\)
Đúng 0
Bình luận (0)
\(a,20,7+1,47:7-0,23\cdot5\)
\(=20,7+0,21-1,15=19,76\)
\(b,1\frac{4}{5}\cdot\frac{7}{8}+\frac{4}{29}:\frac{5}{58}-1\frac{3}{10}\)
\(=\frac{9}{5}\cdot\frac{7}{8}+\frac{4}{29}:\frac{5}{58}-\frac{13}{10}\)
\(=\frac{9\cdot7}{5\cdot8}+\frac{4}{29}\cdot\frac{58}{5}-\frac{13}{10}\)
\(=\frac{63}{40}+\frac{4}{1}\cdot\frac{2}{5}-\frac{13}{10}\)
\(=\frac{63}{40}+\frac{8}{5}-\frac{13}{10}=\frac{63}{40}+\frac{64}{40}-\frac{52}{40}=\frac{63+64-52}{40}=\frac{75}{40}=\frac{15}{8}\)
Đúng 0
Bình luận (0)
Xem thêm câu trả lời
a,A=\(2\frac{1}{2}:\left(\frac{-1}{2}\right)^2-\frac{1}{-3}.\left(\frac{-1}{2}-\frac{4}{3}:\frac{-8}{9}\right)\)
b,B=\(\left(3\frac{10}{99}+4\frac{11}{99}-\frac{58}{299}\right).\left(\frac{1}{2}-\frac{4}{3}-\frac{1}{6}\right)\)
Trả lời
B=(3 10/99+4 11/99-58/299).(1/2-4/3-1/6)
=(......................................).0
=0.
Đúng 0
Bình luận (0)
a, Tính : frac{left(13frac{1}{4}-2frac{5}{27}-10frac{5}{6}right).230frac{1}{25}+46frac{3}{4}}{left(1frac{3}{10}+frac{10}{3}right):left(12frac{1}{3}-14frac{2}{7}right)}b, Tính : Pfrac{frac{1}{2}+frac{1}{3}+frac{1}{4}+...+frac{1}{2012}}{frac{2011}{1}+frac{2010}{2}+frac{2009}{3}+...+frac{1}{2011}}c, Tính : frac{left(1+2+3+...+99+100right)left(frac{1}{2}-frac{1}{3}-frac{1}{7}-frac{1}{9}right)left(63.1,2-21.3,6right)}{1-2+3-4+...+99-100}
Đọc tiếp
a, Tính : \(\frac{\left(13\frac{1}{4}-2\frac{5}{27}-10\frac{5}{6}\right).230\frac{1}{25}+46\frac{3}{4}}{\left(1\frac{3}{10}+\frac{10}{3}\right):\left(12\frac{1}{3}-14\frac{2}{7}\right)}\)
b, Tính : \(P=\frac{\frac{1}{2}+\frac{1}{3}+\frac{1}{4}+...+\frac{1}{2012}}{\frac{2011}{1}+\frac{2010}{2}+\frac{2009}{3}+...+\frac{1}{2011}}\)
c, Tính : \(\frac{\left(1+2+3+...+99+100\right)\left(\frac{1}{2}-\frac{1}{3}-\frac{1}{7}-\frac{1}{9}\right)\left(63.1,2-21.3,6\right)}{1-2+3-4+...+99-100}\)
Bài 1 : Tính tổng S , biết : \(S=\frac{1}{1\times2}+\frac{1}{2\times3}+\frac{1}{3\times4}+....+\frac{1}{2010\times2011}\)
Bài 2 : Tính tổng sau : \(S=\frac{3}{10\times13}+\frac{3}{13\times16}+\frac{3}{16\times19}+....+\frac{3}{58\times61}\)
Bài 3 : Tính tổng sau : \(S=\frac{1}{4\times7}+\frac{1}{7\times10}+\frac{1}{10\times13}+....+\frac{1}{19\times22}\)
Bài 1 :
\(S=\frac{1}{1}-\frac{1}{2}+\frac{1}{2}-\frac{1}{3}+\frac{1}{3}-\frac{1}{4}+...+\frac{1}{2010}-\frac{1}{2011}\)
\(S=\frac{1}{1}-\frac{1}{2011}=\frac{2010}{2011}\)
Bài 2 :
\(S=\frac{1}{10}-\frac{1}{13}+\frac{1}{13}-\frac{1}{16}+\frac{1}{16}-\frac{1}{19}+...+\frac{1}{58}-\frac{1}{61}\)
\(S=\frac{1}{10}-\frac{1}{61}=\frac{51}{610}\)
Bài 3 :
\(3S=\frac{3}{4\times7}+\frac{3}{7\times11}+...+\frac{3}{19\times22}\)
\(3S=\frac{1}{4}-\frac{1}{7}+\frac{1}{7}-\frac{1}{11}+...+\frac{1}{19}-\frac{1}{22}\)
\(3S=\frac{1}{4}-\frac{1}{22}\)
\(S=\frac{18}{88}\div3=\frac{6}{88}\)
Đúng 0
Bình luận (0)