Chứng minh DB=DC, góc E bằng góc H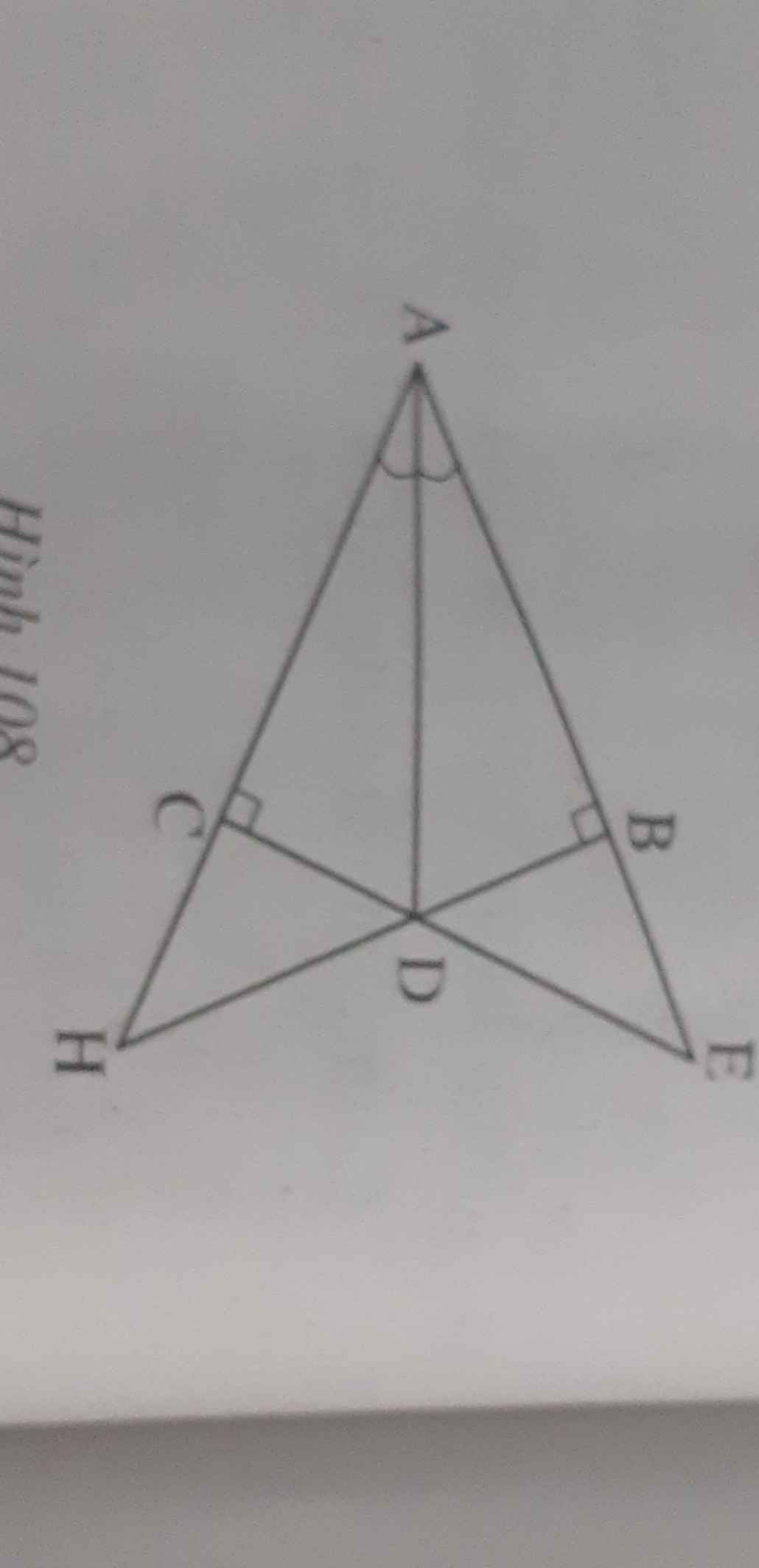
KM
Những câu hỏi liên quan
Cho tam giácABCcóAB + AC và A < 90. Tia phân giác của góc A cắt B Cở D .
a) Chứng minh rằng DB DC =
b) Chứng minh rằng AD vuông góc với BC .
c) Vẽ đoạn thẳng CE vuông góc và bằng CB (E khác phía A đối với CB ), Vẽ đoạn thẳng CF vuông góc và bằng CA (F khác phía B đối với CA ).Chứng minh rằng EA vuông góc FB.
b: Ta có: ΔACB cân tại A
mà AD là tia phân giác
nên AD là đường cao
Đúng 0
Bình luận (0)
CHO TAM GIÁC ABC CÂN TẠI A CÓ GÓC ABC 30 ĐỘ . KẺ AH VUÔNG GÓC VỚI BC TẠI H (H THUỘC ) . TRÊN ĐOẠN HC LẤY ĐIỂM D SAO CHO HD HB 1) CHỨNG MINH : AB AD 2) CHỨNG MINH : DA DB DC 3) TỪ C KẺ CE VUÔNG GÓC VỚI AD TẠI E , CHỨNG MINH HE SONG SONG VỚI AC MONG MN GIÚP MIK Ạ MIK ĐANG CẦN GẤP CẢM ƠN MN Ạ
Đọc tiếp
CHO TAM GIÁC ABC CÂN TẠI A CÓ GÓC ABC = 30 ĐỘ . KẺ AH VUÔNG GÓC VỚI BC TẠI H (H THUỘC ) . TRÊN ĐOẠN HC LẤY ĐIỂM D SAO CHO HD = HB
1) CHỨNG MINH : AB = AD
2) CHỨNG MINH : DA = DB = DC
3) TỪ C KẺ CE VUÔNG GÓC VỚI AD TẠI E , CHỨNG MINH HE SONG SONG VỚI AC
MONG MN GIÚP MIK Ạ MIK ĐANG CẦN GẤP CẢM ƠN MN Ạ ![]()
cho tam giác ABC ; góc A bằng 60độ; AB<AC vẽ đường cao BH; H thuộc AB
a, so sánh góc ABC và góc ACB. tính góc ABH
b, Vẽ AD là phân giác cyar góc A, D thuộc BC, vẽ BI vuông góc với AD tại I. chứng minh : tam giác AIB = tam giác BHA
c, vẽ BI cắt AC tại E chứng minh tam giác ABE đều
d, Chứng minh DC > DB
Cho tam giác ABC có góc A bằng 60°, đường cao BH ( H thuộc AC)
a, so sánh góc ABC và góc ACB. Tính góc ABH
b, vẽ AD là phân giác của góc A ( D thuộc BC), vẽ BI vuông góc với AD tại I. Chứng minh ∆ AIB=∆ BHA
c, tia BI cắt AC ở E. Chứng minh ∆ ABE đều
d, chứng minh DC > DB
GIÚP MÌNH CÂU D NHÉ !!!! MÌNH CẦN GẤP
Cho tam giác ABC có góc A=60 độ, AB<AC. Kẻ BH vuông góc với AC (H thuộc AC). AD là tia phân giác của góc A. BI vuông góc với AD tại I. BI cắt AC tại E. Chứng minh DC>DB
Cho tam giác ABC vuông tại A, góc ACB=30 độ. Kẻ AH vuông góc với BC tại H (H thuộc BC) . Trên đoạn HC lấy điểm D sao cho HD=HB.
a) Chứng minh AB=AD
b) Chứng minh DA=DB=DC
c) Từ C kẻ CE vuông góc với AD tại E. Chứng minh HE song song với AC
Cho ∆ABC có AB<AC, đường phân giác AD. Trên AC lấy điểm E sao cho AE=AB
a) chứng minh ∆ABD=∆AED
b) AB cắt ED tại K. Chứng minh góc KBD= góc DEC và BK = EC
c) Chứng minh DC>DB
a, Xét tam giác ABD và tam giác AED có
AD _ chung ; ^BAD = ^EAD ; AB = AE
Vậy tam giác ABD = tam giác AED (c.g.c)
b, Ta có ^BKD + ^BDK = ^ABD
mà ^ABD = ^AED ( 2 góc tương ứng )
mà ^AED = ^EDC + ^ECD
-> ^BKD + ^BDK = ^EDC + ^ECD -> ^KBD = ^DEC
Xét tam giác BDK và tam giác EDC có
^KBD = ^DEC ( cmt ) ; BD = ED ( 2 cạnh tương ứng ) ; ^BDK = ^EDC ( đ.đ)
Vậy tam giác BDK = tam giác EDC (g.c.g)
=> BK = EC ( 2 cạnh tương ứng )
c, Ta có BD = ED mà ED < DC do cạnh góc vuông nhỏ hơn cạnh huyền
=> BD < DC
Đúng 1
Bình luận (0)
Cho △ABC có AB < AC, góc B và góc C là góc nhọn, AH ⊥ BC tại H. Trên tia đối tia HA lấy điểm D. Chứng minh DB < DC.
Xét ΔABC có
HB,HC lần lượt là hình chiếu của AB,AC trên BC
AB<AC
Do đó: HB<HC
Xét ΔDBC có
HB,HC lần lượt là hình chiếu của DB,DC trên BC
HB<HC
Do đó: DB<DC
Đúng 0
Bình luận (0)
Cho hình chữ nhật ABCD (AD AB) . Hai đường chéo AC và BD cắt nhau tại O. Qua D kẻ đường thẳng vuông góc với BD cắt tia BC tại E .a) Chứng minh tam giác BDE đồng dạng với tam giácDCE .b) Kẻ CH vuông góc với DE tại H . Chứng minh rằng: 2 . DC CH DB . Từ đó tínhđộ dài CH biết AD 6cm ; AB 8cm.c) Gọi K là giao điểm của OE và HC . Chứng minh:HK /ODEK/EO, từ đó suy ra: K là trung điểm của HC .d) Chứng minh ba đường thẳng ,, OE. CD .BH đồng quy
Đọc tiếp
Cho hình chữ nhật ABCD (AD <AB) . Hai đường chéo AC và BD cắt nhau tại O. Qua D kẻ đường thẳng vuông góc với BD cắt tia BC tại E .
a) Chứng minh tam giác BDE đồng dạng với tam giácDCE .
b) Kẻ CH vuông góc với DE tại H . Chứng minh rằng: 2 . DC CH DB = . Từ đó tính
độ dài CH biết AD = 6cm ; AB = 8cm.
c) Gọi K là giao điểm của OE và HC . Chứng minh:
HK /OD=EK/EO, từ đó suy ra: K là trung điểm của HC .
d) Chứng minh ba đường thẳng ,, OE. CD .BH đồng quy
a: Xét ΔBDE vuông tại D và ΔDCE vuông tại C có
góc E chung
=>ΔBDE đồng dạng với ΔDCE
b: BD=căn 8^2+6^2=10cm
BE=10^2/6=100/6=50/3cm
EC=DC^2/BC=8^2/6=32/3cm
Xét ΔEBD có CH//BD
nên CH/BD=EC/EB
=>CH/10=32/50=16/25
=>CH=160/25=6,4cm
Đúng 0
Bình luận (0)


