Trong các số sau: 5895; 7950; 300; 57654; 6980; 8647; 6470; 8692; 20560; 8426; 8832
a) Tìm các số chia hết cho cả 2 và 5
b) Tìm các số chia hết cho cả 2 và 3
c) Tìm các số chia hết cho cả 2, 3 và 5
SC
Những câu hỏi liên quan
Bài 1/ Trong các số sau: 5895; 7950; 300; 57654; 6980; 8647; 6470; 8692; 20560; 8426; 8832a) Tìm các số chia hết cho cả 2 và 5b) Tìm các số chia hết cho cả 2 và 3c) Tìm các số chia hết cho cả 2, 3 và 5 Bài 2/Tính bằng cách hợp lí nhất:a) 34750:125 + 65250 : 125 b) 2424 : 8 : 3 Bài 3/ Tìm x biết:a) 58 x – 934 6722 b) 2005 + x 34 5337 c) 12 x 15 38880 Bài 4/ Một khu đất hình chữ nhật có diện tích là 5670m , có chiều rộng là 54 m. Xung quanh khu đất người ta trồng cây ă...
Đọc tiếp
Bài 1/ Trong các số sau: 5895; 7950; 300; 57654; 6980; 8647; 6470; 8692; 20560; 8426; 8832
a) Tìm các số chia hết cho cả 2 và 5
b) Tìm các số chia hết cho cả 2 và 3
c) Tìm các số chia hết cho cả 2, 3 và 5
Bài 2/Tính bằng cách hợp lí nhất:
a) 34750:125 + 65250 : 125 b) 2424 : 8 : 3
Bài 3/ Tìm x biết:
a) 58 x – 934 = 6722 b) 2005 + x 34 = 5337 c) 12 x 15 = 38880
Bài 4/ Một khu đất hình chữ nhật có diện tích là 5670m , có chiều rộng là 54 m. Xung quanh khu đất người ta trồng cây ăn quả, cứ cách 3 m trồng 1 cây. Hỏi trồng được tất cả bao nhiêu cây ăn quả?
Bài 5/ Tính giá trị biểu thức
a) 31980 : 156 + 3995 : 47 b) ( 14515 + 8125 : 125 ) : 324
Bài 6/ Một mảnh vườn hình bình hành có đáy 24m, chiều cao bằng đáy. Tính diện tích mảnh vườn.
Mọi người ai giúp được câu nào thì giúp mình với ạ
ìm số nguyên dương n thỏa mãn : 1! + 2! +3! + .....+n! = p^2 + q^2 + 5895 Trong đó p và q là 2 số nguyên tố . quy ước rằng n! = 1 . 2 . 3 . 4 . .... . n
fth8457+5895=
ìm số nguyên dương n thỏa mãn : 1! + 2! +3! + .....+n! = p^2 + q^2 + 5895 Trong đó p và q là 2 số nguyên tố . quy ước rằng n! = 1 . 2 . 3 . 4 . .... . n
Ta thấy 1! + 2! = 3 \(⋮\) 3, còn từ 3! trở đi đương nhiên đều chia hết cho 3.
Do đó p2 + q2 + 5895 \(⋮\) 3. Mà 5895 \(⋮\) 3 nên p2 + q2 \(⋮\) 3 (1).
Lại có: p2 và q2 chia cho 3 dư 0 hoặc dư 1 do chúng đều là số chính phương (2).
Từ (1) và (2) \(\Rightarrow\) p2 \(⋮\) 3 và q2 \(⋮\) 3 \(\Rightarrow\) p \(⋮\) 3 và q \(⋮\) 3. Mà p và q là các snt nên p = q = 3 \(\Rightarrow\) 1! + 2! + 3! + ... + n! = 5913.
Vì n! < 5913 nên n < 8 \(\Rightarrow\) n \(\in\) {1; 2; 3; 4; 5; 6; 7}. Thử n với các số đó ta chỉ có n = 7 thỏa mãn.
Vậy n = 7.
Đúng 0
Bình luận (1)
Tích hai số là 5895.Nếu xóa chữ số 7 ở bên phải số bé và thêm số 5 vào bên trái số bé thì ta được số lớn.Tìm hai số đó.
Tìm tất cả các số nguyên dương n biết :
1!+2!+3!+...+n!= p ^2 +q^2 + 5895
p , q là 2 số nguyên tố .
Lưu ý đọc kĩ đề cho là tìm tất cả các số nhé ! Nếu chỉ có 1 số thì hãy giải thích luôn
Tớ làm đây r mà bạn:
Câu hỏi của Lev Ivanovich Yashin - Toán lớp 6 | Học trực tuyến
Đúng 0
Bình luận (0)
Lời giải:
Vì \(1!+2!+3!+...+n!=p^2+q^2+5895>5895\)
\(\Rightarrow n>3\)
Ta thấy mọi số \(x\in\mathbb{N}; x\geq 3\) thì \(x!\vdots 3\)
Do đó: \(3!\vdots 3; 4!\vdots 3;....; n!\vdots 3\). Mà \(1!+2!=3\vdots 3\)
\(\Rightarrow 1!+2!+...+n!\vdots 3\)
\(\Rightarrow p^2+q^2+5895\vdots 3\)
\(\Rightarrow p^2+q^2\vdots 3\)
Ta biết rằng, một số chính phương thì chia $3$ chỉ có dư $0$ hoặc $1$. +)Nếu $p,q$ đều không chia hết cho $3$
\(\Rightarrow p^2+q^2=3k+1+3t+1=3(t+k)+2\not\vdots 3\) (vô lý)
+) Nếu $p,q$ có một số chia hết cho $3$, một số không chia hết cho $3$ thì:
\(p^2+q^2=3t+3k+1=3(t+k)+1\not\vdots 3\) (vô lý)
Do đó chỉ còn TH $p,q$ đều chia hết cho $3$
Mà $p,q$ là số nguyên tố nên \(p=q=3\)
\(\Rightarrow 1!+2!+...+n!=3^2+3^2+5895=5913\)
Đến đây dùng phép thử ta thu được $n=7$ thỏa mãn.
Đúng 0
Bình luận (1)
1)trong các phân số sau,phân số nào tối giản : 14/-35;9/34;-10/48;-12/55
2)chỉ ra các phân số tối giản trong các phân số sau;1/4;-2/10;6/-9;13/-14;-14/-21;20/50
`1)9/34` và `(-12)/55`
`2)1/4` và `13/(-14)`
Đúng 1
Bình luận (0)
1) Các phân số tối giản là \(-\dfrac{9}{34}\) và \(-\dfrac{12}{55}\) vì đây là các phân số không rút gọn được nữa
2) Các phân số tối giản là \(\dfrac{13}{-14}\)
Đúng 0
Bình luận (1)
Trong các phân số sau đây, tìm phân số không bằng phân số nào trong các phân số còn lại:
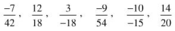
Rút gọn các phân số về phân số tối giản, sau đó so sánh để tìm ra phân số không bằng các phân số còn lại.
Ta rút gọn các phân số về dạng tối giản:
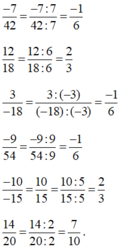
Do vậy ta có: 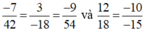
Phân số 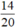 không bằng phân số nào trong các phân số còn lại.
không bằng phân số nào trong các phân số còn lại.
Đúng 0
Bình luận (0)
1. Xác định số oxi hóa củaa. Cl trong các chất sau: Cl2, HCl, HClO, HClO2, HClO3, HClO4, ClO4-, MgCl2b. S trong các chất sau: S, Na2S, SO2, SO3, H2SO3, H2SO4, K2SO4c. N trong các chất sau: N2, N2O, NO, NO2, HNO3, NH4Cl, NH4NO3d. Mn trong các chất sau: MnO2, KMnO4, K2MnO4, MnO4-, Mn(OH)2e. Cr trong các chất sau: Cr2O3, K2CrO4, K2Cr2O7, Cr2O72-, CrCl3f. Fe trong các chất sau: Fe, FeO, Fe2O3, Fe3O4, FeS, FeCl2, FeCl3, FeCO3, FeSO4, Fe2(SO4)3, Fe3+g. C trong các hợp chất sau: CO, CO2, Na2CO3, CH4, C...
Đọc tiếp
1. Xác định số oxi hóa của
a. Cl trong các chất sau: Cl2, HCl, HClO, HClO2, HClO3, HClO4, ClO4-, MgCl2
b. S trong các chất sau: S, Na2S, SO2, SO3, H2SO3, H2SO4, K2SO4
c. N trong các chất sau: N2, N2O, NO, NO2, HNO3, NH4Cl, NH4NO3
d. Mn trong các chất sau: MnO2, KMnO4, K2MnO4, MnO4-, Mn(OH)2
e. Cr trong các chất sau: Cr2O3, K2CrO4, K2Cr2O7, Cr2O72-, CrCl3
f. Fe trong các chất sau: Fe, FeO, Fe2O3, Fe3O4, FeS, FeCl2, FeCl3, FeCO3, FeSO4, Fe2(SO4)3, Fe3+
g. C trong các hợp chất sau: CO, CO2, Na2CO3, CH4, C2H4, C2H2, C2H5OH






