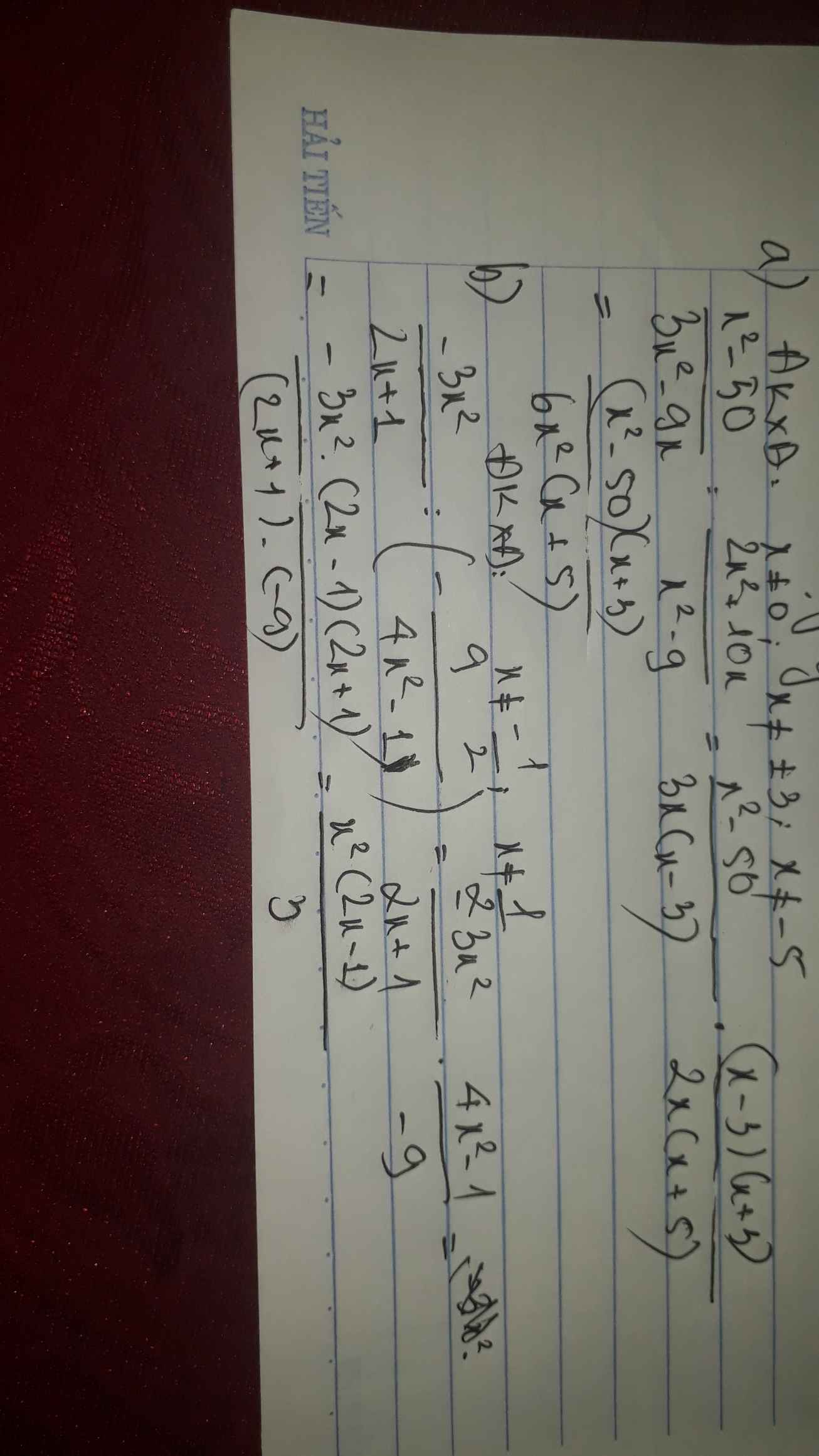a) \(\dfrac{1}{3x-2}-\dfrac{1}{3x+2}-\dfrac{3x-6}{9x^2-4}\)

\(=\dfrac{3x+2-3x+2-3x+6}{\left(3x-2\right)\left(3x+2\right)}\)

\(=\dfrac{-3x+10}{\left(3x-2\right)\left(3x+2\right)}\)

b) \(\dfrac{x+25}{2x^2-50}-\dfrac{x+5}{x^2-5x}-\dfrac{5-x}{2x^2+10x}\)

\(=\dfrac{x+25}{2\left(x-5\right)\left(x+5\right)}-\dfrac{x+5}{x\left(x-5\right)}+\dfrac{x-5}{2x\left(x+5\right)}\)

\(=\dfrac{x^2+25x-2\left(x+5\right)^2+\left(x-5\right)^2}{2x\left(x-5\right)\left(x+5\right)}\)

\(=\dfrac{x^2+25x-2x^2-20x-50+x^2-10x+25}{2x\left(x-5\right)\left(x+5\right)}\)

\(=\dfrac{-5x-25}{2x\left(x-5\right)\left(x+5\right)}\)

\(=\dfrac{-5\left(x+5\right)}{2x\left(x-5\right)\left(x+5\right)}=\dfrac{-5}{2x\left(x-5\right)}\)

c) Ta có: \(\dfrac{1-2x}{2x}-\dfrac{4x}{2x-1}-\dfrac{3}{2x-4x^2}\)

\(=\dfrac{-\left(2x-1\right)^2-8x^2+3}{2x\left(2x-1\right)}\)

\(=\dfrac{-\left(4x^2-4x+1\right)-8x^2+3}{2x\left(2x-1\right)}\)

\(=\dfrac{-4x^2+4x-1-8x^2+3}{2x\left(2x-1\right)}\)

\(=\dfrac{-12x^2+4x+2}{2x\left(2x-1\right)}\)

a) ĐKXĐ: \(x\notin\left\{-1;-2;2\right\}\)

Ta có: \(\dfrac{1}{x^2+3x+2}-\dfrac{3}{x^2-x-2}=\dfrac{-1}{x^2-4}\)

\(\Leftrightarrow\dfrac{1}{\left(x+1\right)\left(x+2\right)}-\dfrac{3}{\left(x-2\right)\left(x+1\right)}=\dfrac{-1}{\left(x-2\right)\left(x+2\right)}\)

\(\Leftrightarrow\dfrac{x-2}{\left(x+1\right)\left(x+2\right)\left(x-2\right)}-\dfrac{3\left(x+2\right)}{\left(x+2\right)\left(x+1\right)\left(x-2\right)}=\dfrac{-1\left(x+1\right)}{\left(x+1\right)\left(x-2\right)\left(x+2\right)}\)

Suy ra: \(x-2-3x-6=-x-1\)

\(\Leftrightarrow-2x-8+x+1=0\)

\(\Leftrightarrow-x-7=0\)

\(\Leftrightarrow-x=7\)

hay x=-7(thỏa ĐK)

Vậy: S={-7}

a) ĐKXĐ: 

Ta có: ⇔1(x+1)(x+2)−3(x−2)(x+1)=−1(x−2)(x+2)⇔1(x+1)(x+2)−3(x−2)(x+1)=−1(x−2)(x+2)

⇔x−2(x+1)(x+2)(x−2)−3(x+2)(x+2)(x+1)(x−2)=−1(x+1)(x+1)(x−2)(x+2)⇔x−2(x+1)(x+2)(x−2)−3(x+2)(x+2)(x+1)(x−2)=−1(x+1)(x+1)(x−2)(x+2)

Suy ra: 

hay x=-7(thỏa ĐK)

Vậy: S={-7}

Đọc tiếp

c: =>\(\dfrac{2x-1}{\left(x+5\right)\left(x-1\right)}+\dfrac{x-2}{\left(x-1\right)\left(x-9\right)}=\dfrac{3x-12}{\left(x-9\right)\left(x+5\right)}\)

=>(2x-1)(x-9)+(x-2)(x+5)=(3x-12)(x-1)

=>2x^2-19x+9+x^2+3x-10=3x^2-15x+12

=>-16x-1=-15x+12

=>-x=13

=>x=-13

\(\dfrac{x^2-50}{3x^2-9x}\div\dfrac{2x^2+10x}{x^2-9}\)

\(\Leftrightarrow\dfrac{x^2-50}{3x\left(x-3\right)}\div\dfrac{2x^2+10x}{\left(x-3\right)\left(x+3\right)}\)

MTC: 3x(x-3)(x+3)

\(\dfrac{(x^2-50)\left(x+3\right)}{3x\left(x-3\right)\left(x+3\right)}\div\dfrac{3x(2x^2+10x)}{3x\left(x-3\right)\left(x+3\right)}\)

\(\Rightarrow\)(x²-50)(x+3):3x(2x²+10x)

\(\Rightarrow\)(x³+3x²-50x-150):6x³+30x²

a) Ta có: \(\dfrac{x^2-50}{3x^2-9x}:\dfrac{2x^2+10x}{x^2-9}\)

\(=\dfrac{x^2-50}{3x\left(x-3\right)}\cdot\dfrac{\left(x-3\right)\left(x+3\right)}{2x\left(x+5\right)}\)

\(=\dfrac{\left(x^2-50\right)\left(x+3\right)}{6x^2\left(x+5\right)}\)

b) Ta có: \(\dfrac{-3x^2}{2x+1}:\dfrac{-9}{4x^2-1}\)

\(=\dfrac{3x^2}{2x+1}\cdot\dfrac{\left(2x+1\right)\left(2x-1\right)}{9}\)

\(=\dfrac{x^2\left(2x-1\right)}{3}\)

1.

\(-4\le\dfrac{x^2-2x-7}{x^2+1}\le1\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-2x-7\le x^2+1\\-4x^2-4\le x^2-2x-7\end{matrix}\right.\) (Do \(x^2+1>0\))

\(\Leftrightarrow\left\{{}\begin{matrix}x\ge-4\\\left[{}\begin{matrix}x\ge1\\x\le-\dfrac{3}{5}\end{matrix}\right.\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}x\ge1\\-4\le x\le-\dfrac{3}{5}\end{matrix}\right.\)

2.

\(\dfrac{1}{13}\le\dfrac{x^2-2x-2}{x^2-5x+7}\le1\)

\(\Leftrightarrow\left\{{}\begin{matrix}x^2-5x+7\le13x^2-26x-26\\x^2-2x-2\le x^2-5x+7\end{matrix}\right.\) (Do \(x^2-5x+7>0\))

\(\Leftrightarrow\left\{{}\begin{matrix}\left[{}\begin{matrix}x\ge\dfrac{11}{4}\\x\le-1\end{matrix}\right.\\x\le3\end{matrix}\right.\)

\(\Leftrightarrow\left[{}\begin{matrix}\dfrac{11}{4}\le x\le3\\x\le-1\end{matrix}\right.\)

câu d

\(D=\dfrac{\left(1-x^2\right)}{x}\left(\dfrac{x^2}{x+3}-1\right)+\dfrac{3x^2-14x+3}{x^2+3x}\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\left\{-3;0\right\}\\D=\dfrac{\left(1-x^2\right)\left(x^2-x-3\right)+3x^2-14x+3}{x\left(x+3\right)}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\left\{-3;0\right\}\\D=\dfrac{x^2-x-3-x^4+x^3-3x^2+3x^2-14x+3}{x\left(x+3\right)}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\left\{-3;0\right\}\\D=\dfrac{-x^4+x^3+x^2-15x}{x\left(x+3\right)}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\left\{-3;0\right\}\\D=\dfrac{-x\left(x^3-x^2-x+15\right)}{x\left(x+3\right)}\end{matrix}\right.\)

\(\Leftrightarrow\left\{{}\begin{matrix}x\ne\left\{-3;0\right\}\\D=\dfrac{-\left(x^3-x^2-x+15\right)}{\left(x+3\right)}\end{matrix}\right.\)

a) Ta có: \(\left(\dfrac{1}{x^2+x}-\dfrac{2-x}{x+1}\right):\left(\dfrac{1}{x}+x-2\right)\)

\(=\left(\dfrac{1}{x\left(x+1\right)}+\dfrac{x+2}{x+1}\right):\left(\dfrac{1}{x}+x-2\right)\)

\(=\dfrac{x^2+2x+1}{x\left(x+1\right)}:\dfrac{x^2-2x+1}{x}\)

\(=\dfrac{\left(x+1\right)^2}{x\left(x+1\right)}\cdot\dfrac{x}{\left(x-1\right)^2}\)

\(=\dfrac{x+1}{\left(x-1\right)^2}\)

b) Ta có: \(\left(\dfrac{3x}{1-3x}+\dfrac{2x}{3x+1}\right):\dfrac{6x^2+10x}{1-6x+9x^2}\)

\(=\dfrac{3x\left(3x+1\right)+2x\left(1-3x\right)}{\left(1-3x\right)\left(1+3x\right)}:\dfrac{2x\left(3x+5\right)}{\left(1-3x\right)^2}\)

\(=\dfrac{9x^2+3x+2x-6x^2}{\left(1-3x\right)\left(1+3x\right)}:\dfrac{2x\left(3x+5\right)}{\left(1-3x\right)^2}\)

\(=\dfrac{3x^2+5x}{\left(1-3x\right)\left(1+3x\right)}\cdot\dfrac{\left(1-3x\right)^2}{2x\left(3x+5\right)}\)

\(=\dfrac{x\left(3x+5\right)}{1+3x}\cdot\dfrac{1-3x}{2x\left(3x+5\right)}\)

\(=\dfrac{2\left(1-3x\right)}{3x+1}\)

c) Ta có: \(\left(\dfrac{9}{x^3-9x}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x^2+3x}-\dfrac{x}{3x+9}\right)\)

\(=\left(\dfrac{9}{x\left(x-3\right)\left(x+3\right)}+\dfrac{1}{x+3}\right):\left(\dfrac{x-3}{x\left(x+3\right)}-\dfrac{x}{3\left(x+3\right)}\right)\)

\(=\dfrac{9+x\left(x-3\right)}{x\left(x-3\right)\left(x+3\right)}:\dfrac{3\left(x-3\right)-x^2}{3x\left(x+3\right)}\)

\(=\dfrac{9+x^2-3x}{x\left(x-3\right)\left(x+3\right)}\cdot\dfrac{3x\left(x+3\right)}{3x-9-x^2}\)

\(=\dfrac{x^2-3x+9}{x-3}\cdot\dfrac{3}{-\left(x^2-3x+9\right)}\)

\(=\dfrac{-3}{x-3}\)